核函数

Posted 2021-01-03 shensobaolibin

通过支持向量机，我们可以发现

支持向量机能很好的将两个线性可分的样本分开

那么对于不是线性可分的样本，我们就要通过核函数去处理他了

 

也就是说，核函数的做用就是将线性不可分的样本，通过核函数印射到另外一个空间中

是样本变成线性可分的

 

那么常用的核函数有两种

一种是线性核函数

也就是直接x‘ = w * x + b

这样子一般是对线性可分的样本做这个核函数

 

那对于线性不可分的样本，我们一般是做高斯核函数

高斯核函数表示的是与某个点的相似程度

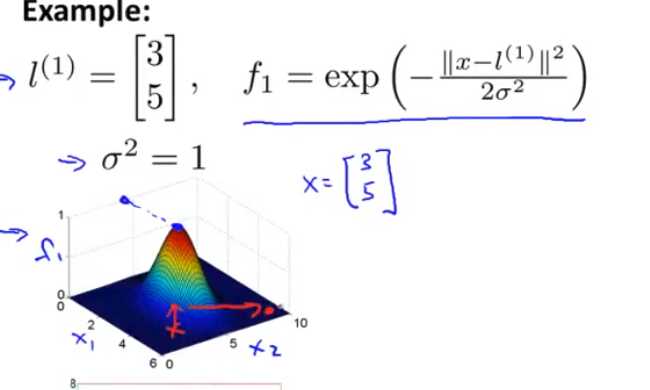
l就是这个点

也就是说，将点输入一个高斯核函数只会得到一个值

如果我们有n个高斯核，那么我们之前的点就会变成一个n维空间中的点

然后在高维空间中就是线性可分的了

 

那么对与一个高斯核来说，我们要选择的东西有两个，一个是l，一个是alaph

对于支持向量机来说

我们要选择有多少个高斯核

 

首先，对于多少个高斯核

如果我们的数据量比数据的维数大很多的话，我们高斯核就应该选择的多一些

因为这种情况允许我们得到一个复杂的比较准确的边界情况

 

如果数据量较小，数据维数较大，我们通过训练数据如果使用多个高斯核则特别容易产生过拟合

这时候就只能用少量的高斯核了

 

然后再说l

我们订好了要选n个高斯核

那么我们就从样本集中随机选n个作为高斯核的l

保证分布的平均

这样可以把样本分为一类一类的，相当于做了一个简单的小聚类

然后点离各种聚类的距离通过加权计算(SVM)即可得到正确的解

 

最后说alaph

如果alaph过大那么在距离l很远的点，这个核函数都会有较大的返回值

这样的话可能误差较大(因为特征不明显)，方差较小

 

若alaph过小那么只有离l很近的点核函数才会有返回值

这样可能方差较大(特征明显易过拟合)，误差较小