机器学习 多项式回归与模型泛化(上)

Posted 2021-01-03 zhangtaotqy

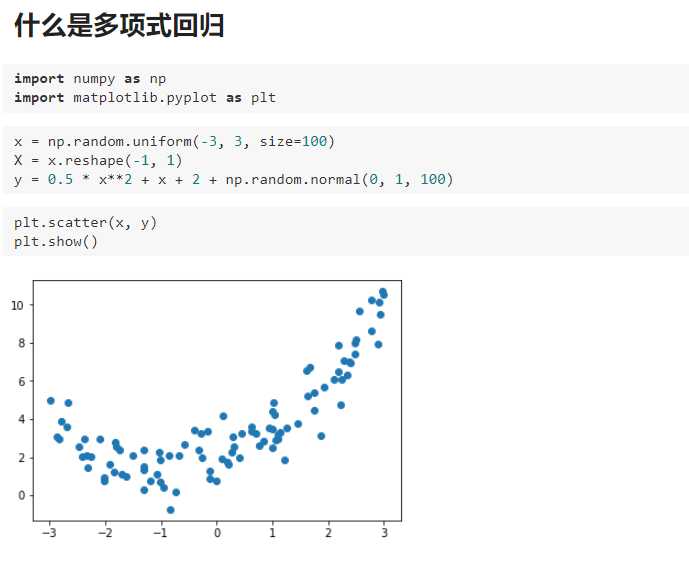
一、什么是多项式回归

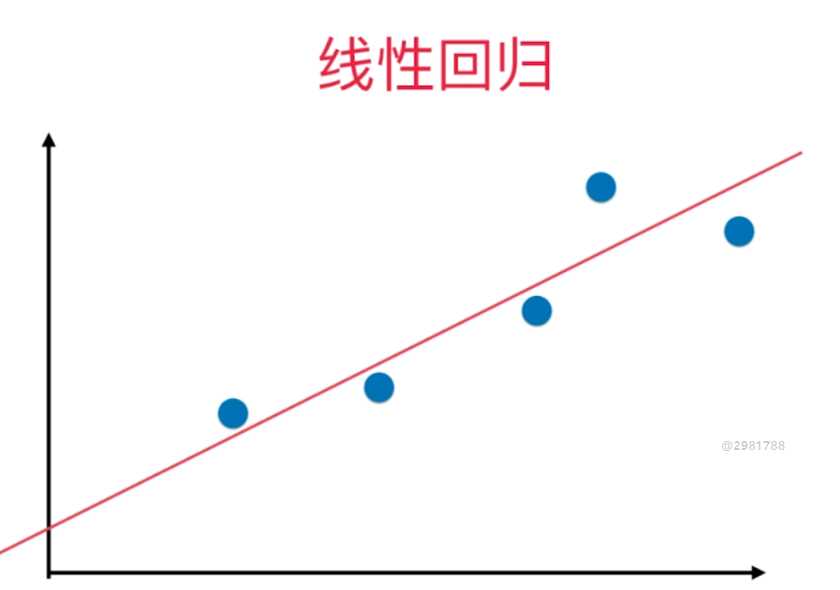
直线回归研究的是一个依变量与一个自变量之间的回归问题，但是，在畜禽、水产科学领域的许多实际问题中，影响依变量的自变量往往不止一个，而是多个，比如绵羊的产毛量这一变量同时受到绵羊体重、胸围、体长等多个变量的影响，因此需要进行一个依变量与多个自变量间的回归分析，即多元回归分析。

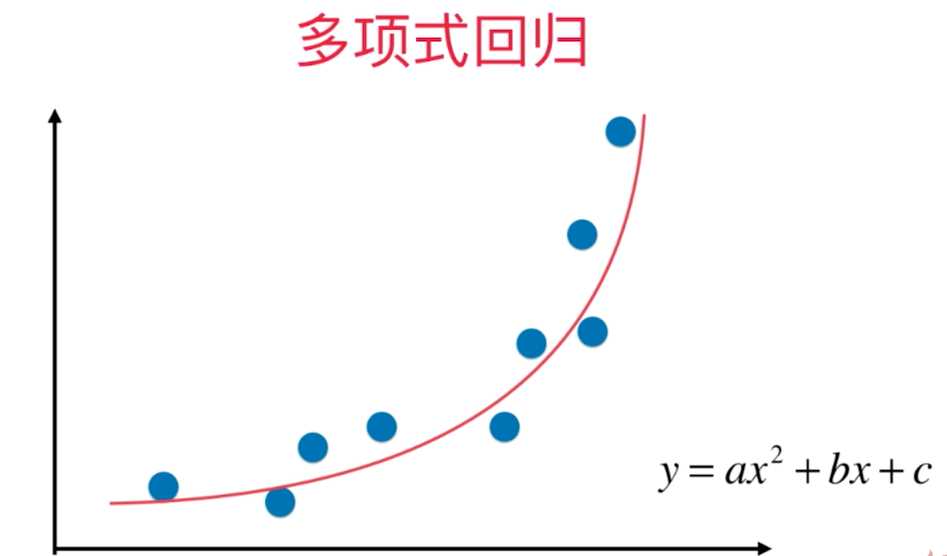
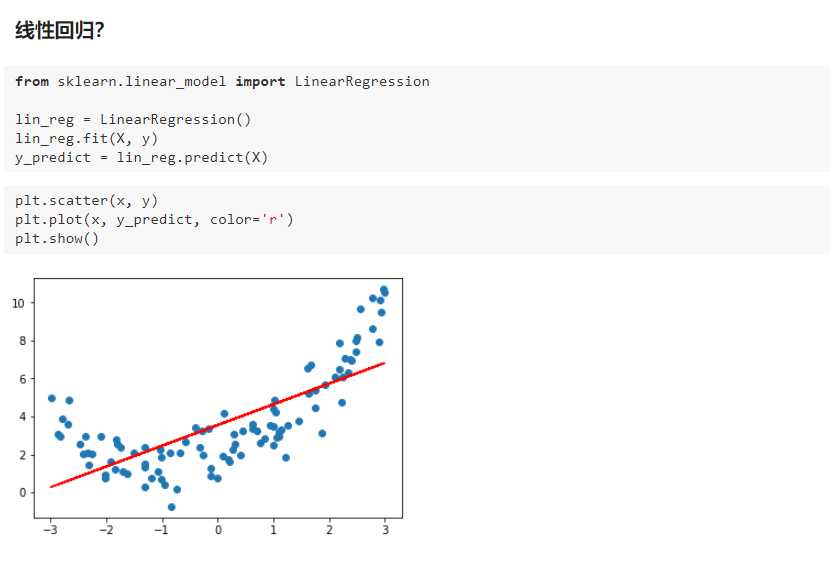
研究一个因变量与一个或多个自变量间多项式的回归分析方法，称为多项式回归（Polynomial Regression）。如果自变量只有一个时，称为一元多项式回归；如果自变量有多个时，称为多元多项式回归。在一元回归分析中，如果依变量y与自变量x的关系为非线性的，但是又找不到适当的函数曲线来拟合，则可以采用一元多项式回归。

一元m次多项式回归方程为：

  

。

二元二次多项式回归方程为：

  

。

多项式回归的最大优点就是可以通过增加x的高次项对实测点进行逼近，直至满意为止。事实上，多项式回归可以处理相当一类非线性问题，它在回归分析中占有重要的地位，因为任一函数都可以分段用多项式来逼近。因此，在通常的实际问题中，不论依变量与其他自变量的关系如何，我们总可以用多项式回归来进行分析。

多项式回归问题可以通过变量转换化为多元线性回归问题来解决。

对于一元m次多项式回归方程，令

  

，则该一元m次多项式就转化为m元线性回归方程

  

。因此用多元线性函数的回归方法就可解决多项式回归问题。需要指出的是，在多项式回归分析中，检验回归系数

  

是否显著，实质上就是判断自变量x的i次方项

  

对依变量y的影响是否显著。

对于二元二次多项式回归方程，令

  

，则该二元二次多项式函数就转化为五元线性回归方程

  

。但随着自变量个数的增加,多元多项式回归分析的计算量急剧增加。多元多项式回归属于多元非线性回归问题。 [2] 

模型如以下形式的称为一元多项式回归模型：

 

 

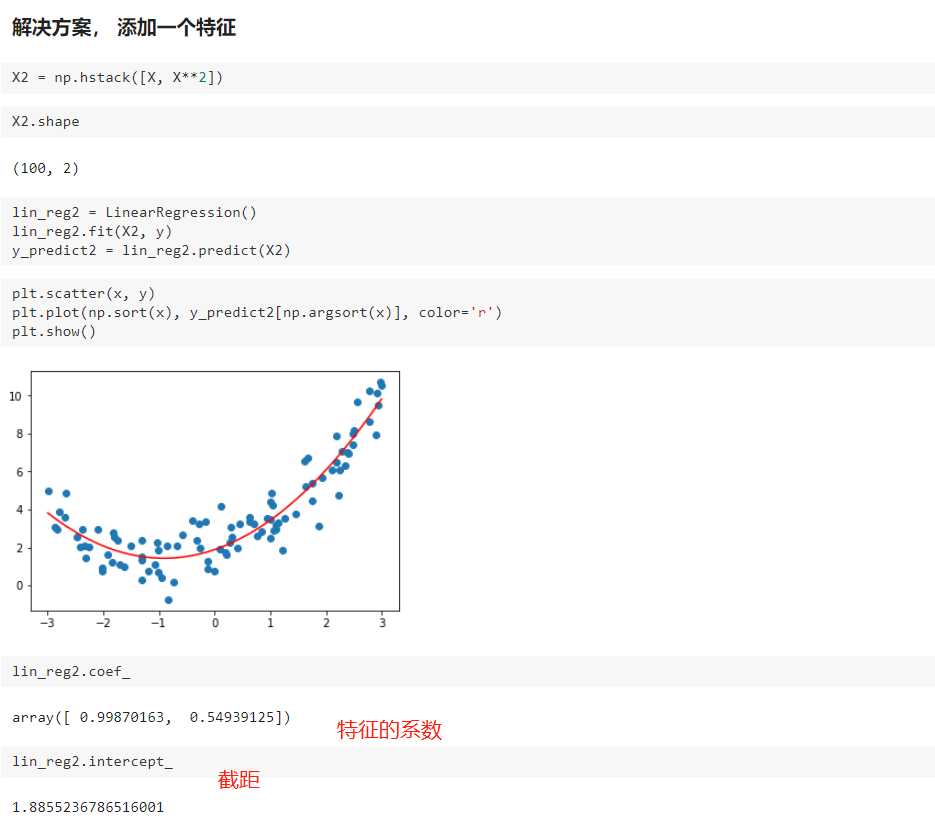
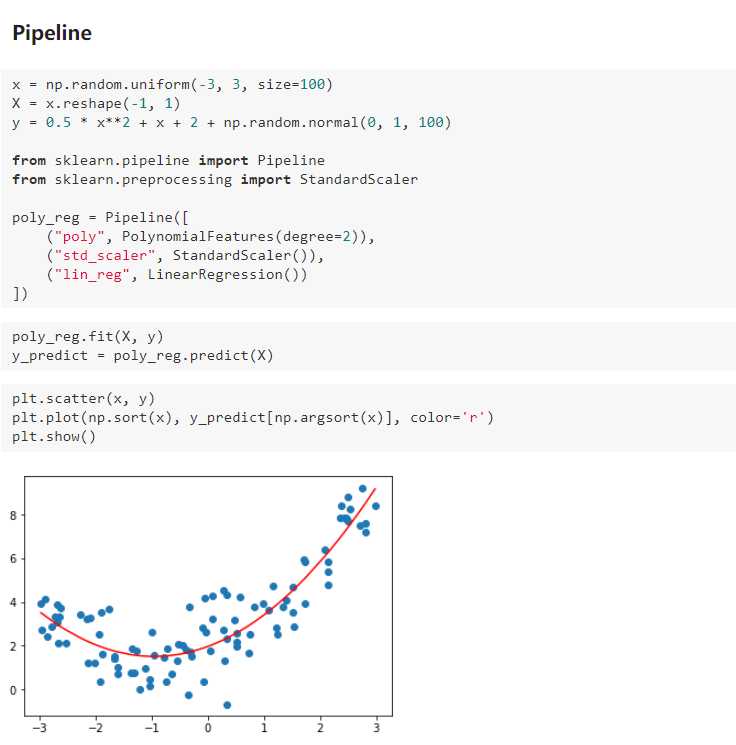
二、scikit-learn中的多项式回归与Pipeline

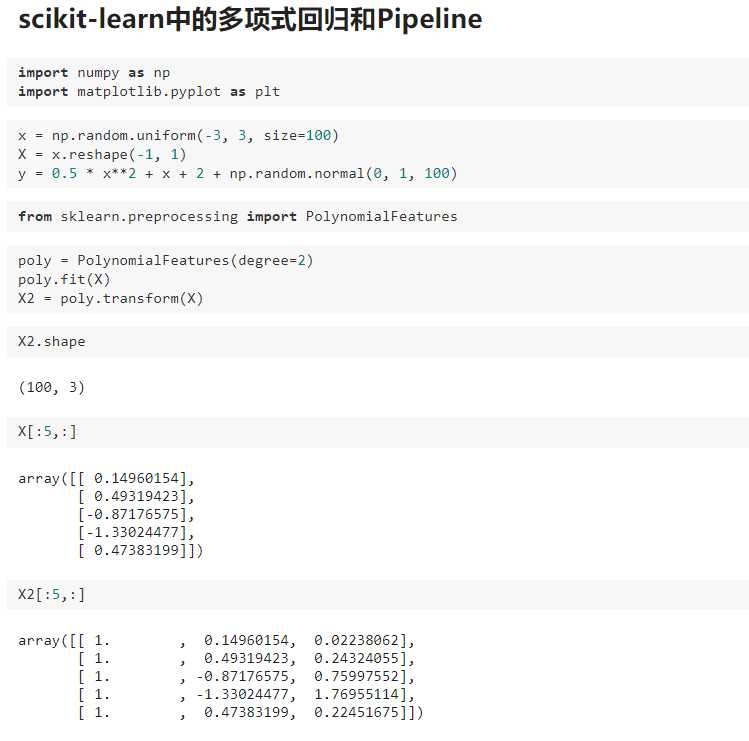
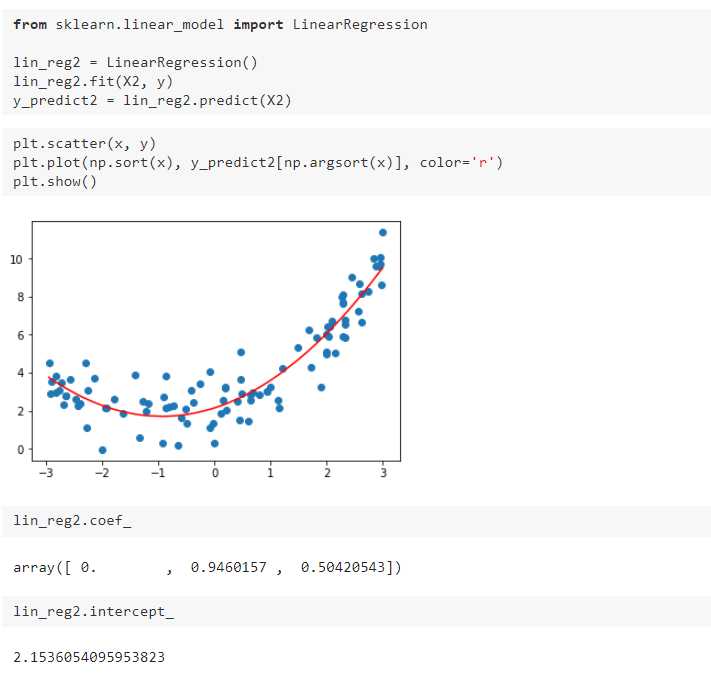
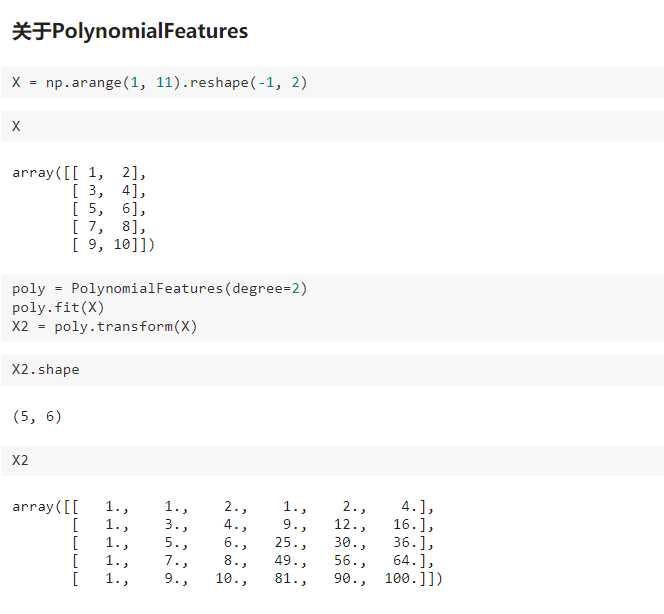
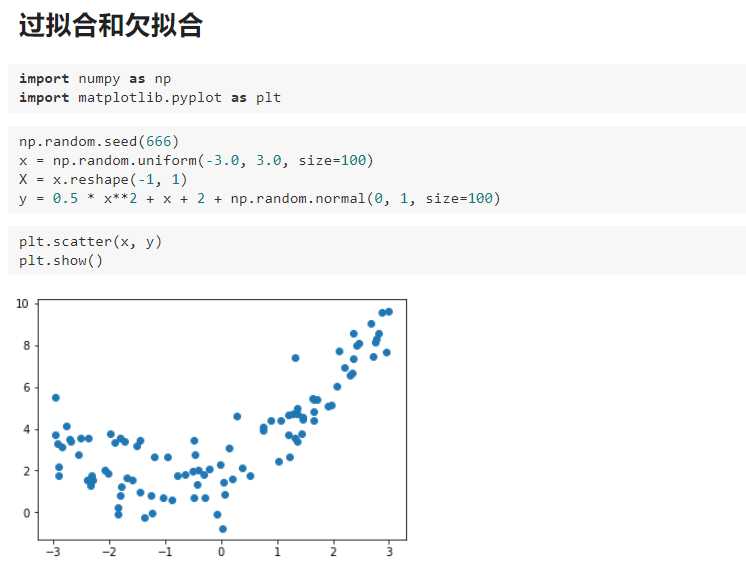
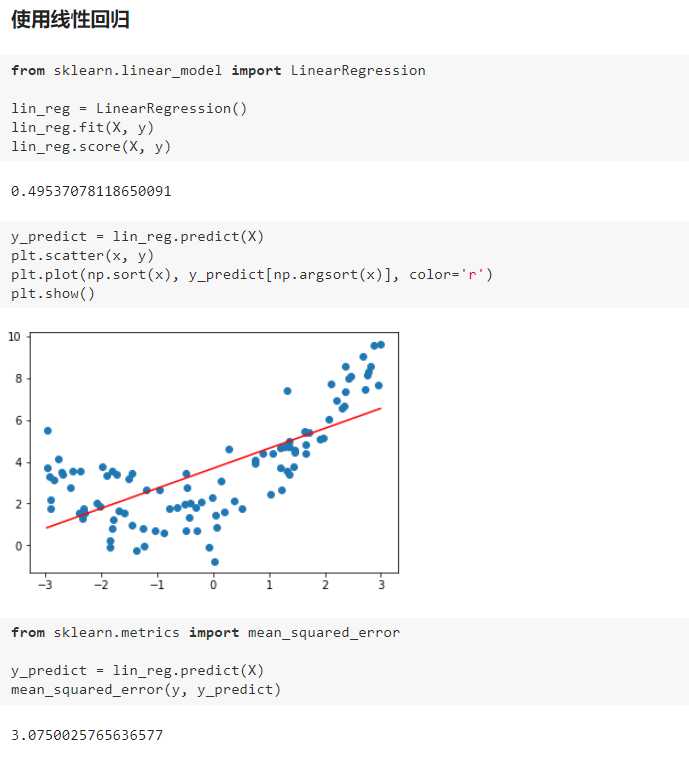
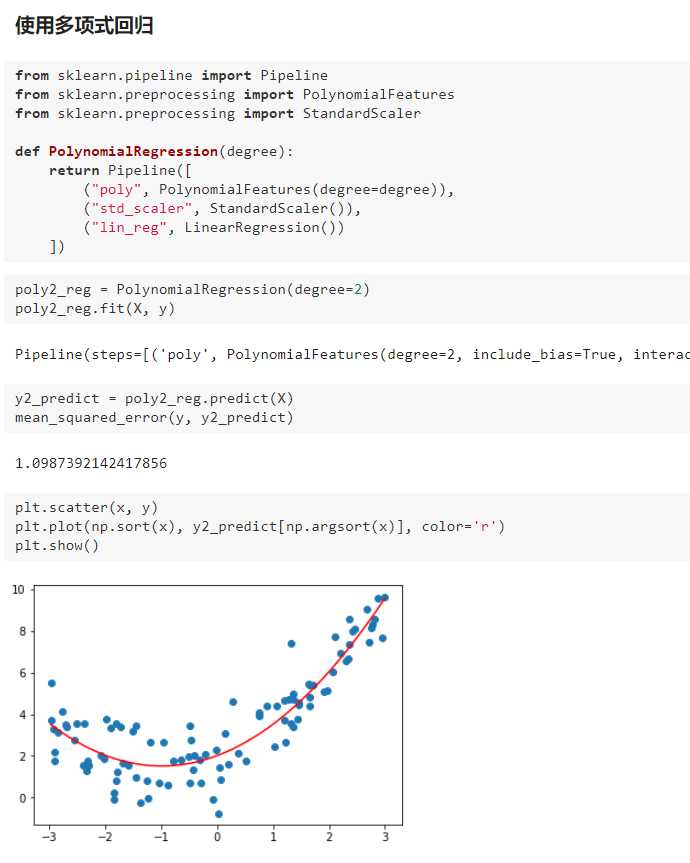
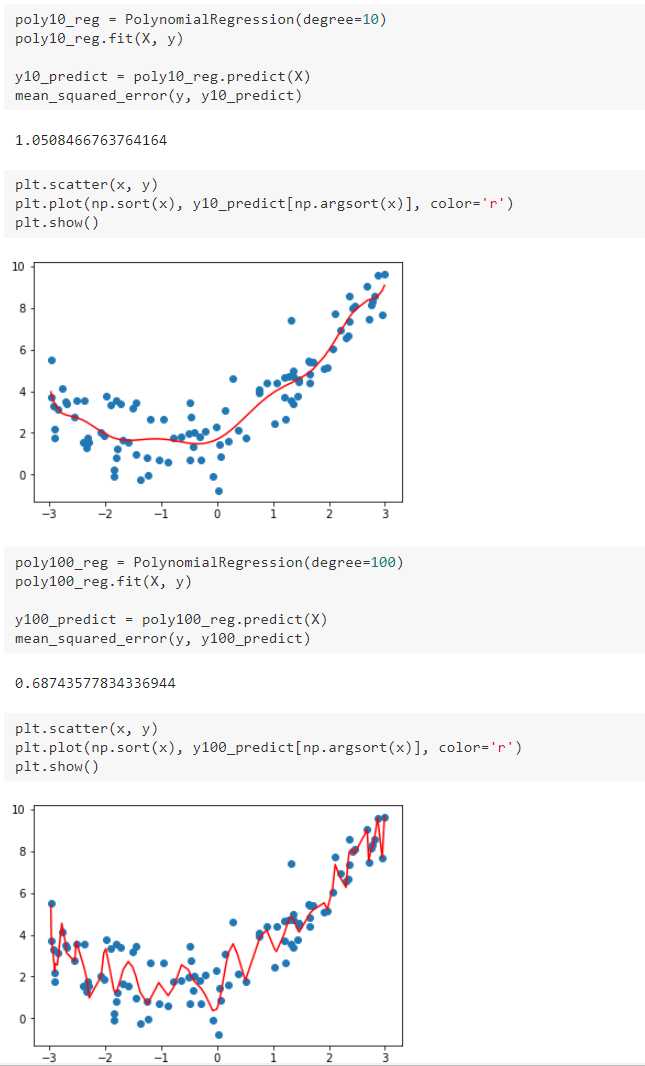
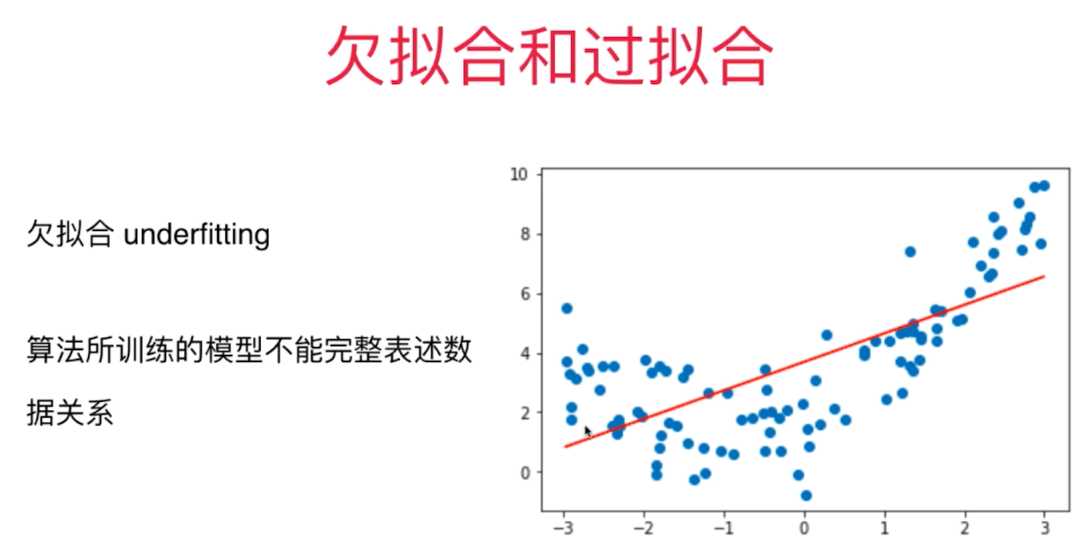
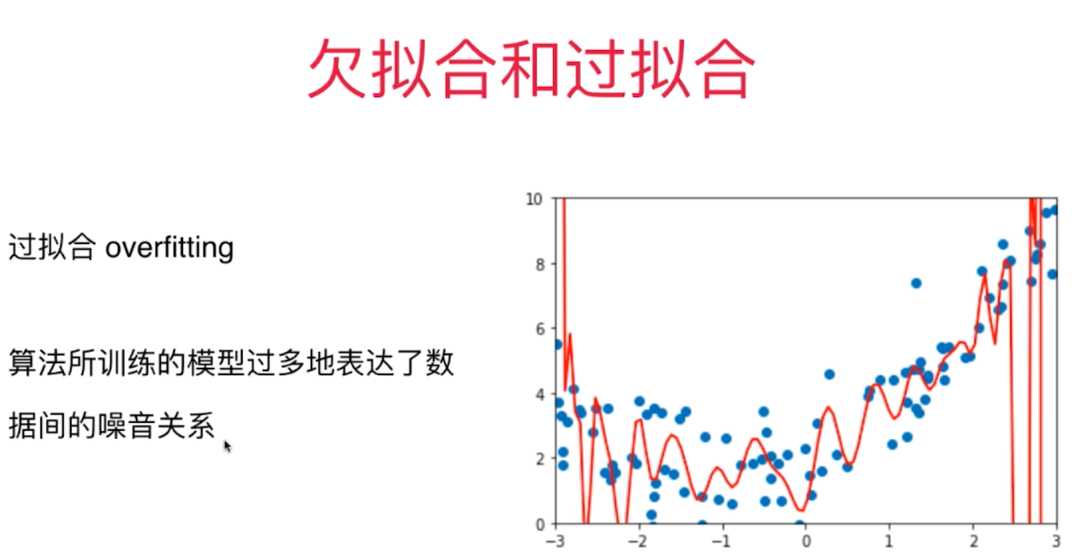
三、过拟合与欠拟合

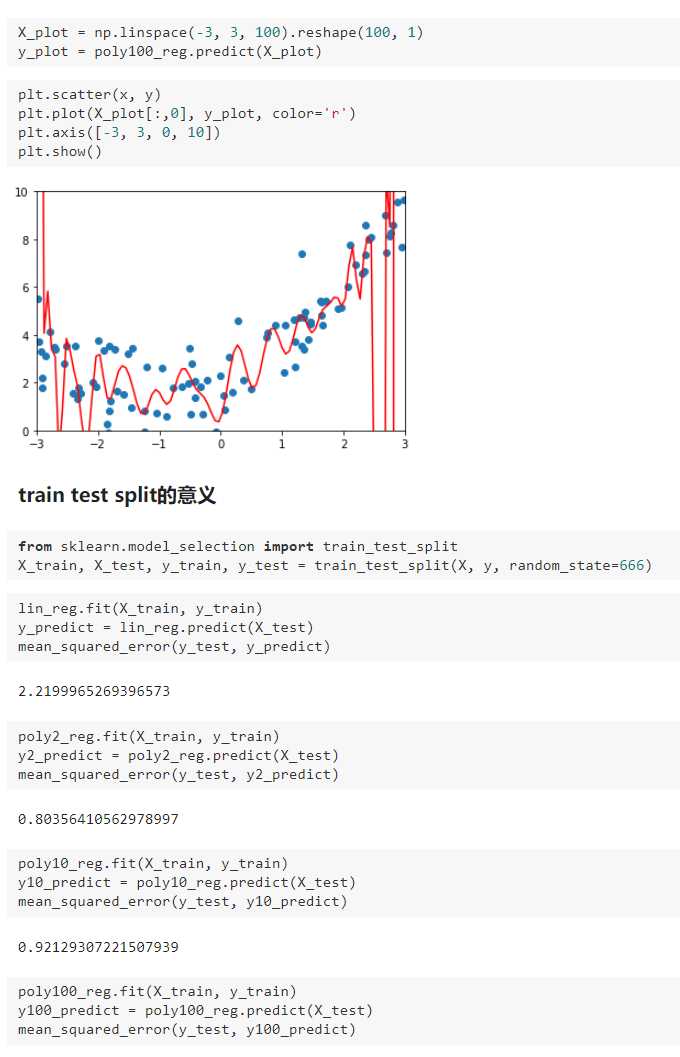
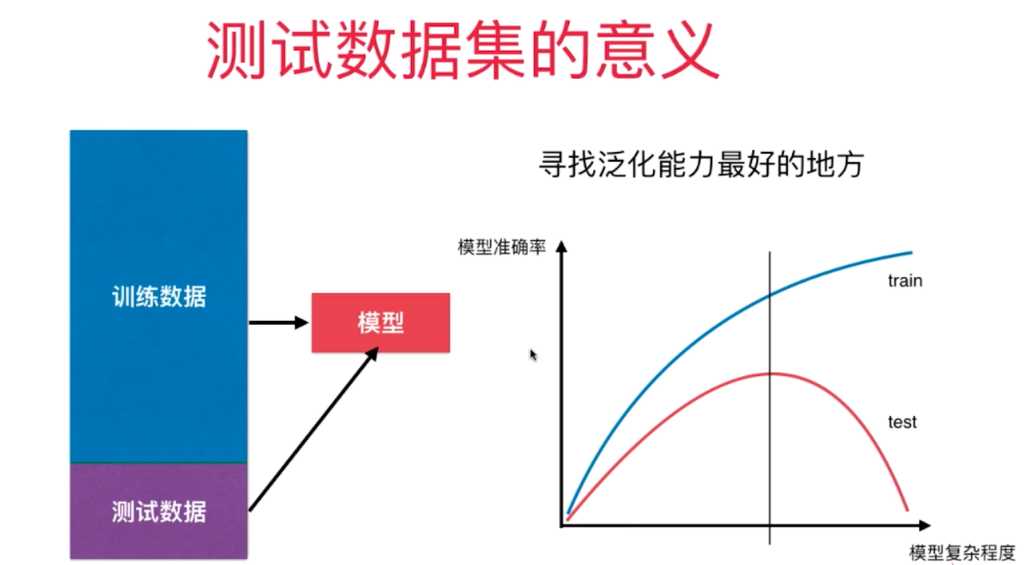
四、为什么要有训练数据集与测试数据集

 

 

 

 

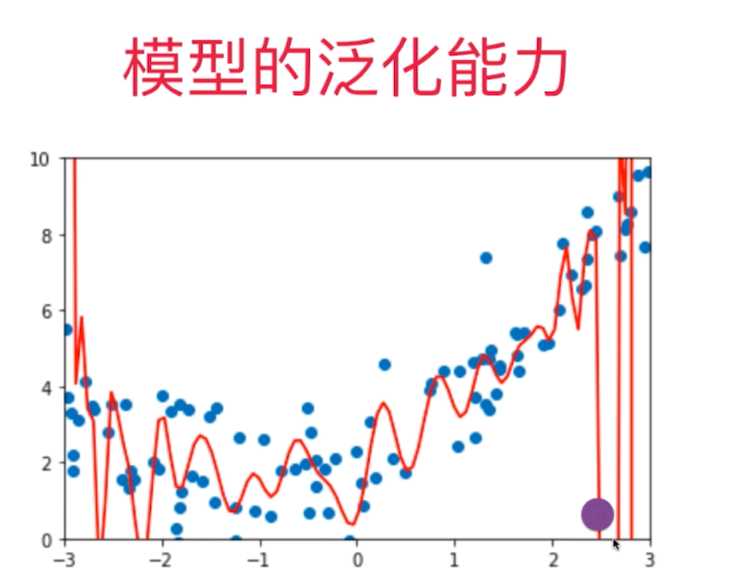
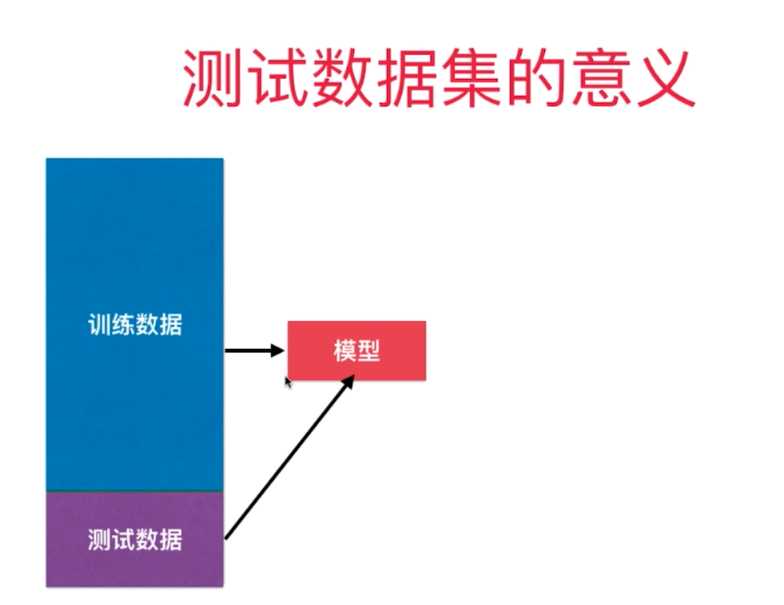
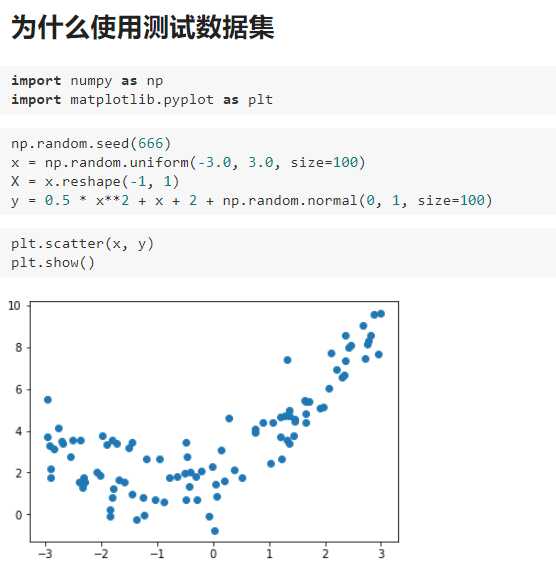
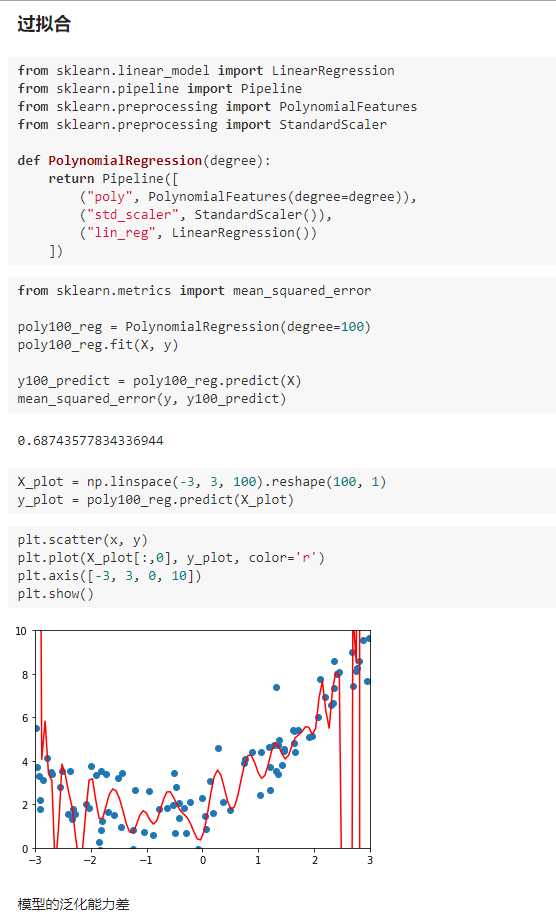
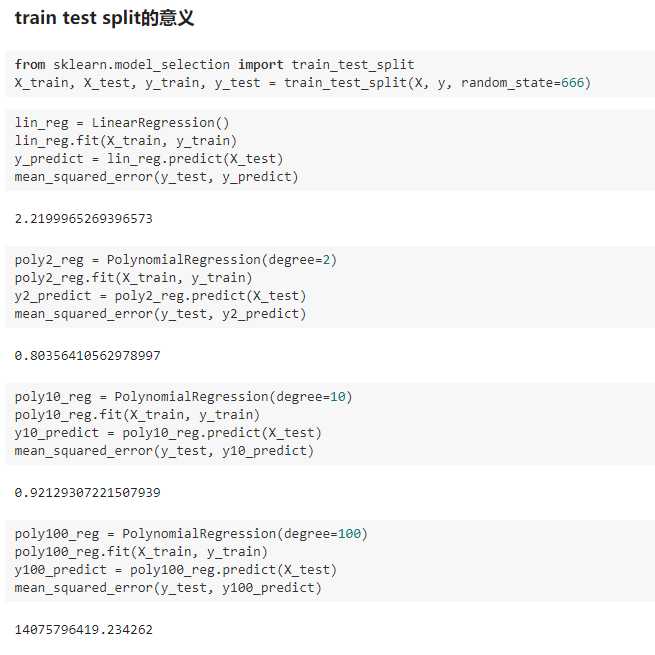
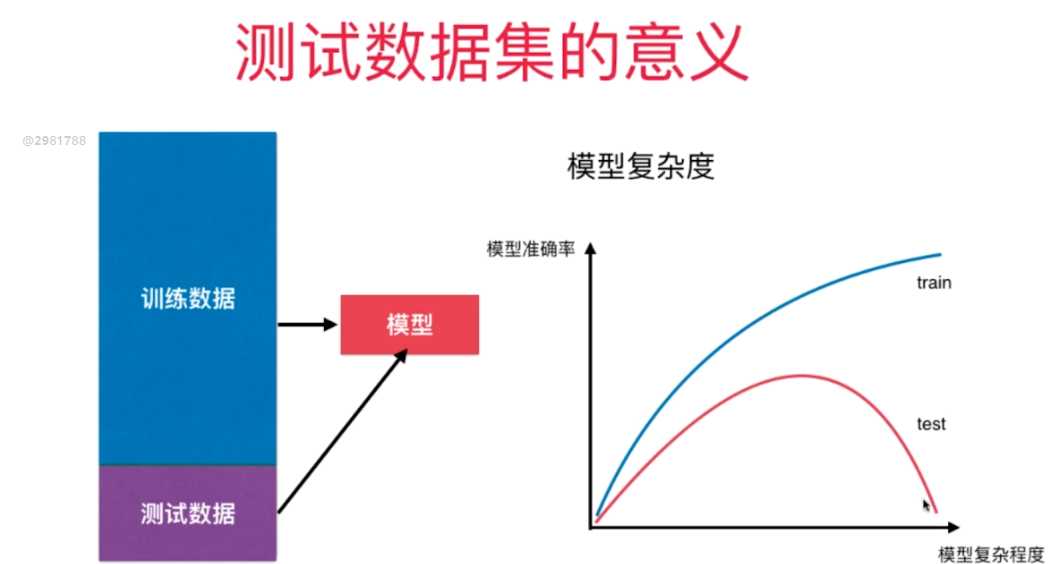
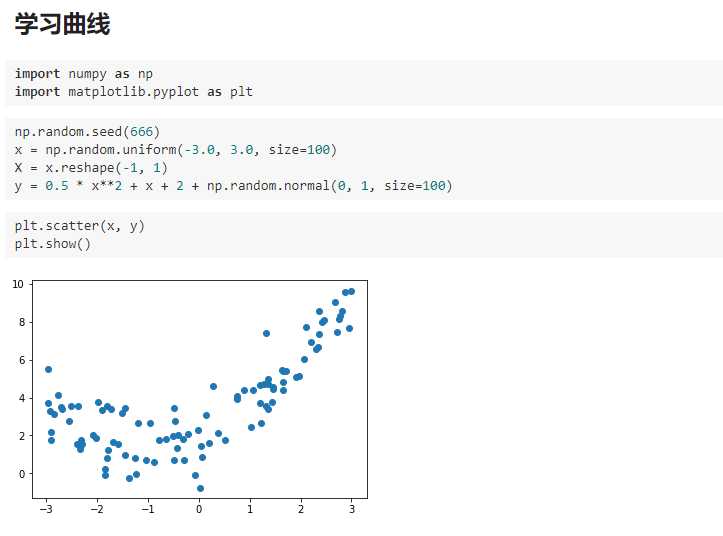
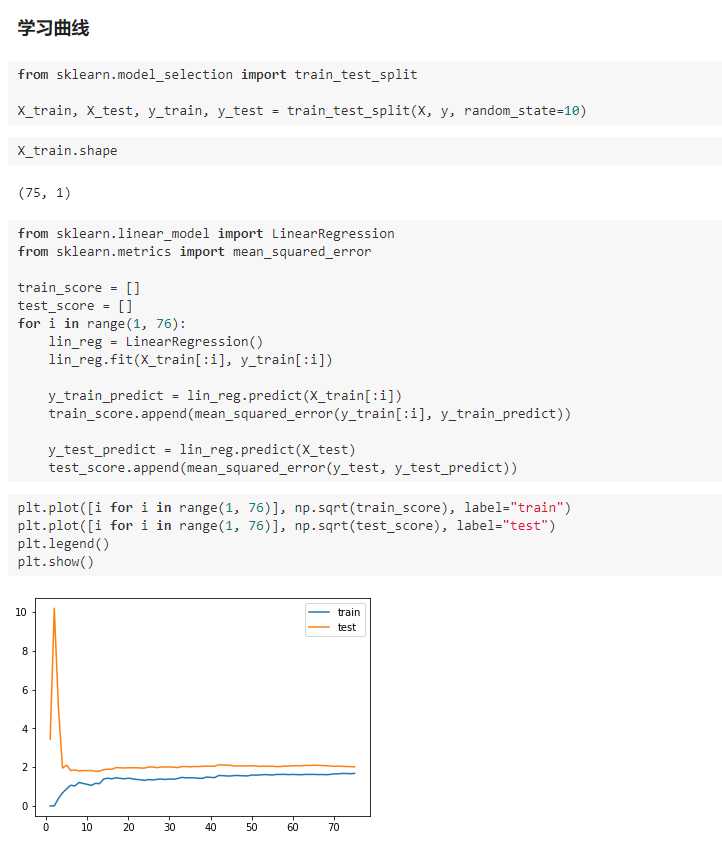
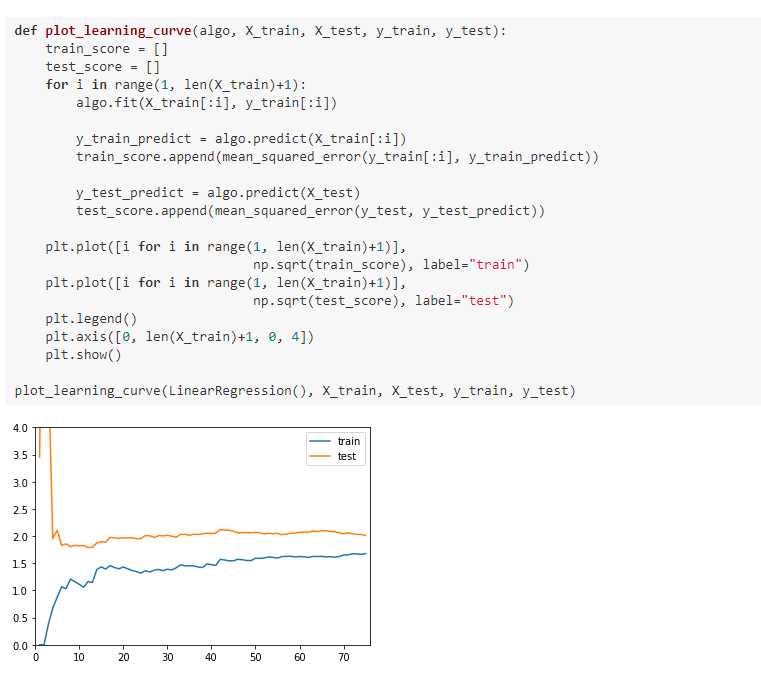
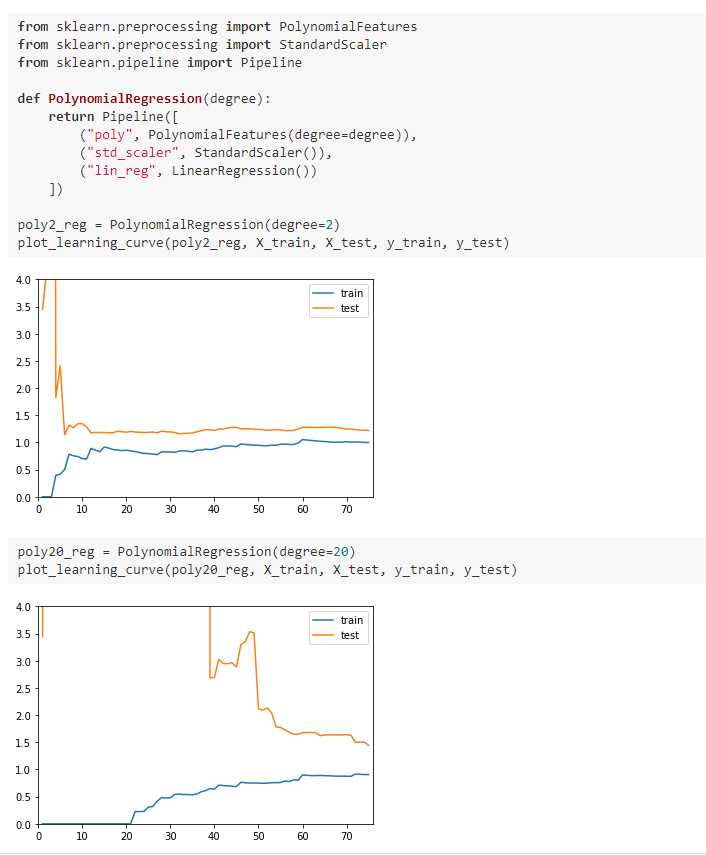
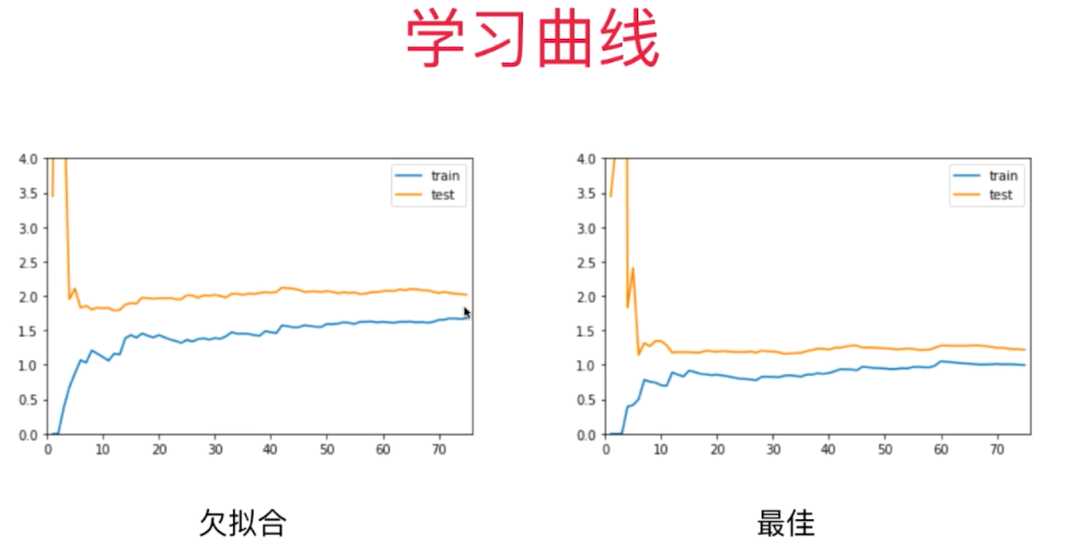
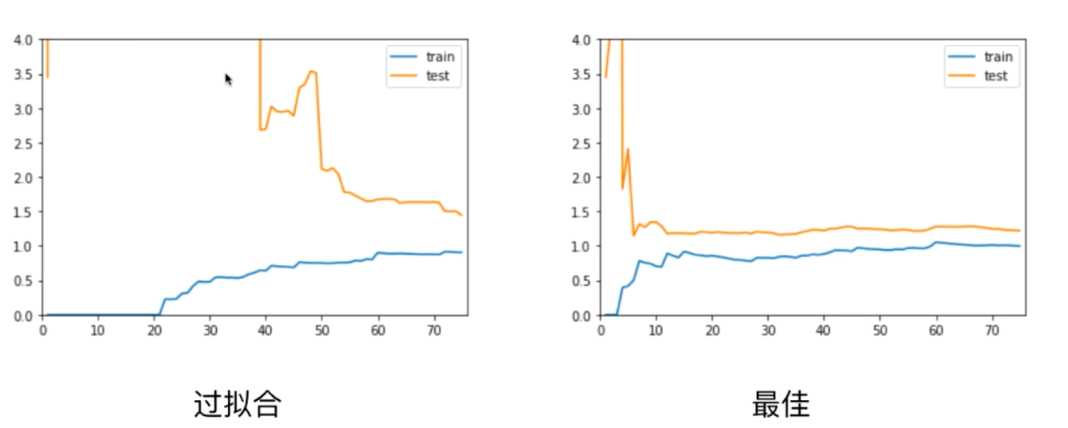
五、学习曲线