机器学习之路：python 多项式特征生成PolynomialFeatures 欠拟合与过拟合

Posted 2020-11-02 稀里糊涂林老冷

分享一下 线性回归中 欠拟合 和 过拟合 是怎么回事~
为了解决欠拟合的情 经常要提高线性的次数建立模型拟合曲线， 次数过高会导致过拟合，次数不够会欠拟合。
再建立高次函数时候，要利用多项式特征生成器 生成训练数据。
下面把整个流程展示一下
模拟了一个预测蛋糕价格的从欠拟合到过拟合的过程

git: https://github.com/linyi0604/MachineLearning

在做线性回归预测时候，为了提高模型的泛化能力，经常采用多次线性函数建立模型

f = k*x + b   一次函数
f = a*x^2 + b*x + w  二次函数
f = a*x^3 + b*x^2 + c*x + w  三次函数
。。。

泛化：
    对未训练过的数据样本进行预测。
    
欠拟合:
    由于对训练样本的拟合程度不够，导致模型的泛化能力不足。

过拟合：
    训练样本拟合非常好，并且学习到了不希望学习到的特征，导致模型的泛化能力不足。
    

在建立超过一次函数的线性回归模型之前，要对默认特征生成多项式特征再输入给模型

　　poly2 = PolynomialFeatures(degree=2)    # 2次多项式特征生成器
　　x_train_poly2 = poly2.fit_transform(x_train)

下面模拟 根据蛋糕的直径大小 预测蛋糕价格

 1 from sklearn.linear_model import LinearRegression
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 
 5 \'\'\'
 6 在做线性回归预测时候，
 7 为了提高模型的泛化能力，经常采用多次线性函数建立模型
 8 
 9 f = k*x + b   一次函数
10 f = a*x^2 + b*x + w  二次函数
11 f = a*x^3 + b*x^2 + c*x + w  三次函数
12 。。。
13 
14 泛化：
15     对未训练过的数据样本进行预测。
16     
17 欠拟合:
18     由于对训练样本的拟合程度不够，导致模型的泛化能力不足。
19 
20 过拟合：
21     训练样本拟合非常好，并且学习到了不希望学习到的特征，导致模型的泛化能力不足。
22     
23 
24 在建立超过一次函数的线性回归模型之前，要对默认特征生成多项式特征再输入给模型
25 
26 下面模拟 根据蛋糕的直径大小 预测蛋糕价格
27  
28 \'\'\'
29 
30 # 样本的训练数据，特征和目标值
31 x_train = [[6], [8], [10], [14], [18]]
32 y_train = [[7], [9], [13], [17.5], [18]]
33 
34 # 一次线性回归的学习与预测
35 # 线性回归模型 学习
36 regressor = LinearRegression()
37 regressor.fit(x_train, y_train)
38 # 画出一次线性回归的拟合曲线
39 xx = np.linspace(0, 25, 100)   # 0到16均匀采集100个点做x轴
40 xx = xx.reshape(xx.shape[0], 1)
41 yy = regressor.predict(xx)  # 计算每个点对应的y
42 plt.scatter(x_train, y_train)   # 画出训练数据的点
43 plt1, = plt.plot(xx, yy, label="degree=1")
44 plt.axis([0, 25, 0, 25])
45 plt.xlabel("Diameter")
46 plt.ylabel("Price")
47 plt.legend(handles=[plt1])
48 plt.show()

一次线性函数拟合曲线的结果，是欠拟合的情况：

 

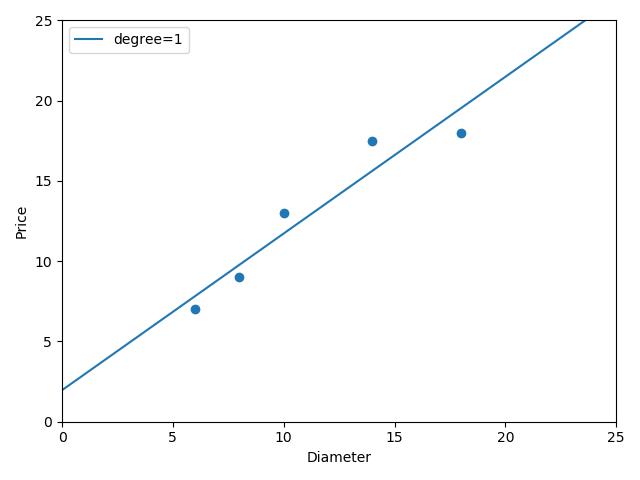
下面进行建立2次线性回归模型进行预测：

 1 # 2次线性回归进行预测
 2 poly2 = PolynomialFeatures(degree=2)    # 2次多项式特征生成器
 3 x_train_poly2 = poly2.fit_transform(x_train)
 4 # 建立模型预测
 5 regressor_poly2 = LinearRegression()
 6 regressor_poly2.fit(x_train_poly2, y_train)
 7 # 画出2次线性回归的图
 8 xx_poly2 = poly2.transform(xx)
 9 yy_poly2 = regressor_poly2.predict(xx_poly2)
10 plt.scatter(x_train, y_train)
11 plt1, = plt.plot(xx, yy, label="Degree1")
12 plt2, = plt.plot(xx, yy_poly2, label="Degree2")
13 plt.axis([0, 25, 0, 25])
14 plt.xlabel("Diameter")
15 plt.ylabel("Price")
16 plt.legend(handles=[plt1, plt2])
17 plt.show()
18 # 输出二次回归模型的预测样本评分
19 print("二次线性模型在训练数据上得分:", regressor_poly2.score(x_train_poly2, y_train))     # 0.9816421639597427

二次线性回归模型拟合的曲线：

拟合程度明显比1次线性拟合的要好

 

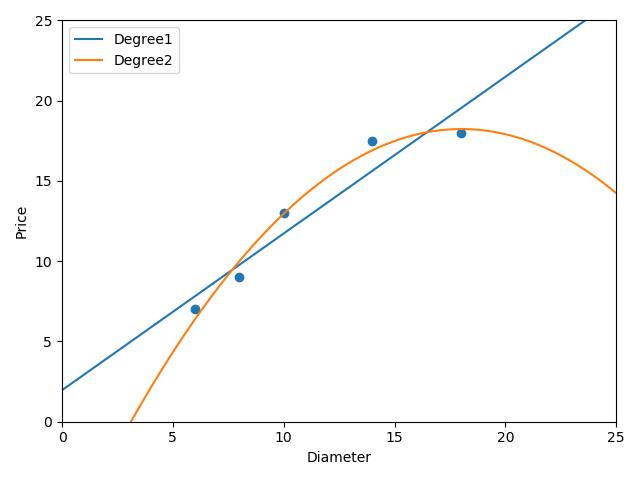
下面进行4次线性回归模型：

 1 # 进行四次线性回归模型拟合
 2 poly4 = PolynomialFeatures(degree=4)    # 4次多项式特征生成器
 3 x_train_poly4 = poly4.fit_transform(x_train)
 4 # 建立模型预测
 5 regressor_poly4 = LinearRegression()
 6 regressor_poly4.fit(x_train_poly4, y_train)
 7 # 画出2次线性回归的图
 8 xx_poly4 = poly4.transform(xx)
 9 yy_poly4 = regressor_poly4.predict(xx_poly4)
10 plt.scatter(x_train, y_train)
11 plt1, = plt.plot(xx, yy, label="Degree1")
12 plt2, = plt.plot(xx, yy_poly2, label="Degree2")
13 plt4, = plt.plot(xx, yy_poly4, label="Degree2")
14 plt.axis([0, 25, 0, 25])
15 plt.xlabel("Diameter")
16 plt.ylabel("Price")
17 plt.legend(handles=[plt1, plt2, plt4])
18 plt.show()
19 # 输出二次回归模型的预测样本评分
20 print("四次线性训练数据上得分:", regressor_poly4.score(x_train_poly4, y_train))     # 1.0

四次线性模型预测准确率为百分之百， 但是看一下拟合曲线，明显存在不合逻辑的预测曲线，

在样本点之外的情况，可能预测的非常不准确，这种情况为过拟合

 

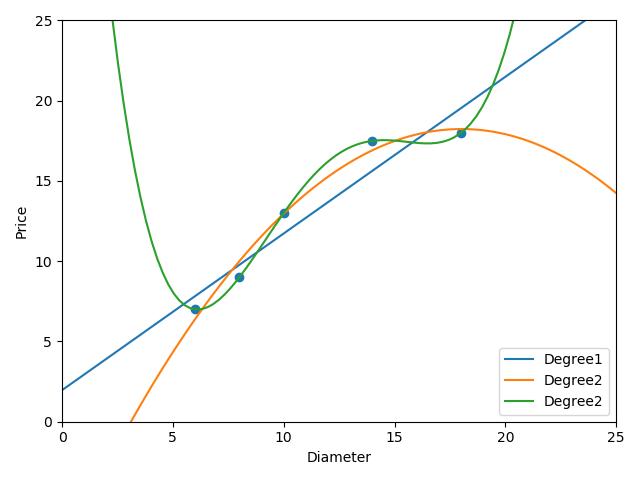
 之前我们一直在展示在训练集合上获得的模型评分，次数越高的模型，训练拟合越好。

下面查看一组测试数据进行预测的得分情况：

1 # 准备测试数据
2 x_test = [[6], [8], [11], [16]]
3 y_test = [[8], [12], [15], [18]]
4 print("一次线性模型在测试集合上得分:", regressor.score(x_test, y_test))   # 0.809726797707665
5 x_test_poly2 = poly2.transform(x_test)
6 print("二次线性模型在测试集合上得分:", regressor_poly2.score(x_test_poly2, y_test))   # 0.8675443656345054
7 x_test_poly4 = poly4.transform(x_test)
8 print("四次线性模型在测试集合上得分:", regressor_poly4.score(x_test_poly4, y_test))   # 0.8095880795746723

 

 会发现，二次模型在预测集合上表现最好，四次模型表现反而不好！

这就是由于对训练数据学习的太过分，学习到了不重要的东西，反而导致预测不准确。