树链剖分详解

Posted 2021-01-02 katoukatou

树链剖分详解

在学树链剖分之前，我们先得理解什么是树链剖分，以及它的应用

那么，什么是树链剖分呢(～￣▽￣)～

树链剖分就是将树分割成多条链，然后利用数据结构（线段树、树状数组等）来维护这些链。

看上去好像很好理解的样子！（实际上也的确是这样……），咳咳，那它到底有什么应用，先看一道水题：

e.g

给你一颗有根树，对区间进行两种操作：1.路径值修改（树上差分？）；2.查询路径和（LCA？）；

确实水到不行= =

不用莫队之类的操作，我们想要在低时间复杂度的情况下完成这两个操作，用求LCA的方法显然是不现实的，每次修改后都会花费(O（n）)的时间复杂度(dfs)更新(dis)值（求路径和原理：(Ans=dis[x]+dis[y]-2*lca(x,y))），当然，(dfs)序后线段树也是可行的，但是树链剖分可以解决的问题当然不是这种水题，这道题只是为了引路。

在正式开始学习树链剖分之前，我们先来看一些概念：

一些概念：

重儿子（吃的好的儿子）：儿子中子树中节点个数最大的儿子

轻儿子（吃的不好的儿子）：非重儿子的儿子

重边：连接父亲与重儿子的边

轻边：连接父亲与轻儿子的边

重链：重边构成的一条链

轻链：轻边构成的一条链

如图：

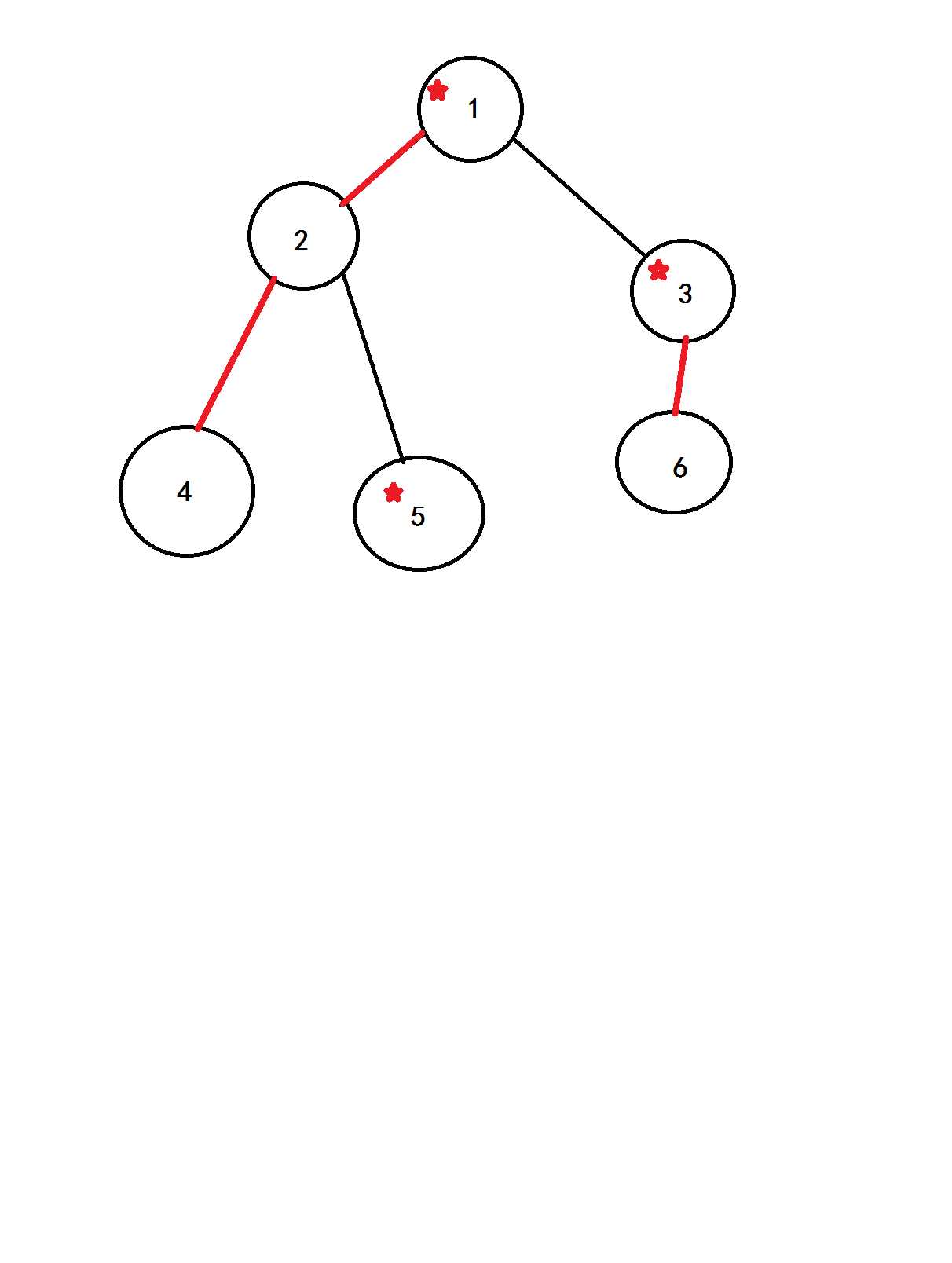
图中红色的边就是重边，而重边所连接的点就是重节点，而标上红色五角星的点就是后文的(top)节点，从图中我们也可以显然的发现，轻边上的叶子节点必然是(top)节点，我们之后也会用到

变量声明：

(dfn)：记录遍历后的(dfs)序

(pos)：记录(dfs)之后各节点在(dfn)中的编号（树上问题区间问题的思想）

(top)：重链的起点

(dep)：深度

(sz)：子节点个数

(son)：重儿子编号

---

那么，我们就要开始具体实现树链剖分啦！

首先，我们需要进行两次(dfs)：

1.记录深度维护重儿子父节点

2.连接重链，维护(top)节点，dfs序

为什么我们不在第一次ds中就维护所有的信息呢？因为：我们希望优先将重链连接起来，使其在(dfn)中成为连续的一个区间；当我们在选择重儿子时如果有多个儿子子节点个数相同，我们只需要随便选择一个就好。（此乃自然之理）

dfs1 code

void dfs1(ll x,ll pre)
{
    ll siz=G[x].size();
    sz[x]++;
    dep[x]=dep[pre]+1;
    fa[x]=pre;
    for(ll i=0,p=G[x][i]; i<siz; i++,p=G[x][i]) {
        if(p==pre) continue;
        dfs1(p,x);
        sz[x]+=sz[p];
        if(sz[p]>sz[son[x]]) son[x]=p;//更新重儿子
    }
}

dfs2 code

void dfs2(ll x,ll t,ll pre)
{
    top[x]=t;//继承父亲的top
    dfn[++tot]=x;
    pos[x]=tot;

    if(!son[x]) return;
    dfs2(son[x],t,x);//优先更新重儿子

    ll siz=G[x].size();
    for(int i=0,p=G[x][i]; i<siz; i++,p=G[x][i]) {
        if(p==pre||p==son[x]) continue;
        dfs2(p,p,x);//从之前的结论我们可以看出轻边上的叶子节点必然是top节点，即轻链底端必定是top节点
    }
}

那么我们如何解决查询操作呢：

ll solve(ll x,ll y)
{
    ll ans=0,fx,fy;
    for(fx=top[fa[x]],fy=fa[top[y]]; fx!=fy; fx=top[fa[x]]) {
        ans+=query(root,1,maxn,pos[fx],pos[fy],0);
        if(dep[fx]<dep[fy]) swap(fx,fy);//可以理解为从深度更深的往上快速跳转
    }
    if(pos[fx]>pos[fy]) swap(fx,fy);
    ans+=query(root,1,maxn,pos[fx],pos[fy],0);
    return ans;
}

从代码中我们也可以看出，这跟倍增的思想非常相似,只不过这里是使用top进行加速罢了

---

树链剖分的性质：

1.对于任意轻边((u,v))，(size(u)/2>size(v))

2.从根节点到任意节点经过的轻重链个数不会超过(log_2 N)

---

习题【SDOI2011 第1轮 DAY1】染色