『8.20 模拟赛』旋转的多边形

Posted 2020-12-31 fang-hao

题目链接戳着里！！

题目描述

 

 

解题思路

显然，多边形滚动的时候，指定的点一定是绕着某一个顶点旋转的，旋转的半径就是点到顶点的距离，角度就是顶点所在脚的外角。

如下图所示：

 

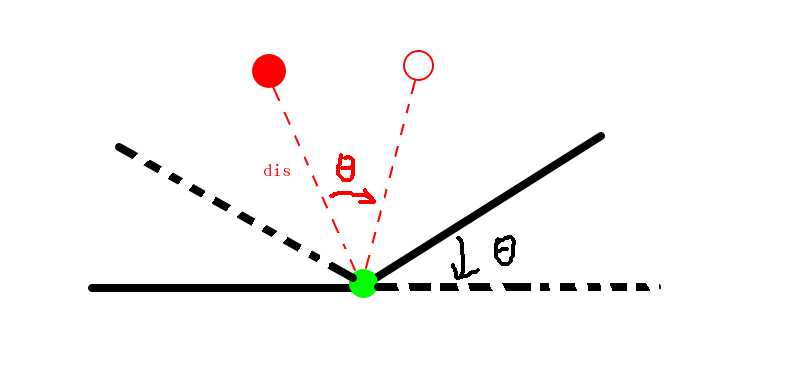
那么我们的问题就转化成了求dis和θ了。

dis很简单，只要勾股定理就好了。

那θ呢？也很简单喽，只要链接当前顶点的相邻的两个顶点，运用余弦定理求就好啦，注意一下角度值和弧度制就可以了。

（不会余弦定理的小伙伴戳这里==>  Wikipedia & 百度百科）

 

代码

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<algorithm>
 4 #include<cstring>
 5 #include<cmath>
 6 using namespace std;
 7 const double PI=acos(-1.0);
 8 struct nod{
 9     int x,y;
10     double dis,deg;
11 };
12 int n,xq,yq;
13 nod p[100];
14 double ans;
15 inline double gougu(int x1,int y1,int x2,int y2){
16     return (double)sqrt((double)((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)));
17 }
18 inline double yuxian(double dis1,double dis2,double dis3){
19     double cosc=(dis2*dis2+dis3*dis3-dis1*dis1)/(2*dis2*dis3);
20     cosc=acos(cosc);
21     cosc=cosc*180.0/PI;
22     return cosc;
23 }
24 inline void calc_dis(){
25     for(register int i=1;i<=n;i++){
26         p[i].dis=gougu(xq,yq,p[i].x,p[i].y);
27     }
28 }
29 inline void calc_deg(){
30     for(register int i=1;i<=n;i++){
31         int la=i-1,ne=i+1;
32         if(la==0)la=n;
33         if(ne==n+1)ne=1;
34         double dis1=gougu(p[la].x,p[la].y,p[ne].x,p[ne].y);
35         double dis2=gougu(p[la].x,p[la].y,p[i].x,p[i].y);
36         double dis3=gougu(p[i].x,p[i].y,p[ne].x,p[ne].y);
37         p[i].deg=yuxian(dis1,dis2,dis3);
38     }
39 }
40 inline void calc(){
41     for(register int i=1;i<=n;i++){
42         ans+=2.0*PI*p[i].dis*((180.0-p[i].deg)/360.0);
43     }
44 }
45 int main(){
46     scanf("%d",&n);
47     for(register int i=1;i<=n;i++){
48         scanf("%d%d",&p[i].x,&p[i].y);
49     }
50     scanf("%d%d",&xq,&yq);
51     calc_dis();
52     calc_deg();
53     calc();
54     printf("%.3f
",ans);
55 }