hdu GuGuFishtion 6390 数论 欧拉函数
Posted dcd112358
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了hdu GuGuFishtion 6390 数论 欧拉函数相关的知识,希望对你有一定的参考价值。
题目:http://acm.hdu.edu.cn/showproblem.php?pid=6390
直接开始证明:
我们设![]() …………………………………….....…...............……………...(1)
…………………………………….....…...............……………...(1)
则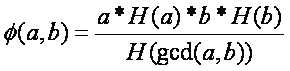 …................................….…(2)
…................................….…(2)
为什么是这样呢,因为我们知道
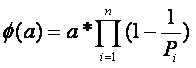
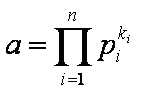
同理得到b的分解和的分解
我们会发现,虽然a和b的分解里可以有相等的部分,但是在里的也就是我们假设为的部分是不会有重复的,那么要由*得出也就是要去除重复部分,的重复部分就是a的和b的的重复部分;那么因为都是乘法,相同的部分就是最大公约数(因为每个都是素数也就是如果a和b的分解没有相同的数那么gcd(, )是不会大于1的);
由此我们开始继续对(2)的后续推论。
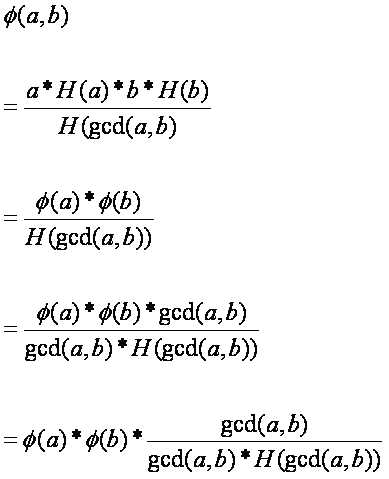
我先设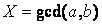 ,那么
,那么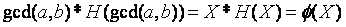
也就是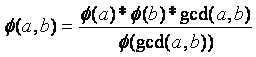
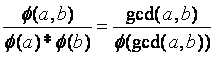 (看了很多博客,就给了个易得,虽然说确实很简单但是对于我这个菜鸡就不友好了)
(看了很多博客,就给了个易得,虽然说确实很简单但是对于我这个菜鸡就不友好了)
这一部分的证明是看了这个大佬的博客的:http://www.cnblogs.com/H-Riven/p/9494391.html
(再提供给同样是数论萌新的人一篇文库【有需要的话】:https://wenku.baidu.com/view/542961fdba0d4a7302763ad5.html)
设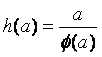
设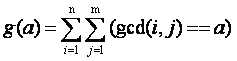 (即在
(即在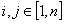 的情况下
的情况下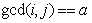 的数量)
的数量)
那么我们实际上就是要求: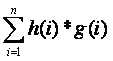 ,对于
,对于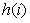 我们可以预处理得到。但是
我们可以预处理得到。但是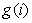 就没那么容易得到了;
就没那么容易得到了;
现在题目就变成求对于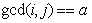 ,在
,在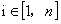 、
、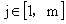 的情况下有多少种方案;
的情况下有多少种方案;
这里我设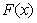 为
为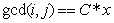 的数量 (C*x表示x的倍数);即可以和HDU1695一样得到
的数量 (C*x表示x的倍数);即可以和HDU1695一样得到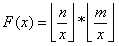 的结论
的结论
设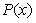 为
为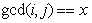 的数量
的数量
那么:
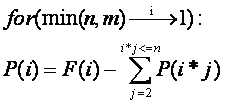
倒过来求的原因是因为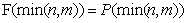 ,也就是我们可以知道最后一位的准确值,那么反过来就可以推到每个位置准确值了;
,也就是我们可以知道最后一位的准确值,那么反过来就可以推到每个位置准确值了;
那么答案就已经出来了;又因为要求的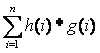 ,对于每个
,对于每个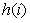 ,是含有有除法的,所以这里要用除法逆元,因为每次的mod都是不同的,所以说每次都要得到逆元,因为
,是含有有除法的,所以这里要用除法逆元,因为每次的mod都是不同的,所以说每次都要得到逆元,因为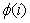 一定会小于min(n,m);所以说每次打从1到 min(n,m)的表比单个值的计算快;
一定会小于min(n,m);所以说每次打从1到 min(n,m)的表比单个值的计算快;
以下是代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N=2e6+7; 5 ll euler[N], inv[N]={1, 1}, F[N], P[N], n, m, mod, mins; 6 void Euler(){///打欧拉表 7 register int i, j; 8 for(i=0; i<N; ++i){ euler[i]=i; } 9 for(i=2; i<N; ++i){ 10 if(euler[i]==i){ 11 for(j=i; j<N; j+=i) 12 euler[j]=euler[j]-euler[j]/i; 13 } 14 } 15 } 16 void Inv(){///打表求逆元 17 for(register int i=2; i<=mins; ++i){ 18 inv[i]=(ll)(mod-mod/i)*inv[mod%i]%mod; 19 } 20 } 21 int main( ){ 22 Euler(); 23 int T; 24 register ll ans; 25 register int i, j; 26 scanf("%d", &T); 27 while(T--){ 28 scanf("%I64d%I64d%I64d", &n, &m, &mod); 29 mins=min(n, m); 30 Inv(); 31 for(i=1; i<=mins; ++i){ 32 F[i]=(n/i)*(m/i)%mod; 33 } 34 for(i=mins; i>=1; --i){ 35 P[i]=F[i]; 36 for(j=2; j*i<=mins; ++j){ 37 P[i]-=P[i*j]; 38 if(P[i]<0){ 39 P[i]+=mod; 40 } 41 } 42 } 43 ans=0; 44 for(i=1; i<=mins; ++i){ 45 ans=(ans+(i*inv[euler[i]]%mod)*P[i]%mod)%mod; 46 } 47 printf("%I64d ", ans); 48 } 49 }
以上是关于hdu GuGuFishtion 6390 数论 欧拉函数的主要内容,如果未能解决你的问题,请参考以下文章
E - GuGuFishtion HDU - 6390(欧拉函数 / 莫比乌斯反演)
hdu 6390 欧拉函数+容斥(莫比乌斯函数) GuGuFishtion
HDU 6390 GuGuFishtion(莫比乌斯反演 + 欧拉函数性质 + 积性函数)题解
