2018/8/15 qbxt 测试

Posted 2020-12-30 v-vip

　　　　　　2018/8/15 qbxt 测试

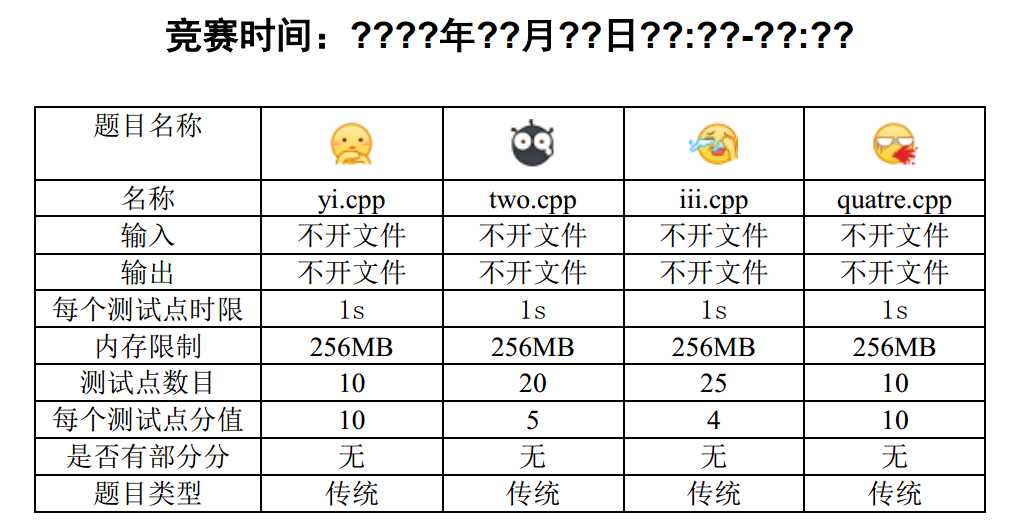
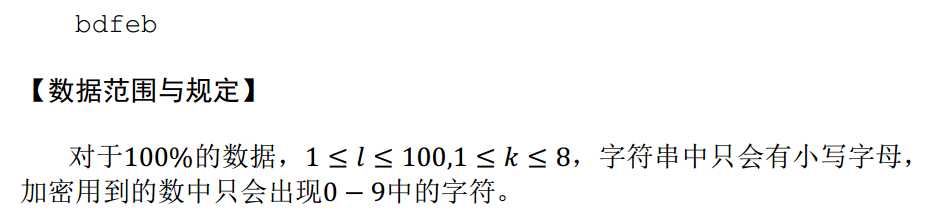
期望得分：100；实际得分：50   不知道为什么写挂了，明明是个水题 T^T

思路：模拟

注意：如果用 char 类型存储的话，如果有‘z‘ + 9 会爆char  但是我明明用的 string 啊

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int n, m;
int len;
string s, ss;

int main() {
    scanf("%d%d", &n, &m);
    cin >> s >> ss;
    len = s.length();
    for(int i = 0; i < len; i++) {
        s[i] += ss[i%m] - ‘0‘;
        if(s[i] > ‘z‘) s[i] = s[i] - ‘z‘ + ‘a‘ - 1;
    }
    cout << s << ‘
‘;
    return 0;
}

考场代码

#include <cstdio>

#define next(i) ((i) == K-1 ? 0 : (i) + 1)

int main() {
    int L, K;
    scanf("%d%d", &L, &K);
    char * s1 = new char[L + 2];
    char * s2 = new char[K + 2];
    
    scanf("%s%s", s1, s2);
    
    int j = 0;
    for (int i=0; i<L; i++, j = (j==K-1 ? 0 : j+1))
        s1[i] = ((s1[i] - ‘a‘) + (s2[j] - ‘0‘)) % 26 + ‘a‘;
    
    puts(s1);
    return 0;    
}

std

 

 

期望得分：100；实际得分：100

思路：将因为是完全平方数，所以这个数的因子在1~n中一定是出现了偶数次，道理显然，否则一定不会出现这样一个数。因此我们可以对于N分解质因数，用线性筛O(N)求出1~n的素数。求出素数后用N除以每个素数，开一个数组记录一下出现的次数，对于除出来的商，我们在判断一下能否在继续除以当前的素数，能继续除就继续加，道理显然。 
因此，如果数组中记录的数为奇数，就-1，这样就能保证以上偶数次的要求。

#include<iostream>
#include<cstdlib>
#include<cstdio>
#define LL long long
using namespace std;
const int maxn = 5000005;
const LL mod = 100000007;
bool not_prime[maxn];
int cnt;
LL n, ans=1;
LL prime[maxn];
LL num[maxn];

LL ksm(LL a, LL b) {
    if(b == 0) return 1ll;
    if(b == 1) return a%mod;
    LL tmp = ksm(a, b/2)%mod;
    if(b%2 == 0)
        return ((tmp%mod)*(tmp%mod))%mod;
    else
        return ((((tmp%mod)*tmp)%mod)*(a%mod))%mod;
}
int main() {
    scanf("%lld", &n);
    not_prime[1] = true;
    for(LL i = 2; i <= n; i++) {
        if(!not_prime[i])
            prime[++cnt] = i;
        for(int j = 1; j <= cnt; j++) {
            if(prime[j]*i>n) break;
            not_prime[prime[j]*i] = true;
            if(i%prime[j] == 0) break;
        }
    }
    for(int i = 1; i <= cnt; i++) {
        LL aa = n;
        while(aa != 0) {
            num[i] += aa/prime[i];
            aa /= prime[i];
        }
    }
    for(int i = 1; i <= cnt; i++) {
        if(num[i]%2 == 0)
            ans = (ans*ksm(prime[i], num[i]))%mod;
        else
            ans = (ans*ksm(prime[i], num[i]-1))%mod;
    }
    printf("%lld", ans);
    return 0;
}

考场代码

 

期望。。。不要爆零   实际。。。8分  qwq

思路：一看就是图论题，然后手动模拟了一下样例1，开始码代码。。发现后两个样例过不了我居然还以为样例错了，还去问老师。。傻的一批

正解：跑两边Floyd，第一次不考虑换马的情况求出最短路，第二次则要考虑换马 f[i][j] = min(f[i][k]+f[k][j]);

#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#define M 10005
#define MAXN 0x3f3f3f
using namespace std;
queue<int> q;
int s, f;
int n, m, tot;
int e[M], v[M];
double dis[M], cap[M];
int to[M], net[M], head[M], vis[M];

void add(int u, int v, double w) {
    to[++tot] = v; net[tot] = head[u]; head[u] = tot; cap[tot] = w;
}
void spfa(int x) {
    for(int i = 1; i <= n; i++)
        dis[i] = 1.0*MAXN, vis[i] = 0;
    dis[x] = 0; vis[x] = 1; q.push(x);
    while(!q.empty()) {
        int y = q.front(); q.pop(); vis[y] = 0;
        for(int i = head[y]; i; i = net[i]) {
            int t = to[i];
            if(dis[t] > dis[y] + cap[i]) {
                dis[t] = dis[y] + cap[i];
                if(!vis[t]) vis[t] = 1, q.push(t);
            }
        }
    }
//    for(int i = 1; i <= n; i++) printf("%lf
", dis[i]);
}

int main() {
    
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
        scanf("%d%d", &e[i], &v[i]);
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++) {
            int a;
            scanf("%d", &a);
            if(a == -1) continue;
            else if(e[i] < a) continue;
            else {
                double tmp = 1.0 * a / v[i];
                add(i, j, tmp);
            }
        }
    for(int i = 1; i <= m; i++) {
        scanf("%d%d", &s, &f);
        spfa(s);
        printf("%.6lf
", dis[f]);
    }
    return 0;
}

考场代码

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>

using namespace std;

const int maxn=110;

int n,q,e[maxn],s[maxn];

double dis[maxn][maxn],dist[maxn][maxn];

int main()
{
    int T=1;
    for (int t=1;t<=T;t++)
    {
        scanf("%d%d",&n,&q);
        for (int a=1;a<=n;a++)
            scanf("%d%d",&e[a],&s[a]);
        for (int a=1;a<=n;a++)
            for (int b=1;b<=n;b++)
            {
                scanf("%lf",&dis[a][b]);
                if (dis[a][b]<0) dis[a][b]=1e+20;
                if (a==b) dis[a][b]=0;
            }
        for (int a=1;a<=n;a++)
            for (int b=1;b<=n;b++)
                for (int c=1;c<=n;c++)
                    dis[b][c]=min(dis[b][c],dis[b][a]+dis[a][c]);
        for (int a=1;a<=n;a++)
            for (int b=1;b<=n;b++)
                dist[a][b]=1e+20;
        for (int a=1;a<=n;a++)
            dist[a][a]=0;
        for (int a=1;a<=n;a++)
            for (int b=1;b<=n;b++)
                if (dis[a][b]<=e[a]) dist[a][b]=dis[a][b]/s[a];
        for (int a=1;a<=n;a++)
            for (int b=1;b<=n;b++)
                for (int c=1;c<=n;c++)
                    dist[b][c]=min(dist[b][c],dist[b][a]+dist[a][c]);
        //printf("Case #%d:",t);
        for (int a=1;a<=q;a++)
        {
            int s,e;
            scanf("%d%d",&s,&e);
            printf("%.6lf
",dist[s][e]);
        }
    }

    return 0;
}

std

 

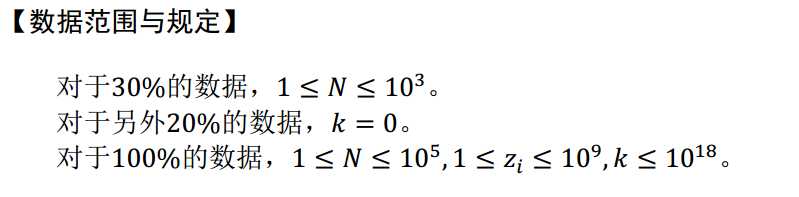
期望。。。不要爆零  实际。。骗分得到了10分   因为测试点数量比上一个少 qwq

 思路：类似于滑动窗口，然后通过树状数组求解

树状数组似撒？能吃吗？qwq

骗分代码我就不展示了  捂脸

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>

using namespace std;

#ifdef unix
#define LL "%lld"
#else
#define LL "%I64d"
#endif

#define lb(x) ((x)&(-(x)))

const int maxn=100010;

int n,z[maxn],y[maxn],x[maxn];

long long k;

bool cmp(int a,int b) {
    return z[a]<z[b];
}

void insert(int *z,int p,int d) {
    for (; p<=n; p+=lb(p))
        z[p]+=d;
}

int query(int *z,int p) {
    int ans=0;
    for (; p; p-=lb(p))
        ans+=z[p];
    return ans;
}

int main() {
    scanf("%d" LL,&n,&k);
    for (int a=1; a<=n; a++)
        scanf("%d",&z[a]),y[a]=a;
    sort(y+1,y+n+1,cmp);
    x[y[1]]=1;
    for (int a=2; a<=n; a++)
        if (z[y[a]]==z[y[a-1]]) x[y[a]]=x[y[a-1]];
        else x[y[a]]=x[y[a-1]]+1;
    for (int a=1; a<=n; a++)
        z[a]=x[a];
    memset(x,0,sizeof(x));
    memset(y,0,sizeof(y));
    long long nowans=0;
    int p=n;
    while (p>=1) {
        nowans+=query(y,z[p]-1);
        insert(y,z[p],1);
        p--;
    }
    p++;
    long long ans=0;
    for (int a=1; a<=n; a++) {
        if (p==a) {
            nowans-=a-1-query(x,z[p])+query(y,z[p]-1);
            insert(y,z[p],-1);
            p++;
        }
        nowans+=a-1-query(x,z[a])+query(y,z[a]-1);
        insert(x,z[a],1);
        while (nowans>k && p<=n) {
            nowans-=a-query(x,z[p])+query(y,z[p]-1);
            insert(y,z[p],-1);
            p++;
        }
        if (nowans<=k) ans+=n-p+1;
    }
    printf(LL "
",ans);

    return 0;
}

std