点分治详解

Posted 2020-12-29 ender-zzm

点分治详解

一.概念

? 是处理树上路径的一个极好的方法。如果你需要大规模的处理一些树上路径的问题时，点分治是一个不错的选择。

二.具体思路

? 大多数同学的暴力做法都是对于每一个点对（u，v） 进行dfs来求解。但其实利用分治这一种算法，可以大大减少搜索的时间复杂度。

? 对于一个序列上的区间和等操作，我们可以使用分治来将原问题分解成几个子问题来求解，之后在一一合并答案。而在树上我们也是可以进行这一种操作的。可是树上的每一个子树的节点数是不确定的，不能单单的取中点（你告诉我怎么取），或直接取一号子树。（分治的点的错误选择会导致时间复杂度十分不稳定）。

? 如下图所示，如果你取了第一个点的话，那么时间复杂度会变$O(n)$,但如果我们取的点是3的话，那么时间复杂度就会是$O(logn)$

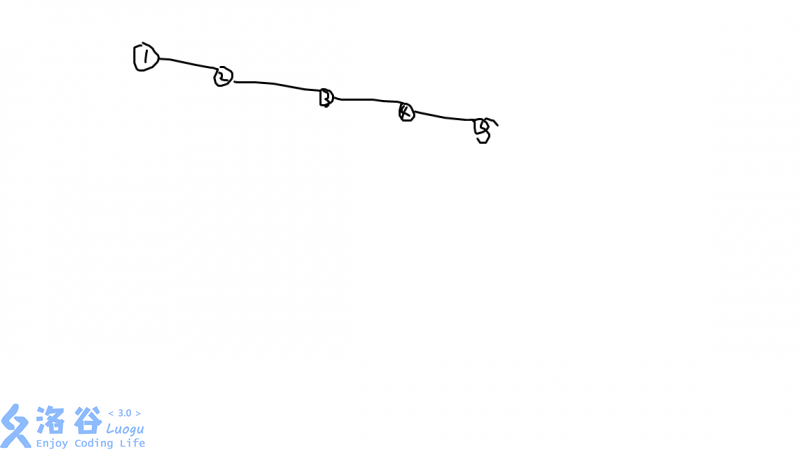
? 所以，我们要引入一个概念 —— 树的重心

? 定义：找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后，生成的多棵树尽可能平衡

? 由定义可知，当我们选择树的重心为分支点时，是最优的（我有个绝妙的证明只是这里写不下）

? 好了，求出了树的重心之后我们就可以来分治了！！

? 先现给出求重心的代码，便于读者依次理解

void find(int x,int fa)
{
 size[x] = 1; mx[x] = 0;
 for (int i = head[x]; i ; i = edges[i].net)
 {
     edge v = edges[i];
     if(v.to == fa||vis[v.to] ) continue;//vis是之后分治是要用到的
     find(v.to,x);
     size[x] += size[v.to];
     chkmax(mx[x],size[v.to]);
 }
 chkmax(mx[x],S-size[x]);//S为树的大小，记住x的上面要算入的
 if(mx[x] < mx[root])
 {
     root = x;
 }
}

? 现在开始我们点分治中最重要的部分了 —— 分治

? 分治不太好讲，我们从代码开始分析

void Divid(int x)
{
   ans+=solve(x,0);
   vis[x] = 1;
   for (int i = head[x];i;i = edges[i].net)
   {
       edge v = edges[i];
       if(vis[v.to]) continue;
       ans-=solve(v.to,edges[i].cost);
       S = size[v.to]; root = 0;
       find(v.to,x);
       Divid(root);
   }
}

1. ans += solve(x,0); 这一句的作用是将答案加上经过x的路径答案。 而这一个0是为了解决掉一些，有重复计算的结果；（看不懂先假装没有这个0）
2. ans -= solve（v.to,edges[i].cost); 这一句是将在既经过x这个点，又经过v.to这一个点的路径来去重。因为像这种路径会在solve（x,0)和solve(v.to,0)中都计算一次。而题目是要求路径的长度，所以在容斥时要初始化这条边的长度。所以，现在有没有理解这个0和edges[i].cost?
3. S = size[v.to]; 现在我们要分治v.to的这一颗子树，So，又将求重心的树的大小改为size[v.to];

到此为止，点分治就在这里讲完了，solve函数是看题目的，有能力的同学可以切一切这两道题（这两道题会在下面进行讲解）。luogu模板题 和聪聪可可.

三.例题分析

? 1.luogu模板题

? 题面在上面。

? 因为题目是要求路径长为k的路径条数，所以solve函数返回的是过x节点的长度为k的路径。

而这路径长度是可以用$O(n)$的方法求出

// luogu-judger-enable-o2
#include<bits/stdc++.h>
template <class T>
inline void read(T &a)
{
   T s = 0, w = 1;
   char c = getchar();
   while(c < ‘0‘ || c > ‘9‘)
   {
       if(c == ‘-‘) w = -1;
       c = getchar();
   }
   while(c >= ‘0‘ && c <= ‘9‘)
   {
       s = (s << 1) + (s << 3) + (c ^ 48);
       c = getchar();
   }
   a = s*w;
}
template<class T> void chkmax(T &a, T b) {a > b ? (a = a) : (a = b);}
template<class T> void chkmin(T &a, T b) {a > b ? (a = b) : (a = a);}
template<class T> T min(T a, T b) {return a > b ? b : a;}
template<class T> T max(T a, T b) {return a < b ? b : a;}

int n,m;
int S;
int size[10101];
struct edge{
   int from,to,cost,net;
   edge(int f = 0, int t = 0, int cost = 0, int nex = 0)
   {
       from = f;
       to = t;
       this->cost = cost;
       net = nex;
   }
}edges[1010101];
int tot,head[101001],mx[101011],minn =0x3f3f3f3f,root;
int vis[1010110];
void add(int x, int y, int z)
{
   edges[++tot] = edge(x,y,z,head[x]);
   head[x] = tot;
}
void find(int x,int fa)
{
   size[x] = 1;mx[x] = 0;
   for (int i = head[x];i; i =edges[i].net)
   {
       edge v = edges[i];
       if(v.to == fa || vis[v.to]) continue;
       find(v.to,x);
       size[x] += size[v.to];
       chkmax(mx[x],size[v.to]);
   }
   chkmax(mx[x], S - size[x]);
   if(mx[x] < mx[root])
   {
       root = x;
   }
  
}
int que[1010110],ans[102210101];
int dis[1010101],hhd,a[10101101];
void get_dis(int x, int len, int fa)
{
   dis[++hhd] = a[x];
   for (int i = head[x]; i; i = edges[i].net)
   {
       edge v = edges[i];
       if(vis[v.to]||v.to == fa) continue;
       a[v.to] = len + edges[i].cost;
       get_dis(v.to,len + edges[i].cost,x);
   }
}
void solve(int s, int len, int w)
{
   hhd = 0;
   a[s] = len;
   get_dis(s,len,0);
       for (int i1 = 1; i1 <= hhd; i1++)
           for (int i2 = 1; i2 <= hhd; i2++)
           {
               if(i1 != i2)
               {
                   ans[dis[i1] + dis[i2]] += w;
               }
           }
}
void Divide(int x)
{   
   solve(x,0,1);
   vis[x] = 1;
   for (int i = head[x]; i; i = edges[i].net)
   {
       edge v = edges[i];
       if(vis[v.to]) continue;
       solve(v.to,edges[i].cost,-1);
       S = size[x];root = 0; mx[0] = n;
       find(v.to,x);
       Divide(root);
   }
}
int main()
{
   read(n); read(m);
   for (int i = 1; i < n; i++)
   {
       int x,y,z;
       read(x); read(y); read(z);
       add(x,y,z);
       add(y,x,z);
   }
   S = n;mx[0] = n;root = 0;
// minn = 0x3f3f3f3f;
   find(1,0);    
  // printf("%d
",mx[root]);
   Devede(root);
   for (int i = 1; i <= m; i++)
   {
       int k;
       read(k);
       printf("%s
",(ans[k]) ? "AYE" : "NAY");
       //printf("%d
",ans[k]);
   }
   return 0;
}

? 2.聪聪可可

? 这道题是来求长度被3整除的路径条数，但处理方法跟上一条不太一样。

我们可以设p[0],p[1],p[2]为除3余数为0,1,2的 路径条数。显然答案为$p_0^2$ + $p_1 * p_2 * 2$

// luogu-judger-enable-o2
// luogu-judger-enable-o2
// luogu-judger-enable-o2
#include<bits/stdc++.h>
int gcd(int x, int y)
{
    if(y == 0) return x;
    return gcd(y,x%y);
}
template<class T>
inline void read(T &a)
{
    T s = 0,w = 1;
    char c = getchar();
    while(c < ‘0‘ || c > ‘9‘)
    {
        if(c == ‘-‘) w = -1;
        c = getchar();
    }
    while(c >= ‘0‘ && c <= ‘9‘)
    {
        s = (s << 1) + (s << 3) + (c ^ 48);
        c = getchar();
    }
    a = s*w;
}
template<class T> void chkmax(T &a, T b){a > b? (a = a) : (a = b);}
template<class T> void chkmin(T &a, T b){a > b ? (a = b):(a = a);}
int n;
struct edge{
    int from, to,cost,net;
    edge(int f = 0, int t = 0, int c = 0, int n = 0)
    {
        from = f;
        to = t;
        cost = c;
        net = n;
    }
}edges[2010101];
static int head[20010],tot;
void add(int x, int y, int z)
{
    edges[++tot] = edge(x,y,z,head[x]);
    head[x] = tot;
}
static int vis[20010],size[20010],mx[20010],root,S; 
void find(int x,int fa)
{
    size[x] = 1; mx[x] = 0;
    for (int i = head[x]; i ; i = edges[i].net)
    {
        edge v = edges[i];
        if(v.to == fa||vis[v.to] ) continue;
        find(v.to,x);
        size[x] += size[v.to];
        chkmax(mx[x],size[v.to]);
    }
    chkmax(mx[x],S-size[x]);
    if(mx[x] < mx[root])
    {
        root = x;
    }
}
int dis[20010],a[20010],cnt;
int ans,p[3];
void get_dis(int x, int fa)
{
  //  dis[++cnt] = a[x];
    p[a[x]%3]++;
    for (int i = head[x] ;i; i = edges[i].net)
    {
        edge v = edges[i];
        if(v.to == fa ||vis[v.to] ) continue;
        a[v.to] = a[x]+v.cost;
        get_dis(v.to,x);
    }
}
int  solve(int x, int len)
{
    a[x] = len;
    //cnt = 0;
    p[0] = p[1] = p[2] = 0;
    get_dis(x,0);
    return (p[0]*p[0] + 2 * p[1] * p[2]);
}
void Deved(int x)
{
    ans+=solve(x,0);
    vis[x] = 1;
    for (int i = head[x];i;i = edges[i].net)
    {
        edge v = edges[i];
        if(vis[v.to]) continue;
        ans-=solve(v.to,edges[i].cost);
        S = size[v.to]; root = 0;
        find(v.to,x);
        Deved(root);
    }
}
int main()
{
    //freopen("xx.in","r",stdin);
    //freopen("xx.out","w",stdout);
    read(n);
    for (register int i = 1; i < n; i++)
    {
        int x,y,z;
        read(x); read(y); read(z);
        z%=3;
        add(x,y,z);
        add(y,x,z);
    }
    S = n;root = 0; mx[0] = n+1; 
    find(1,0);
    Deved(root);
    int pp = gcd(ans,n*n);
    printf("%lld/%lld
",ans/pp,n*n/pp);
   // std::cerr<<std::clock()<<std::endl;
    return 0;
}