机器学习实战之一---简单讲解决策树
Posted dicksonjyl
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习实战之一---简单讲解决策树相关的知识,希望对你有一定的参考价值。
机器学习实战之一---简单讲解决策树
前言:本文基于《机器学习实战》一书,采用python语言,对于机器学习当中的常用算法进行说明。
一、 综述
定义:首先来对决策树进行一个定义,决策树是一棵通过事物的特征来进行判断分支后得到该事物所需要的预测的属性的树。
流程:提取特征à计算信息增益à构建决策树à使用决策树进行预测
关键:树的构造,通过信息增益(熵)得到分支点和分支的方式。
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配问题(过拟合)。
适用数据类型:数值型和标称型。
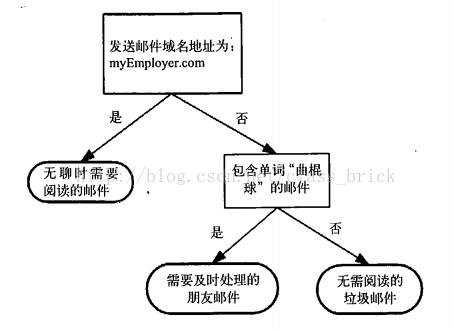
以下是一棵决策树的简单例子,通过邮件的一些特征,来判断一个邮件的类型。
图1
二、 特征提取
此处的特征指的就是用以构造决策树的实体集的特征,此处给出一个用以构造决策树的例子。
|
cheep |
buy |
|
|
1 |
1 |
Yes |
|
1 |
1 |
Yes |
|
1 |
0 |
No |
|
0 |
1 |
No |
|
0 |
1 |
No |
表1
简单的对表1中的数据进行一个说明,表1表征了小明在购物时基于一个商品便宜(cheep)与否(1/0)以及质量(quality)好坏(1/0)做出的购买选择。
此处的特征可以用一个python函数来创建:
def createDataSet(): dataSet = [ #数据集对应表格 [1, 1, ‘yes‘], [1, 1, ‘yes‘], [1, 0, ‘no‘], [0, 1, ‘no‘], [0, 1, ‘no‘] ] labels = [‘cheep‘, ‘quality‘]#标签对应价格与质量 return dataSet, labels
三、 计算信息增益
1、信息增益的介绍
信息增益是决策树在构造过程中节点的位置即特征判断的先后顺序的主要依据,计算信息增益可以帮助我们在多个特征当中选取选取对获得预测值帮助最大的特征,然后以此来对树当中的节点顺序进行划分。
结合二当中给出的例子,一件商品有价格便宜与否以及质量好坏两个特征,我们需要做的是把这两个特征作为节点放到树中,然后通过便不便宜以及质量好不好来对是否购买这件商品做出决策。而这里就存在一个问题,先判断价格还是先判断质量,这里就可以通过信息增益来做出一个决断。在每一次构造树的时候进行一次信息增益值的计算,然后将信息增益值最大的特征作为优先进行分支的节点。
计算信息增益的公式如下:
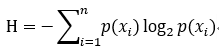
其中p(xi)为事件发生的概率。
2、信息增益的python实现
既然得到了信息增益的计算公式,那么这里就用python写一个函数来实现它,数据集采取二当中的例子。
以下函数实现了信息增益的计算:
def calcShannonEnt(dataSet):#入参是一个数据集 numEntries = len(dataSet)#首先取得数据集中的数据个数 labelCounts = {}#标签的集 for featVec in dataSet: #得到每一个数据的标记值 currentLabel = featVec[-1] #取得最后一列的标记值 if currentLabel not in labelCounts.keys(): #如果该标记没有被存到标记集合当中 labelCounts[currentLabel] = 0 #计算该标记的哈希值记录到标记集当中并赋值为0 labelCounts[currentLabel] += 1 #对该标记的数量加一 shannonEnt = 0.0 #初始信息增益为0 for key in labelCounts: #依次遍历每一个标记 prob = float(labelCounts[key])/numEntries #得到该标记的概率值 shannonEnt -= prob * log(prob,2) #求得信息增益 return shannonEnt
知道了怎么计算信息增益,就可以通过信息增益来对节点的顺序进行选择,进一步构造出一棵决策树。
四、 构造决策树
总的来说,构造决策树是一个递归的过程,首先通过计算信息增益取出一个特征作为判断的节点,然后将取出该特征的剩余数据集继续循环提取特征。
1、首先给出一个函数,该函数的作用是提取给定特征值为给定值的所有数据的数据集。
def splitDataSet(dataSet, axis, value):#按照指定特征划分数据集,dataset为给定数据集,axis为要筛选的特征,value为该特征的值 retDataSet = [] #被划分后的数据集 for featVec in dataSet: #遍历数据集中的每一个数据 if featVec[axis] == value: #找到数据集当中特征值为设置的值的数据 reducedFeatVec = featVec[:axis] #提取该特征之前的元素 reducedFeatVec.extend(featVec[axis+1:]) #提取该特征之后的元素 retDataSet.append(reducedFeatVec) #将该数据加入到要返回的数据集当中 return retDataSet
2、然后是一个在给定数据集当中计算出信息增益最大的特征的函数,以此来筛选特征:
def chooseBestFeatureToSplit(dataSet): #获取数据集中的最佳分支特征 numFeatures = len(dataSet[0]) - 1 #获取特征数量 baseEntropy = calcShannonEnt(dataSet) #计算基础熵 bestInfoGain = 0.0 #设置基础最佳信息增益为0 bestFeature = -1 #最佳特征索引 for i in range(numFeatures): #依次遍历每一个特征 featList = [example[i] for example in dataSet] #获取属于该特征的一列数据 uniqueVals = set(featList) #将数据列转换为set,过滤重复值 newEntropy = 0.0 #临时记录信息增益 for value in uniqueVals: #对数据列的每个值进行遍历 subDataSet = splitDataSet(dataSet, i, value) #根据每个值分别进行划分 prob = len(subDataSet)/float(len(dataSet)) #计算信息增益 newEntropy += prob * calcShannonEnt(subDataSet) #计算并累加信息增益 infoGain = baseEntropy - newEntropy if(infoGain > bestInfoGain): #求得信息增益最大的特征 bestInfoGain = infoGain bestFeature = i return bestFeature
3、可以筛选特征之后,就可以进行递归的构造决策树了:
def createTree(dataSet, labels): #通过给定的数据集以及标签构造决策树 classList = [example[-1] for example in dataSet] #取出数据集中的最后一列标记列 if classList.count(classList[0]) == len(classList): #如果标记的值只有一种,直接不用决策了 return classList[0] if len(dataSet[0]) == 1: #如果数据集只有一列,即可以到了最后决策阶段 return majorityCnt(classList) bestFeat = chooseBestFeatureToSplit(dataSet) #选出特征最为划分依据 bestFeatLabel = labels[bestFeat] myTree = {bestFeatLabel:{}} # 将该特征放到树的节点当中 del(labels[bestFeat]) #在标签集当中去掉该标签 featValues = [example[bestFeat] for example in dataSet] #取出属于该特征的所有可能取值 uniqueVals = set(featValues) #转换为set过滤重复值 for value in uniqueVals: #通过该特征的不同取值对决策树进行分支 subLabels = labels[:] #提取出剩余的标签集 myTree[bestFeatLabel][value] = createTree(splitDataSet (dataSet, bestFeat, value), subLabels) #递归构造决策树 return myTree
五、使用决策树。
此处使用依然是一个函数来使用我们定义好的决策树:
def classify(inputTree, featLabels, testVec): #三个参数分别是输入的决策树,特征集,进行预测的数据 firstStr = list(inputTree.keys())[0] #首先取出第一个分支特征 secondDict = inputTree[firstStr] # featIndex = featLabels.index(firstStr) for key in secondDict.keys():#根据该特征节点进行划分 if testVec[featIndex] == key: #如果待预测的数据的值 if type(secondDict[key]).__name__==‘dict‘: #如果是字典,则递归决策 classLabel = classify(secondDict[key], featLabels, testVec) else: #不然就直接得出预测结论 classLabel = secondDict[key] return classLabel
六、总结
决策树是一种相对基础而简单的预测算法,其中还有一些相关的剪枝和图的绘制等没有在本文中提到的知识,此处是对决策树进行一个最简单的介绍,如有不足,请多指教。
以上是关于机器学习实战之一---简单讲解决策树的主要内容,如果未能解决你的问题,请参考以下文章