机器学习实战——决策树
Posted WHJ226
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习实战——决策树相关的知识，希望对你有一定的参考价值。
目录
1 决策树训练和可视化
下面简单看一下例子：
常规模块的导入以及图像可视化的设置：
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier,export_graphviz
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)
#可视化决策树
#网站显示结构：http://webgraphviz.com/
#http://dreampuf.github.io/GraphvizOnline/将dot文件内容复制该网站即可，等待一会出图
export_graphviz(tree_clf,out_file="iris1_tree.dot")
默认路径下打开iris1_tree.dot文件：
digraph Tree
node [shape=box, fontname="helvetica"] ;
edge [fontname="helvetica"] ;
0 [label="X[0] <= 2.45\\ngini = 0.667\\nsamples = 150\\nvalue = [50, 50, 50]"] ;
1 [label="gini = 0.0\\nsamples = 50\\nvalue = [50, 0, 0]"] ;
0 -> 1 [labeldistance=2.5, labelangle=45, headlabel="True"] ;
2 [label="X[1] <= 1.75\\ngini = 0.5\\nsamples = 100\\nvalue = [0, 50, 50]"] ;
0 -> 2 [labeldistance=2.5, labelangle=-45, headlabel="False"] ;
3 [label="gini = 0.168\\nsamples = 54\\nvalue = [0, 49, 5]"] ;
2 -> 3 ;
4 [label="gini = 0.043\\nsamples = 46\\nvalue = [0, 1, 45]"] ;
2 -> 4 ;
具体可视化步骤已在本篇博文中讲述：
机器学习（18）——分类算法（补充）_WHJ226的博客-CSDN博客
简单步骤如下：首先打开该网站Graphviz Online ，最后将dot文件内容复制粘贴左侧代码区即可。
效果如下：（另外pycharm中的插件也可以实现决策树可视化，不过目前上述方法还没出现问题就未曾探索）
2 做出预测
假设我们找到了一朵鸢尾花，想要归类，那么从根节点（深度0，顶部）开始：这朵花的花瓣长度是否小于2.45CM？如果是，则向下移动到根的左侧子节点（深度1，左） 。在上面的例子中，这是一个叶节点（即没有任何子节点），所以不在继续，直接查看预测类别。
我们找到的另一朵鸢尾花，花瓣长度大于2.45厘米。这次我们需要移动到根节点的右侧子节点（深度1，右），由于该节点不是叶节点，所以它提出另一个问题：花瓣宽度是否小于1.75CM? 然后再做出预测。
节点的samples属性统计它应用的训练实例数量。例如，有100个训练实例的花瓣长度大于2.45cm（深度1，右），其中54个花瓣宽度小于1.75cm（深度2，左）。节点的value属性说明了该节点上每个类别的训练实例数量：例如，右下节点应用在0个Setoca鸢尾花、1个Versicolor鸢尾花和45个Virginica鸢尾花实例上。节点的gini属性衡量其不纯度：如果应用的所有训练实例都属于同一个类别，那么节点就是“纯”的（gini=0）.例如，深度1左侧节点仅应用于Setoca鸢尾花训练实例，所以它就是纯的，并且gini=0。下面的基尼不纯度公式将说明第i个节点的基尼系数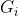 
的计算方式。
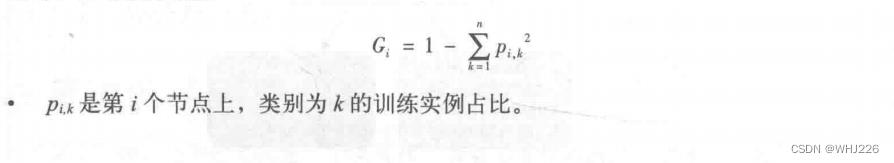
例如，深度2左侧节点，基尼系数等于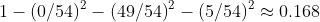 
。
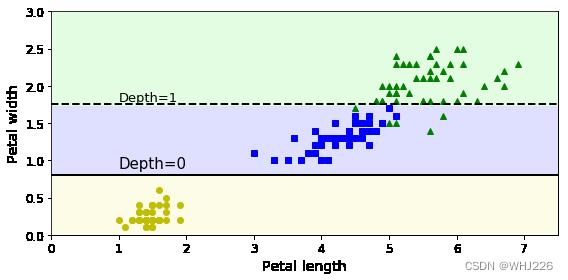
下图是决策树的决策边界。加粗直线表示根节点（深度0）的决策边界：花瓣长度=2.45厘米。因为左侧区域是纯的（只有Setoca鸢尾花），所以不可再分。右侧区域不是纯的，所以深度1右侧的节点在花瓣宽度=1.75厘米处（虚线表示）再次分离。此处最大深度max_depth 设置为2，所以决策树在此停止。但若max_depth 设置为3，那么两个深度为2的节点将各自再产生一条决策边界（点线表示）。
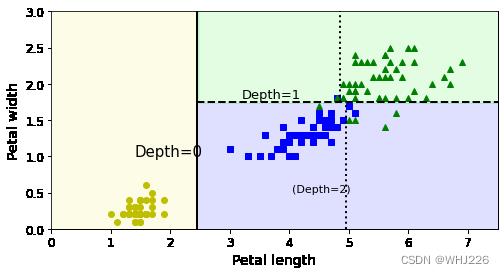
代码实现如下：
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if not iris:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
if plot_training:
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", label="Iris-Virginica")
plt.axis(axes)
if iris:
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
else:
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
if legend:
plt.legend(loc="lower right", fontsize=14)
plt.figure(figsize=(8, 4))
plot_decision_boundary(tree_clf, X, y)
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.40, 1.0, "Depth=0", fontsize=15)
plt.text(3.2, 1.80, "Depth=1", fontsize=13)
plt.text(4.05, 0.5, "(Depth=2)", fontsize=11)
plt.show()3 估算类别概率
决策树同样可以估算某个实例属于特定类别k的概率：首先，我们跟随决策树找到该实例的叶节点，然后返回该节点中类别k的训练实例占比。例如，我们发现一朵鸢尾花，花瓣长5厘米，宽1.5厘米。相应的叶节点为深度2左侧节点，因此决策树输出如下概率：Setoca鸢尾花，0%（0/54）；Versicolor鸢尾花，90.7%（49/54）；Virginica鸢尾花，9.3%（5/54）。
代码展示：
tree_clf.predict_proba([[5, 1.5]])运行结果如下：
array([[0. , 0.90740741, 0.09259259]])预测类别：
tree_clf.predict([[5, 1.5]])运行结果如下：
array([1])4 CART训练算法
分类与回归树（Classification And Regression Tree，简称CART）：首先，使用单个特征k和阈值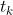
（例如，花瓣长度≤2.45厘米）将训练集分成两个子集。k和阈值 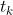：是产生出最纯子集（受其大小加权）的 k和阈值 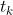就是经算法搜索确定的（
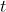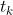,）。算法尝试最小化的成本函数公式如下：
一旦成功将训练集一分为二，它将使用相同的逻辑，继续分裂子集，然后是子集的子集，依次循环递进。直到抵达最大深度（超参数 max_depth 控制） ，或是再也找不到能够降低不纯度的分裂，它才会停止。
注意，CART是一种贪婪算法：从顶层开始搜索最优分裂，然后每层重复这个过程。几层分裂之后，它不会检视这个分裂的不纯度是否为可能的最低值。通常会产生一个相当不错的解，但不能保证是最优解。
5 正则化超参数
决策树极少对训练数据作出假设。如果不加以限制，树的结构将跟随训练集变化，有可能出现过度拟合。这种模型通常被称为非参数模型，不是说它不包含任何参数，而是指在训练之前没有确定参数的数量，导致模型结构自由而紧密地贴近数据。未避免过度拟合，需要在训练过程中降低决策树的自由度，这个过程就是正则化。Scikit-Learn中，这由超参数 max_depth 控制。减小max_depth可使模型正则化，从而降低过度拟合的风险。
DecisionTreeClassifier 也有一些参数，可以限制决策树的形状：min_samples_split （分裂前节点必须有的最小样本数）、 min_samples_leaf（叶节点必须有的最小样本数量）、 min_weight_fraction_leaf（同min_samples_leaf，但表现为加权实例总数的占比）、 max_leaf_nodes（最大叶节点数量）、 max_features（分裂每个节点评估的最大特征数量）。 增大超参数min_* 或减小 max_* 将使模型正则化。
其实，我们还可以先不加约束的训练模型，然后再对不必要的节点进行删除。如果一个节点的子节点全部为叶节点，则该节点可被认为不必要，除非它所表示的纯度提升有重要的统计意义。标准统计测试，比如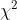 
测试，用来估算“提升纯粹是处于偶然” （被称为虚假设）的概率。如果这个概率（称之为p值）高于一个给定阈值（通常为5%，超参数控制），那么这个节点可被认为不必要，其子节点可被删除。
下图显示的是在卫星数据集上训练的两个决策树。左图使用默认参数（无约束）来训练决策树，右图的决策树应用 min_samples_leaf=4 进行训练。
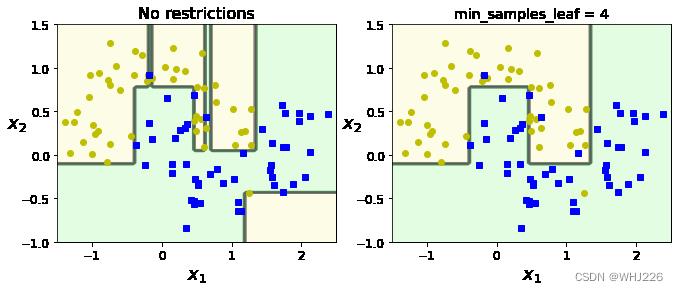
很明显，左图模型过度拟合，右图泛化效果好。
代码实现如下：
from sklearn.datasets import make_moons
Xm, ym = make_moons(n_samples=100, noise=0.25, random_state=53)
deep_tree_clf1 = DecisionTreeClassifier(random_state=42)
deep_tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4, random_state=42)
deep_tree_clf1.fit(Xm, ym)
deep_tree_clf2.fit(Xm, ym)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_decision_boundary(deep_tree_clf1, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("No restrictions", fontsize=16)
plt.subplot(122)
plot_decision_boundary(deep_tree_clf2, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("min_samples_leaf = ".format(deep_tree_clf2.min_samples_leaf), fontsize=14)
plt.show()6 回归
我们可以使用Scikit-Learn的 DecisionTreeRegressor 来构建一个回归树。下面我们在一个带有噪声的二次数据集上进行训练，其中max_depth = 2 ：
# Quadratic training set + noise
np.random.seed(42)
m = 200
X = np.random.rand(m, 1)
y = 4 * (X - 0.5) ** 2
y = y + np.random.randn(m, 1) / 10
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X, y)
export_graphviz(tree_reg,out_file="random_tree.dot")结果如下：
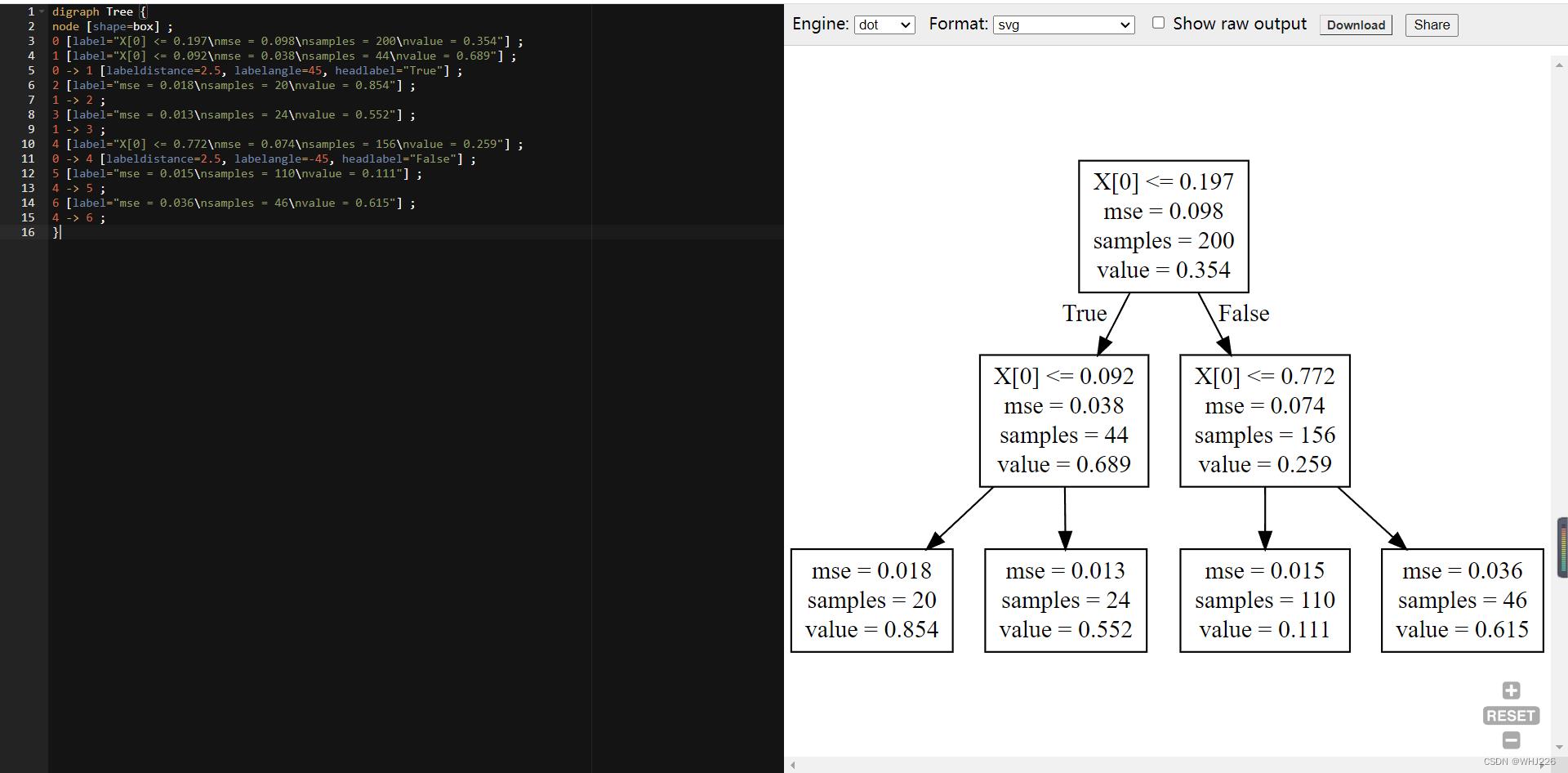
这棵树与之前的差别在于，每个节点上不再是预测一个类别而是预测一个值。假设，我们想对一个x1=0.6的新实例进行预测，最后到达value=0.111的叶节点。该预测结果其实就是与这个叶节点关联的110个实例的平均目标值。在这110个实例上，预测产生的均方根误差为0.015。
下图显示了该模型的预测。如果设置max_depth=3，将得到右图预测。注意，每个区域的的预测值永远等于该区域内实例的目标平均值。算法分裂每个区域的方法，就是使最多的训练实例尽可能接近这个预测值。
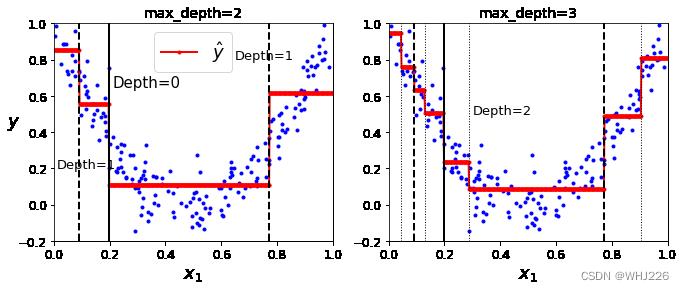
代码实现如下：
tree_reg1 = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)
def plot_regression_predictions(tree_reg, X, y, axes=[0, 1, -0.2, 1], ylabel="$y$"):
x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1)
y_pred = tree_reg.predict(x1)
plt.axis(axes)
plt.xlabel("$x_1$", fontsize=18)
if ylabel:
plt.ylabel(ylabel, fontsize=18, rotation=0)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\\haty$")
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_regression_predictions(tree_reg1, X, y)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
plt.plot([split, split], [-0.2, 1], style, linewidth=2)
plt.text(0.21, 0.65, "Depth=0", fontsize=15)
plt.text(0.01, 0.2, "Depth=1", fontsize=13)
plt.text(0.65, 0.8, "Depth=1", fontsize=13)
plt.legend(loc="upper center", fontsize=18)
plt.title("max_depth=2", fontsize=14)
plt.subplot(122)
plot_regression_predictions(tree_reg2, X, y, ylabel=None)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
plt.plot([split, split], [-0.2, 1], style, linewidth=2)
for split in (0.0458, 0.1298, 0.2873, 0.9040):
plt.plot([split, split], [-0.2, 1], "k:", linewidth=1)
plt.text(0.3, 0.5, "Depth=2", fontsize=13)
plt.title("max_depth=3", fontsize=14)
plt.show()CART算法的工作原理跟前面介绍的大致相同，唯一不同在于，它分类训练集的方式不是最小化纯度，而是最小化MSE。下面的公式为该算法尝试最小化的成本函数。
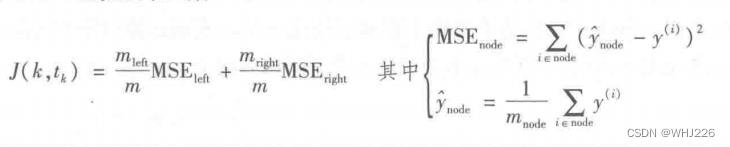
前面我们曾说过决策树过度拟合。如果没有任何正则化（即使用默认超参数），我们将得到下图所示的预测结果，显然左图出现了过度拟合。 我们可以通过设置 min_samples_leaf=10 ，得到一个看起来合理的模型，右图所示。
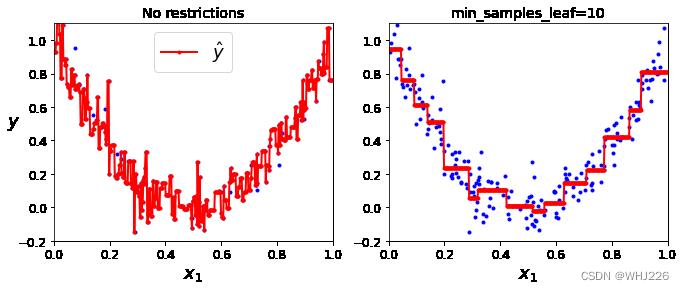
代码实现如下：
tree_reg1 = DecisionTreeRegressor(random_state=42)
tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf=10)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)
x1 = np.linspace(0, 1, 500).reshape(-1, 1)
y_pred1 = tree_reg1.predict(x1)
y_pred2 = tree_reg2.predict(x1)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\\haty$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", fontsize=18, rotation=0)
plt.legend(loc="upper center", fontsize=18)
plt.title("No restrictions", fontsize=14)
plt.subplot(122)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred2, "r.-", linewidth=2, label=r"$\\haty$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.title("min_samples_leaf=".format(tree_reg2.min_samples_leaf), fontsize=14)
plt.show()7 不稳定性
你可能注意到，决策树青睐正交的决策边界（所有分裂都与轴线垂直），因此他们对训练集的旋转非常敏感。下图是一个简单的线性可分离数据集：左图中决策树可以轻松分裂，右图中，数据集旋转了45°后，决策边界产生了不必要的卷曲。这也导致右侧模型可能泛化不佳。限制这种问题的方法之一就是用PCA。
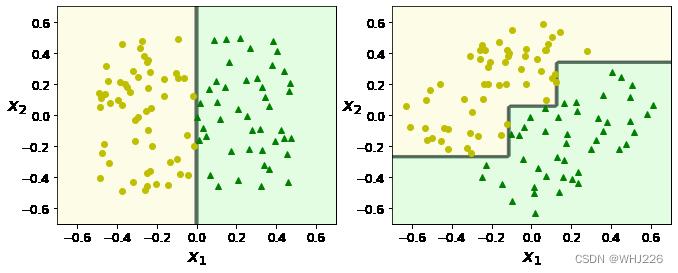
代码实现如下：
np.random.seed(6)
Xs = np.random.rand(100, 2) - 0.5
ys = (Xs[:, 0] > 0).astype(np.float32) * 2
angle = np.pi / 4
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
Xsr = Xs.dot(rotation_matrix)
tree_clf_s = DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs, ys)
tree_clf_sr = DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr, ys)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_decision_boundary(tree_clf_s, Xs, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
plt.subplot(122)
plot_decision_boundary(tree_clf_sr, Xsr, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
plt.show()更概括的说，决策树的主要问题是它们对训练数据中的小变化非常敏感。例如，我们从鸢尾花数据集中移除花瓣最宽的Versicolor鸢尾花（花瓣长4.8厘米，宽1.8厘米），然后我们重新训练一个决策树，将得到下图模型。
事实上，由于Scikit-Learn所使用的算法是随机的，如果我们想要得到相同的模型，需要对超参数random_state 进行设置。
学习笔记——《机器学习实战：基于Scikit-Learn和TensorFlow》
以上是关于机器学习实战——决策树的主要内容，如果未能解决你的问题，请参考以下文章
机器学习决策树（划分选择算法流程剪枝处理，连续值与缺失值处理）