浅谈可持久化数据结构

Posted 2020-12-28 cjjsb

Preface

由于我真的是太弱了，所以真的是浅谈。

神奇的数据结构其实我也很虚啊！

---

值域线段树

简单的说，值域线段树区间里面存的是在这个区间内的数的个数有多少个。

有没有感觉很简单，考虑一下如果我们有一棵这样的线段树，查找排名为rk的数时只需要看一下左子树的大小就可以判断在左边还是右边了。

有没有感觉很像BST

---

动态开点与可持久化

根据上面的值域线段树，我们可以得出一种naive的做法：

对于每一个前缀([1,i](iin[1,n]))都开一棵值域线段树，然后查询区间的时候直接每个节点的size都变成(size(r)-size(l-1))，就是把前缀和的思想搬到了树上

然后不仅要MLE，每次复制线段树都T了

我们考虑优化一波，我们发现每一次操作只会改变从根节点到叶子节点的一条路径上点的值。

然后由于线段树的深度是稳定且均匀的(logn)，因此我们发现许多节点的信息都是可以共用的：

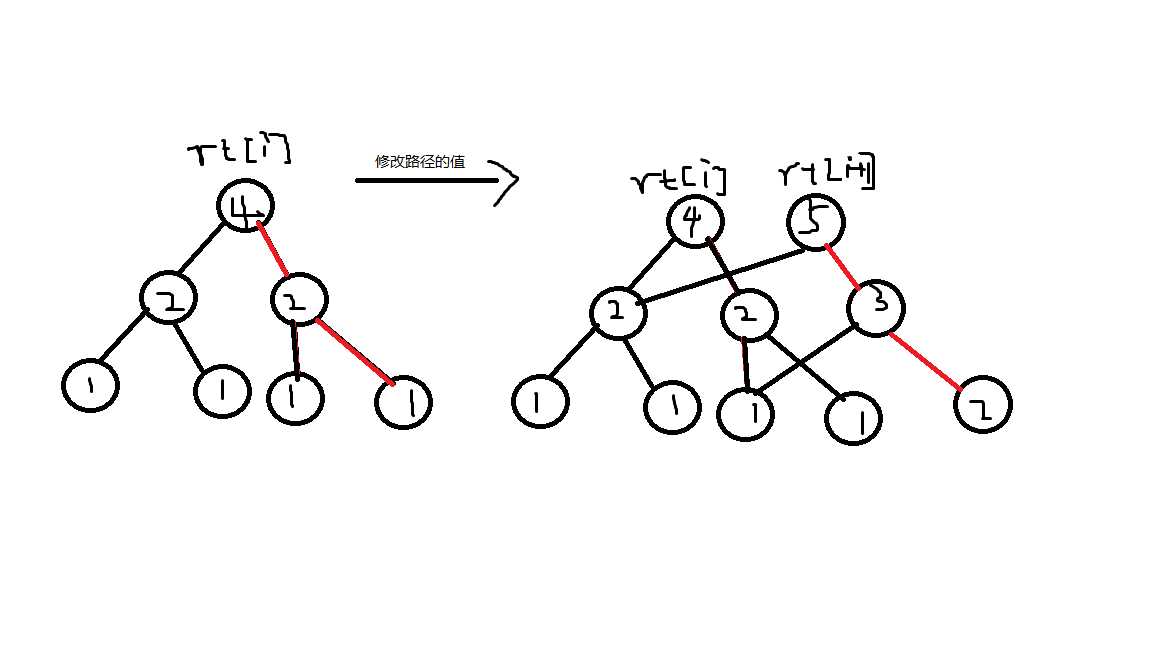
我们在修改红色的这一条路径的信息时，我们把这一条链上的点都新建一个分身并和原图保持一样的形状。

我们在每一次操作后都记录当前的根节点的编号即可。这就是传说中的可持久化，因为我们成功地保存了历史版本。

当然，这样的线段树不可能保持固定的形态，因此我们记录每一个点的左右儿子的信息。然后每次更新时再开新的节点，这就是动态开点（平衡树写多的话就完全没问题）

---

实现主席树

看板子题Luogu P3834 【模板】可持久化线段树 1（主席树）

首先值域线段树不能处理那么大的数字，因此我们先离散化

然后大体的做法上面都讲了，直接上CODE吧

#include<cstdio>
#include<cctype>
#include<algorithm>
using namespace std;
const int N=2e5+5;
struct President_tree//President总统，不知道有没有主席的意思
{
    int lc,rc,sum;
}node[N<<6];
int n,m,q,a[N],b[N],l,r,k,rt[N],tot;
inline char tc(void)
{
    static char fl[100000],*A=fl,*B=fl;
    return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
    x=0; char ch; int flag=1; while (!isdigit(ch=tc())) flag=ch^‘-‘?1:-1;
    while (x=(x<<3)+(x<<1)+ch-‘0‘,isdigit(ch=tc())); x*=flag;
}
inline void write(int x)
{
    if (x>9) write(x/10);
    putchar(x%10+‘0‘);
}
inline int find(int x)
{
    int l=1,r=m;
    while (l<=r)
    {
        int mid=l+r>>1;
        if (b[mid]==x) return mid;
        if (b[mid]<x) l=mid+1; else r=mid-1;
    }
}
inline void build(int &now,int l,int r)//建树，注意动态开点
{
    now=++tot;
    if (l==r) return;
    int mid=l+r>>1;
    build(node[now].lc,l,mid); build(node[now].rc,mid+1,r);
}
inline int modify(int lst,int l,int r,int id)//更新某段路径的值
{
    int now=++tot; node[now]=node[lst]; ++node[now].sum;
    if (l==r) return now;
    int mid=l+r>>1;
    if (id<=mid) node[now].lc=modify(node[lst].lc,l,mid,id);
    else node[now].rc=modify(node[lst].rc,mid+1,r,id); return now;
}
inline int query(int u,int v,int l,int r,int k)//查询区间第k小，这里直接同时跳两条路径了
{
    int mid=l+r>>1,dlt=node[node[v].lc].sum-node[node[u].lc].sum;
    if (l==r) return l;
    if (dlt>=k) return query(node[u].lc,node[v].lc,l,mid,k);
    else return query(node[u].rc,node[v].rc,mid+1,r,k-dlt);
}
int main()
{
    //freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
    register int i; read(n); read(q);
    for (i=1;i<=n;++i)
    read(a[i]),b[i]=a[i];
    sort(b+1,b+n+1); m=unique(b+1,b+n+1)-b-1; build(rt[0],1,m);
    for (i=1;i<=n;++i)
    rt[i]=modify(rt[i-1],1,m,find(a[i]));
    for (i=1;i<=q;++i)
    {
        read(l); read(r); read(k);
        write(b[query(rt[l-1],rt[r],1,m,k)]); putchar(‘
‘);
    }
    return 0;
}

---

实现可持久化数组

板子题：P3919 【模板】可持久化数组（可持久化线段树/平衡树）

这个就更加简单了，我们相当于维护一个可持久化线段树，并支持单点修改，单点查询即可

是不是听起来很ZZ，感觉完全不需要线段树

不过线段树起到了良好的存储信息+快速查找的左右，因此是不二选择（当然你要非旋Treap我也不想管你）

CODE

#include<cstdio>
#include<cctype>
#include<algorithm>
using namespace std;
const int N=1e6+5;
struct Persistence_segtree//Persistence-这个是可持久化的意思
{
    int lc,rc,x;
}node[N*20];
int n,m,a[N],rt[N],opt,x,y,id,tot;
inline char tc(void)
{
    static char fl[100000],*A=fl,*B=fl;
    return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
    x=0; char ch; int flag=1; while (!isdigit(ch=tc())) flag=ch^‘-‘?1:-1;
    while (x=(x<<3)+(x<<1)+ch-‘0‘,isdigit(ch=tc())); x*=flag;
}
inline void write(int x)
{
    if (x<0) putchar(‘-‘),x=-x;
    if (x>9) write(x/10); putchar(x%10+‘0‘);
}
inline void build(int &now,int l,int r)
{
    now=++tot; if (l==r) { node[now].x=a[l]; return; }
    int mid=l+r>>1; build(node[now].lc,l,mid); build(node[now].rc,mid+1,r);
}
inline int modify(int lst,int l,int r,int id,int x)
{
    int now=++tot; node[now]=node[lst];
    if (l==r) { node[now].x=x; return now; } int mid=l+r>>1;
    if (id<=mid) node[now].lc=modify(node[lst].lc,l,mid,id,x);
    else node[now].rc=modify(node[lst].rc,mid+1,r,id,x); return now;
}
inline int query(int now,int l,int r,int id)
{
    if (l==r) return node[now].x; int mid=l+r>>1;
    if (id<=mid) return query(node[now].lc,l,mid,id);
    else return query(node[now].rc,mid+1,r,id);
}
int main()
{
    //freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
    register int i; read(n); read(m);
    for (i=1;i<=n;++i) read(a[i]); build(rt[0],1,n);
    for (i=1;i<=m;++i)
    {
        read(x); read(opt); read(id);
        if (opt^2) read(y),rt[i]=modify(rt[x],1,n,id,y); 
        else write(query(rt[i]=rt[x],1,n,id)),putchar(‘
‘);
    }
    return 0;
}

---

实现可持久化并查集

这个是最烦人的操作了吧，理论上只需要可持久化数组就可以搞了。

首先我们要摒弃掉平时的那些关于并查集的想法，在可持久化并查集中，不可以路径压缩。

那么还不GG，直接搞不是爆炸？

其实还有一个优化叫做按秩合并，也是启发式合并的一种，就是记录一下每个联通块的大小，然后每次合并的时候把小的并到大的上面去即可

复杂度最差(O(n log n)) ，完全不虚的好不好。

CODE

#include<cstdio>
#include<cctype>
using namespace std;
const int N=200005;
struct President_tree
{
    int ch[2],fa,dep;
}node[N*20];
int n,m,opt,x,y,rt[N],tot;
inline char tc(void)
{
    static char fl[100000],*A=fl,*B=fl;
    return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
    x=0; char ch; while (!isdigit(ch=tc()));
    while (x=(x<<3)+(x<<1)+ch-‘0‘,isdigit(ch=tc()));
}
inline void swap(int &a,int &b)
{
    int t=a; a=b; b=t;
}
inline void build(int &now,int l,int r)
{
    now=++tot; if (l==r) { node[now].fa=l; return; }
    int mid=l+r>>1; build(node[now].ch[0],l,mid); build(node[now].ch[1],mid+1,r);
}
inline void insert(int lst,int &now,int l,int r,int x,int fa)
{
    now=++tot; if (l==r) { node[now].fa=fa; node[now].dep=node[lst].dep; return; } 
    int mid=l+r>>1; node[now].ch[0]=node[lst].ch[0]; node[now].ch[1]=node[lst].ch[1];
    if (x<=mid) insert(node[lst].ch[0],node[now].ch[0],l,mid,x,fa);
    else insert(node[lst].ch[1],node[now].ch[1],mid+1,r,x,fa);
}
inline void updata(int now,int l,int r,int x)
{
    if (l==r) { ++node[now].dep; return; } int mid=l+r>>1;
    if (x<=mid) updata(node[now].ch[0],l,mid,x);
    else updata(node[now].ch[1],mid+1,r,x);
}
inline int query(int now,int l,int r,int x)
{
    if (l==r) return now; int mid=l+r>>1;
    if (x<=mid) return query(node[now].ch[0],l,mid,x);
    else return query(node[now].ch[1],mid+1,r,x);
}
inline int getfather(int t,int x)
{
    int fa=query(t,1,n,x);
    return x^node[fa].fa?getfather(t,node[fa].fa):fa;
}
inline void unionn(int t,int x,int y)
{
    rt[t]=rt[t-1]; int fx=getfather(rt[t],x),fy=getfather(rt[t],y);
    if (node[fx].fa==node[fy].fa) return;
    if (node[fx].dep<node[fy].dep) swap(fx,fy);
    insert(rt[t-1],rt[t],1,n,node[fy].fa,node[fx].fa);
    if (node[fx].dep==node[fy].dep) updata(rt[t],1,n,node[fx].fa);
}
inline void check(int t,int x,int y)
{
    rt[t]=rt[t-1]; int fx=getfather(rt[t],x),fy=getfather(rt[t],y);
    puts(node[fx].fa^node[fy].fa?"0":"1");
}
int main()
{
    //freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
    register int i; read(n); read(m); build(rt[0],1,n);
    for (i=1;i<=m;++i)
    {
        read(opt); read(x);
        switch (opt)
        {
            case 1:read(y),unionn(i,x,y);break;
            case 2:rt[i]=rt[x];break;
            case 3:read(y),check(i,x,y);break;
        }
    }
    return 0;
}

PS：刚开始swap写错了害我调了2H+