可持久化线段树--主席树

Posted 2022-11-16 -ackerman

浅谈可持久化线段树--主席树

权值线段树

权值线段树和普通线段树不一样的地方就是在于 它的结点存储的是区间内数的个数

这个线段树的好处就在于我们可以根据 左子树 和 右子树 的大小从而进行 查找某个数的排名 或者 查找排名为rk的数

 

可持久化的含义

可持久数据结构主要指的是我们可以查询历史版本的情况并支持插入，利用使用之前历史版本的数据结构来减少对空间的消耗（能够对历史进行修改的是函数式）。 

 

主席树的建树过程：

最开始的时候就是一个空树

 

 

 

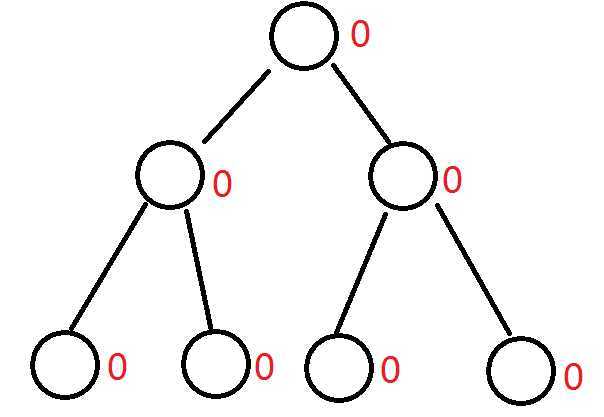
然后我们再插入一个元素3

 

 

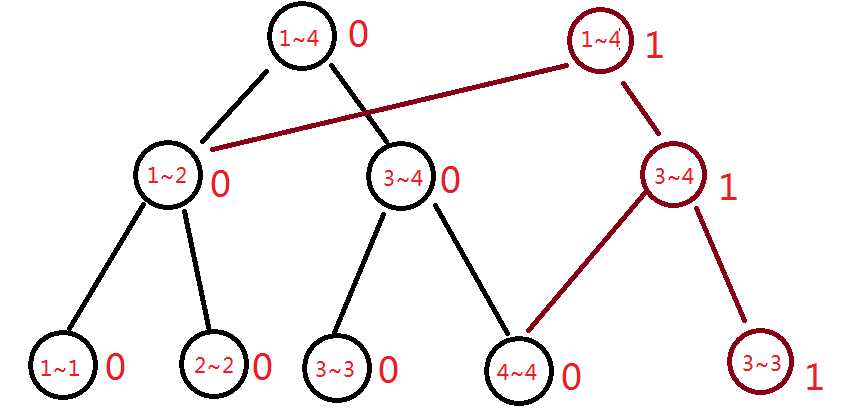
再加入一个元素 1

 

 

 

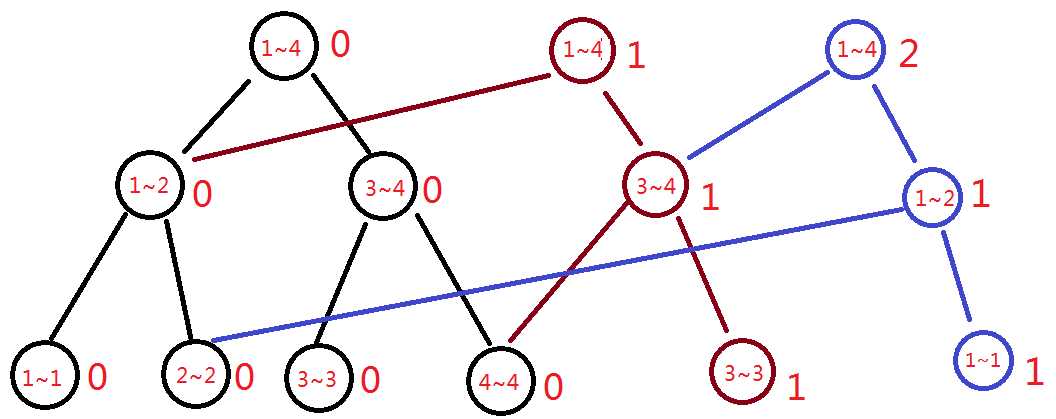
模版一 ：求区间第K大

 

我们考虑查询。

例如我们插入： 1 5 2 6 3 7 4

要查询[2, 5]中第3大的数我们首先把第1棵线段树和第5棵拿出来。

 

根据前面说的插入操作 我们最终得到的线段树是这样的：

 

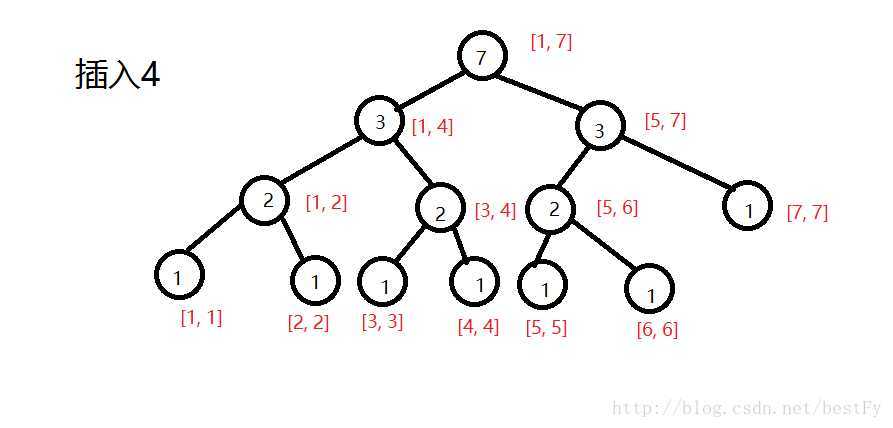
 要查询[2, 5]中第3大的数我们首先把第1棵线段树和第5棵拿出来。

 

 

 

 

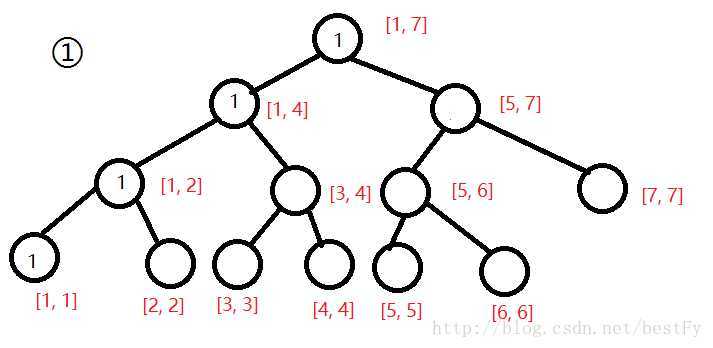
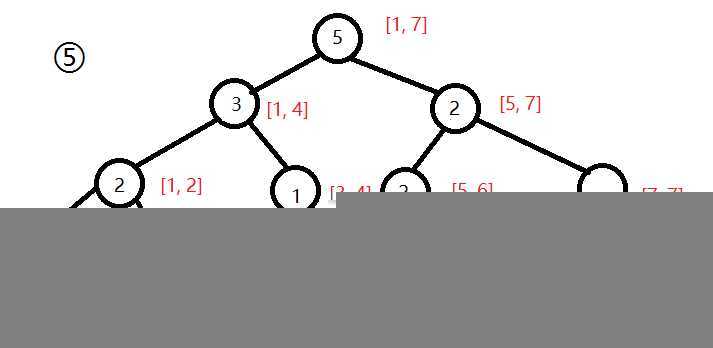
然后我们发现，将对应节点的数相减，刚刚好就是[2, 5]内某个范围内的数的个数。比如[1, 4]这个节点相减是2，就说明[2. 5]内有2个数是在1~4范围内（就是2, 3）。

所以对于一个区间[l, r]，我们可以每次算出在[l, mid]范围内的数，如果数量>=k（k就是第k大），就往左子树走，否则就往右子树走。

 

 1 #include <stdio.h>
 2 #include <iostream>
 3 #include <algorithm>
 4 #include <string.h>
 5 #include <vector>
 6 #include <random>
 7 
 8 const int maxn = 2e5 + 10;
 9 
10 int ls[maxn<<5],rs[maxn<<5],sum[maxn<<5],rt[maxn<<5];
11 int cnt;
12 
13 void init() 
14     memset(sum,0, sizeof(sum));
15     cnt  = 0;
16 
17 int build(int l, int r)
18     int root = ++ cnt;
19     if(l == r) return root;
20     int mid = (l + r) >> 1;
21     ls[root] = build(l, mid);
22     rs[root] = build(mid + 1, r);
23     return root;
24 
25 int update(int k, int l, int r, int root)
26     int id = ++ cnt;
27     ls[id] = ls[root]; rs[id] = rs[root]; sum[id] = sum[root] + 1;
28     if(l == r) return id;
29     int mid = (l + r) >> 1;
30     if(k <= mid) ls[id] = update(k, l, mid, ls[id]);
31     if(k > mid) rs[id] = update(k, mid + 1, r, rs[id]);
32     return id;
33 
34 int query(int k, int u, int v, int l, int r)
35 
36     int mid = (l + r) >> 1;
37     int x = sum[ls[v]] - sum[ls[u]];
38     if(l == r) return l;
39     if(k <= x) return query(k, ls[u], ls[v], l, mid);
40     if(k > x) return query(k - x, rs[u], rs[v], mid + 1, r);
41 
42 
43 std::vector<int> v;
44 int getid(int x) 
45     return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
46 
47 
48 int arr[maxn];
49 int main() 
50     int n,m;
51     scanf("%d%d",&n,&m);
52     for (int i=1;i<=n;i++) 
53         scanf("%d",&arr[i]);
54         v.push_back(arr[i]);
55     
56     std::sort(v.begin(),v.end());
57     v.erase(std::unique(v.begin(),v.end()),v.end());
58     int len = v.size();
59     rt[0] = build(1,len);
60     for (int i=1;i<=n;i++) 
61         rt[i] = update(getid(arr[i]),1,len,rt[i-1]);
62     
63     while (m--) 
64         int l,r,k;
65         scanf("%d%d%d",&l,&r,&k);
66         printf("%d\\n",v[query(k,rt[l-1],rt[r],1,len)-1]);
67     
68