机器学习算法总结

Posted 2020-10-09

机器学习算法分为两种：有监督和无监督。简单来说，有监督是指输入数据有y值，希望学习完后能找到x和y值之间的关系；无监督是指仅有x值，希望能从x中提取出特征。

常见监督算法：线性回归，逻辑回归，支持向量机（support vector machine，SVM），k-最邻近（k-NearestNeighbor，KNN），决策树（decision tree）

常见无监督算法：主成分分析（principal components analysis，PCA），k-均值聚类

 

机器学习嘛，说白了就是从一组数据里面找出规律，然后用这个规律去预测那组数据以外的数据。比如我们现在知道了过去几天股市的收盘价，想从中找到规律，预测明天股市的价格。如果真的能找到，能就赚大发了。

那如何找这个规律呢？正常人第一反应肯定是且不说预测未知的数据， 这个规律至少能较准确地预测已知的数据，即模型预测的结果和已知数据差异最小。那怎么定义差异最小呢？数学家和概率学家各自给出了自己的方案：

1.在数学家的眼里，万物皆是数字。那么差异最小就是数据和预测值之间的差值最小。当有多个数据的时候，就是多个数据与多个预测值的差之和最小。由于这个差有正有负不好衡量，就统一平方后再求和。

2.在概率学家的眼里，万物皆有概率。那么差异最小可以翻译预测值是对应的数据的概率最大。那么好端端的数据怎么无缘无故变成了概率了呢？对于所有的数据（已知和未知的）来说，其中每一个数据的概率是多少呢？我们不知道，所以我们只能假设他们服从某些分布。那具体是什么分布呢？我的理解是，哪个分布计算时好算就用哪个分布。概率学家看到这会被气死。。。

举个栗子：

我们最常见的线性分布。我们有n个数据（x₁,x_2,...,x_n）和他们对应的观测值（y₁,y₂,...,y_n）,我们希望找到规律θ，使得θx_i尽可能的接近y_i。

对于数学家来讲，就是最小化∑ⁿ(y_i-x_i)²

对于概率学家来说，就是最大化各个点的概率。一般来讲，线性回归选的分布是高斯分布，为什么呢？等下解释。所以呢最后计算的公式为：

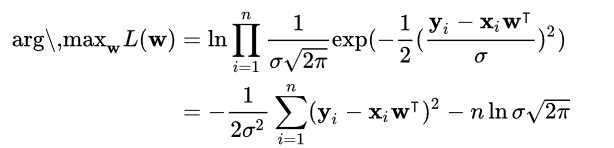
这里w就是θ。因为公式里面取对数，常数项σ,n,π都不影响结果，去掉后其实就是最大化 -∑ⁿ(y_i-x_i)²，也就是最小化∑ⁿ(y_i-x_i)²。所以回到上面为什么选高斯分布，我猜想的是可以看做由最小二乘法的反推∑ⁿ(y_i-x_i)²，最小二乘法反推回来像什么概率分布就用什么概率分布来估计。

笔者很懒，迟点回来再补充。。。。