模板时间◆模板·II◆ 树链剖分
Posted luckyglass-blog
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了模板时间◆模板·II◆ 树链剖分相关的知识,希望对你有一定的参考价值。
【模板·II】树链剖分
学长给我讲树链剖分,然而我并没有听懂,还是自学有用……另外感谢一篇Blog +by 自为风月马前卒+
一、算法简述
树链剖分可以将一棵普通的多叉树转为线段树计算,不但可以实现对一棵子树的操作,还可以实现对两点之间路径的操作,或是求 LCA(看起来很高级)。
其实树链剖分不算什么特别高难的算法,它建立在 LCA、线段树、DFS序 的基础上(如果不了解这些算法的还是先把这些算法学懂再看树链剖分吧 QwQ)。又因为树链剖分的基础算法不难,树链剖分的题也逐渐被引入 OI 赛中。
不得不说,它的代码很长……尽管很多都是模板,但是还是必须理解清楚每一个模板的含义,不然容易混淆。
二、原理
(1)基本定义
重儿子:对于每一个非叶子节点u的儿子vi,若以vi为根的子树的节点数是u的所有儿子的子树的节点数中最大的,则 vi 是u的重儿子;
重边:对于每一个非叶子节点u,它与其重儿子的连边为重边;
重链:树中只包含重边的一条链,这里我们把单个元素也看成重链;
轻儿子:非重儿子的节点;轻边:非重边;
举个例子:
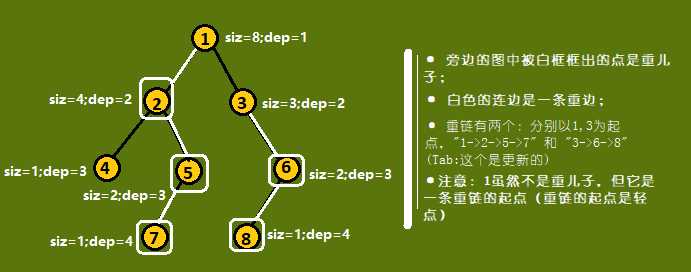
(2)简单定理
- 重链的起点一定是轻点;
- 一条轻边一定连接重链上的一点和另一条重链的起点(重链的起点算入重链);
- 任何节点都只属于一条重链;
- 除了叶子节点,其他所有点一定有重儿子;
(3)计算重儿子
siz[u]: 以u节点为根的子树的节点数量(包含u);
dep[u]:u的深度(根节点深度为1);
fa[u]:节点u的父亲,一般来说根节点父亲为0;
heavy[u]:u的重儿子,没有为0;
val[u]:u的点权;
(以上是我自己定义的名字,可能不太规范)
可以直接用一个DFS从根节点开始,用递归的方式求出每一棵子树的节点数,并找到有最大节点数的儿子,作为heavy[],不要在意那些节点数相同的情况,如果出现,则只选取其中一个作为heavy[]就可以了。
具体如何实现?我还是奉上代码吧 @( ? x ? )@:
1 void DFS1(int u,int Fa,int Dep) 2 { 3 dep[u]=Dep;fa[u]=Fa; //更新深度、父节点 4 siz[u]=1; //将u本身计入siz 5 int MAX_siz=0; //最大子树大小 6 for(int i=0;i<lnk[u].size();i++) 7 if(lnk[u][i]!=Fa) //避免重复错误 8 { 9 int v=lnk[u][i]; 10 DFS1(v,u,Dep+1); 11 siz[u]+=siz[v]; //统计大小 12 if(siz[v]>MAX_siz) 13 MAX_siz=siz[v],heavy[u]=v; //求重儿子 14 } 15 }
(4)计算DFN序以及重链
上一步的DFS1为求重链打下了基础。
新添几个定义: ID[u]:u的DFS序(或者可以叫dfn);Top[u]:u所在的重链的起始点(即深度最小的点);fval[x]:DFS序为x的点的点权;
这次DFS,我们需要改变搜索顺序,不能按输入顺序遍历点——先搜索重儿子,再搜索其它儿子,如果没有重儿子,说明是叶子节点,结束搜索后回溯。这样我们保证了对于每一个非叶子节点u和它的重儿子v,ID[u]和ID[v]是连续的,按照这个规律,我们可以发现,在同一条重链中,相邻元素的ID总是连续的。这是一个非常重要的性质,正因为有这个性质,我们可以应用线段树来计算(等会解释)。
举个例子吧:
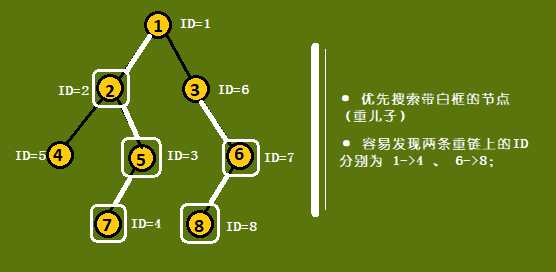
如何求 Top[u] 呢?
我们可以通过下传参数实现——下传一个参数 topf ,表示当前节点属于的重链起始于 topf。我们优先访问u的重儿子v,即使优先访问u所在的重链,此时u、v仍然属于同一个重链,因此topf不变,可以下传。而当我们搜索u的其他儿子v时,相当于经过了一条轻边,因此我们就到达了另一条重链的起点("简单定理"中第2条),所以将v作为topf继续下传。
1 void DFS2(int u,int topf) 2 { 3 ID[u]=++ID_cnt;fval[ID_cnt]=val[u]; //ID_cnt 就是当前的DFS序;同时给fval赋值 4 Top[u]=topf; 5 if(!heavy[u]) return; //叶子节点 6 DFS2(heavy[u],topf); 7 for(int i=0;i<lnk[u].size();i++) 8 { 9 int v=lnk[u][i]; 10 if(ID[v]) continue; //避免访问重复 11 DFS2(v,v); //v是另一条重链的起点 12 } 13 }
(5)线段树
这才是重头戏……
线段树最明显的优点就是区间修改、区间查询,但是这一切的前提就是它修改、查询的是一个连续的区间!这就是为什么要让一条重链上的ID成为连续的一串。在这棵线段树上,区间是ID值,即我们储存的是连续一段ID值所包含的信息。
但是这仅仅是第一步……谁也不知道线段树的强大功能到底还有哪些……
◆ 修改、查询一棵子树
一个最简单的性质 —— 以u为根的子树中 DFS 序(ID)是连续的长度为siz[u]的序列。当我们知道 ID[u] 时,我们可以马上知道这棵子树中ID最大的节点ID为 (ID[u]+siz[u]-1),又因为这是一个连续区间,线段树就可以发挥它的用途了!
以u为根的一棵子树在线段树上对应区间为 [ID[u],ID[u]+siz[u]-1]。
◆ 修改、查询从u到v的一条路径(当然也是唯一路径)
我们先分三种情况(在下面的描述中,dep[u]≤dep[v]):
① u、v本来就在一条重链上
由于重链是连续一段,且 dep[u]≤dep[v] ,所以 u->v 是连续的区间 [ID[u],ID[v]] ,这样用线段树求解比较容易吧。
② u、v分别属于的重链之间隔了一条轻边
还记得之前的“简单定理”吗?既然两条重链隔了一条轻边,则该轻边一定连接了一条轻边的顶点 Top。不妨设 dep[Top[u]]≤dep[Top[v]] ,那么我们可以得到 fa[Top[v]] 属于 u 所在重链。就像求LCA一样,我们把v上移到 fa[Top[v]] ,又归属于情况①,而 v 上移的一段也是一条重链,这段重链所属区间为 [ID[Top[v]],ID[v]] (ID[Top[v]] ≤ ID[v],因为Top[v]的深度一定小于等于v)。
这样答案就变成了两个区间 [ID[Top[v]],ID[v]] 和 [ID[fa[Top[v]]],ID[u]] 。
③ 普通情况
过程越发的像LCA了——我们的目的越发清晰——将u、v移动到同一条重链上。
我们不断的重复将点 x 做下列操作:
移动到 Top[x] -> 线段树区间处理 -> 移动到 fa[x] -> 移动到 Top[x]....
给一个伪代码把:
while(u,v不在同一个重链)
{
保证 Top[u]的深度>Top[v]的深度 //我们固定移动u,所以一定要让u移动后不会离v的重链越来越远
记录答案/修改区间 [ID[Top[u]],ID[u]]
u 移动到 fa[Top[u]]
}
//现在u、v在同一个重链了
转换为问题①
如何判断u、v是否属于同一个重链?还记得 Top吗? 同一个重链上的点的 Top 一定相同啊,所以只需要判断 Top 是否相同就行了。 QwQ
举个例子模拟一下:
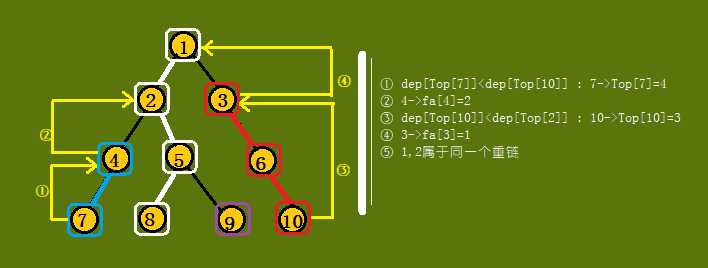
三、一道板板题 +洛谷 3384 树链剖分模板题+
就是两种问题——对子树以及对路径。大家可以看看代码,先熟悉一下……

1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 using namespace std; 7 const int MAXN=int(1e5); 8 int n,t,rt,mod; 9 vector<int> lnk[MAXN+5]; 10 int val[MAXN+5]; 11 int dep[MAXN+5],fa[MAXN+5],heavy[MAXN+5],siz[MAXN+5]; 12 void DFS1(int u,int Fa,int Dep) 13 { 14 dep[u]=Dep;fa[u]=Fa; //更新深度、父节点 15 siz[u]=1; //将u本身计入siz 16 int MAX_siz=0; //最大子树大小 17 for(int i=0;i<lnk[u].size();i++) 18 if(lnk[u][i]!=Fa) //避免重复错误 19 { 20 int v=lnk[u][i]; 21 DFS1(v,u,Dep+1); 22 siz[u]+=siz[v]; //统计大小 23 if(siz[v]>MAX_siz) 24 MAX_siz=siz[v],heavy[u]=v; //求重儿子 25 } 26 } 27 int ID[MAXN+5],fval[MAXN+5],Top[MAXN+5],ID_cnt; 28 void DFS2(int u,int topf) 29 { 30 ID[u]=++ID_cnt;fval[ID_cnt]=val[u]; //ID_cnt 就是当前的DFS序;同时给fval赋值 31 Top[u]=topf; 32 if(!heavy[u]) return; //叶子节点 33 DFS2(heavy[u],topf); 34 for(int i=0;i<lnk[u].size();i++) 35 { 36 int v=lnk[u][i]; 37 if(ID[v]) continue; //避免访问重复 38 DFS2(v,v); //v是另一条重链的起点 39 } 40 } 41 struct TREE{ 42 int l,r,val,siz,lazy; 43 TREE(){} 44 TREE(int fl,int fr){ 45 l=fl,r=fr;siz=r-l+1,lazy=0; 46 } 47 }tree[MAXN*4+5]; 48 //上传更新总和 49 void Update(int x){tree[x].val=((tree[x<<1].val+tree[x<<1|1].val)%mod+mod)%mod;} 50 //下传懒标记 51 void PushDown(int x) 52 { 53 tree[x<<1].val=(tree[x<<1].val+tree[x<<1].siz*tree[x].lazy)%mod; 54 tree[x<<1|1].val=(tree[x<<1|1].val+tree[x<<1|1].siz*tree[x].lazy)%mod; 55 tree[x<<1].lazy=(tree[x<<1].lazy+tree[x].lazy)%mod; 56 tree[x<<1|1].lazy=(tree[x<<1|1].lazy+tree[x].lazy)%mod; 57 tree[x].lazy=0; 58 } 59 //构造线段树 60 void Build(int l,int r,int x) 61 { 62 tree[x]=TREE(l,r); 63 if(l==r) {tree[x].val=fval[l];return;} 64 int mid=(l+r)>>1; 65 Build(l,mid,x<<1); 66 Build(mid+1,r,x<<1|1); 67 Update(x); 68 } 69 //给[L,R]的每个元素加上add 70 void Add(int L,int R,int add,int x) 71 { 72 if(L>tree[x].r || R<tree[x].l) return; 73 if(L<=tree[x].l && tree[x].r<=R) 74 { 75 tree[x].val+=tree[x].siz*add; 76 tree[x].lazy+=add; 77 return; 78 } 79 PushDown(x); 80 Add(L,R,add,x<<1); 81 Add(L,R,add,x<<1|1); 82 Update(x); 83 } 84 //求[L,R]中元素的和 85 int Sum(int x,int L,int R) 86 { 87 if(L>tree[x].r || R<tree[x].l) 88 return 0; 89 if(L<=tree[x].l && tree[x].r<=R) 90 return tree[x].val; 91 PushDown(x); 92 return (Sum(x<<1,L,R)+Sum(x<<1|1,L,R))%mod; 93 } 94 //求路径 u->v 的总和 95 int Road(int u,int v) 96 { 97 int ret=0; 98 while(Top[u]!=Top[v]) 99 { 100 if(dep[Top[u]]<dep[Top[v]]) swap(u,v); //保证Top[u]在Top[v]下 101 ret=(ret+Sum(1,ID[Top[u]],ID[u]))%mod; //更新答案 102 u=fa[Top[u]]; //移动u 103 }//此时u,v应该属于同一条重链了 104 if(dep[u]>dep[v]) swap(u,v); 105 ret=(ret+Sum(1,ID[u],ID[v]))%mod; //同一重链中计算 106 return ret; 107 } 108 //修改路径 u->v 109 void Insert(int u,int v,int add) 110 { 111 while(Top[u]!=Top[v]) 112 { 113 if(dep[Top[u]]<dep[Top[v]]) swap(u,v); 114 Add(ID[Top[u]],ID[u],add,1); //利用线段树修改一段重链 115 u=fa[Top[u]]; 116 } 117 if(dep[u]>dep[v]) swap(u,v); 118 Add(ID[u],ID[v],add,1); //最后一段u->v 119 } 120 int main() 121 { 122 scanf("%d%d%d%d",&n,&t,&rt,&mod); 123 for(int i=1;i<=n;i++) 124 scanf("%d",&val[i]); 125 for(int i=1;i<n;i++) 126 { 127 int u,v;scanf("%d%d",&u,&v); 128 lnk[u].push_back(v);lnk[v].push_back(u); 129 } 130 DFS1(rt,0,1); 131 DFS2(rt,rt); 132 Build(1,n,1); 133 while(t--) 134 { 135 int cmd;scanf("%d",&cmd); 136 int x,y,z; 137 switch(cmd) 138 { 139 case 1: scanf("%d%d%d",&x,&y,&z);Insert(x,y,z%mod);break; 140 case 2: scanf("%d%d",&x,&y);printf("%d ",Road(x,y));break; 141 case 3: scanf("%d%d",&x,&y);Add(ID[x],ID[x]+siz[x]-1,y%mod,1);break; 142 case 4: scanf("%d",&x);printf("%d ",Sum(1,ID[x],ID[x]+siz[x]-1));break; 143 } 144 } 145 return 0; 146 }
The End
Thanks for reading!
- Lucky_Glass
以上是关于模板时间◆模板·II◆ 树链剖分的主要内容,如果未能解决你的问题,请参考以下文章
