静态可持久化线段树（主席树）

Posted 2020-12-24 2020pengxiyue

题目背景

这是个非常经典的主席树入门题——静态区间第K小

数据已经过加强，请使用主席树。同时请注意常数优化

题目描述

如题，给定N个正整数构成的序列，将对于指定的闭区间查询其区间内的第K小值。

输入输出格式

输入格式：

 

第一行包含两个正整数N、M，分别表示序列的长度和查询的个数。

第二行包含N个正整数，表示这个序列各项的数字。

接下来M行每行包含三个整数 l, r, kl,r,k , 表示查询区间 [l, r][l,r] 内的第k小值。

 

输出格式：

 

输出包含k行，每行1个正整数，依次表示每一次查询的结果

 

题解及静态可持久化线段树总结

　　对于求取第k大的问题我们通常运用的是权值线段树来解决，但是，单颗权值线段树只能求解在整个取件中第k大的数，而我们要求解的是区间中第k大的数，自然一颗权值线段树就不能解决了。那么，我们考虑如何用多颗权值线段树来维护一个区间的第k大呢？

　　对于一个区间[l, r]的和我们可以把它看作两个区间[1, l - 1]的和与[1, r -1]的和作差，这说明和的运算满足“区间上的可加性”，但是区间中的第几大满不满足这种“区间上的可加性”呢？

　　证明如下：

　　对于一个数a[i]在区间[1, l -1]中有(k1 - 1)个数比他小（即他排在k1位），在区间[1, r]中有(k2 - 1)个数比他小（即他排在k2位），又因为l - 1 < r，所以在[1, l - 1]区间中的(k1 - 1)个数一定都存在于区间[1, r]中，那么剩余的(k2 - k1)个数一定都存在于[l, r]中，所以满足“区间上的可加性”，证毕。

　　既然，区间第k大满足这种“区间可加性”，那么我们就可以开n颗权值线段树分别维护[1,1], [1,2],……，[1, n]的区间第k大，但是我们如果开n颗线段树的话空间是一定会炸掉的，所以，我们就要通过重复利用空间来使得整个所有的空间尽量的小。

　　就像这样：（示例： 数列（4,1,3,2）查询（区间[1,3]中第2大）

　　圈内中是这个数的sum（权值），圈外是结点下标。

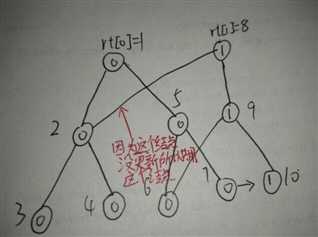
　　如果我们对于每一个插入的数都进行这样的操作的话就会形成这样的一幅图：

 

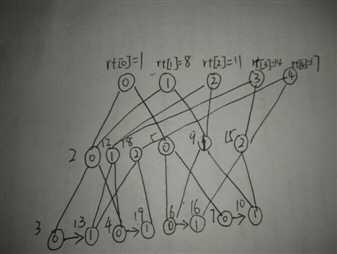
相关操作

　　建树

　　对于一颗主席树，我们要先一颗空树（所有的权值都为0）作为其他树的依靠，这就和普通的建立一颗线段树一样。

 void Build(pointer rt, int l, int r)
        {
            rt->l = l, rt->r = r;
            if(r - l == 0)
            {
                rt->sum = 0;
                return;
            }
            rt->lson = new Node(), rt->rson = new ()Node;
            Build(rt->lson, l , rt->mid()), Build(rt->rson, rt->mid() + 1, r);
            Pushup(rt);
        }

更新（加入其他的点）

　　对于所有的新加入的点只改变这个点到根的路径，路径上，所以我们只要新开一个结点向下递归到叶子结点即可，然后再用点连起来。

 void Updata(pointer prert ,pointer rt, int l, int r, int x, int y)
        {
            rt->l = l, rt->r = r;
            if(r - l == 0)
            {
                rt->sum += y;
                return;
            }
            if(x <= rt->mid())
            {
                rt->lson = new Node();
                Updata(prert->lson, rt->lson, l, rt->mid(), x, y);
                rt->rson = prert->rson;
                Pushup(rt);
            }
            else
            {
                rt->rson = new Node();
                Updata(prert->rson, rt->rson, rt->mid() + 1, r, x, y);
                rt->lson= prert->lson;
                Pushup(rt);
            }
        }

　查询（同权值线段树）

int Query(pointer rtl, pointer rtr, int k)
        {
            if(rtl->r - rtl->l == 0)    return rtl->l;
            int d = rtr->lson->sum - rtl->lson->sum;
            if(d >= k)    return Query(rtl->lson, rtr->lson, k);
            else    return Query(rtl->rson, rtr->rson, k - d);
        }

代码

#include <bits/stdc++.h>
using namespace std;

const int MAX = 200005;

typedef struct Node{
    int l, r, sum;
    Node *lson, *rson;
    Node():l(0), r(0), sum(0), lson(NULL), rson(NULL){}
    int mid(){return (l + r) >> 1;}
    int len(){return r - l;}
}node, *pointer;

class Durable_Segement_Tree{
private:
    void Pushup(pointer rt)
        {
            rt->sum = rt->lson->sum + rt->rson->sum;
        }

public:
    pointer root[MAX];
    int a[MAX], num[MAX];

    void Build(pointer rt, int l, int r)
        {
            rt->l = l, rt->r = r;
            if(r - l == 0)
            {
                rt->sum = 0;
                return;
            }
            rt->lson = new Node(), rt->rson = new ()Node;
            Build(rt->lson, l , rt->mid()), Build(rt->rson, rt->mid() + 1, r);
            Pushup(rt);
        }

    void Updata(pointer prert ,pointer rt, int l, int r, int x, int y)
        {
            rt->l = l, rt->r = r;
            if(r - l == 0)
            {
                rt->sum += y;
                return;
            }
            if(x <= rt->mid())
            {
                rt->lson = new Node();
                Updata(prert->lson, rt->lson, l, rt->mid(), x, y);
                rt->rson = prert->rson;
                Pushup(rt);
            }
            else
            {
                rt->rson = new Node();
                Updata(prert->rson, rt->rson, rt->mid() + 1, r, x, y);
                rt->lson= prert->lson;
                Pushup(rt);
            }
        }

    int Query(pointer rtl, pointer rtr, int k)
        {
            if(rtl->r - rtl->l == 0)    return rtl->l;
            int d = rtr->lson->sum - rtl->lson->sum;
            if(d >= k)    return Query(rtl->lson, rtr->lson, k);
            else    return Query(rtl->rson, rtr->rson, k - d);
        }

};

struct VAL
{
    int val, pos;
}p[MAX];

int ans[MAX];
Durable_Segement_Tree tree;
bool comp1(const VAL & a, const VAL & b)    {return a.val < b.val;}
bool comp2(const VAL & a, const VAL & b)    {return a.pos < b.pos;}
int main()
{
//    freopen("3834.in", "r", stdin);
//    freopen("3834.out", "w", stdout);
    
    memset(tree.num, 0, sizeof(tree.num));
    int n, m, x, y, k;
    int cnt = 0;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++ i)
    {
        scanf("%d", &p[i].val);
        p[i].pos = i;
    }
    tree.root[0] = new Node();
    tree.Build(tree.root[0], 1, n);
    sort(p + 1, p + n+1, comp1);
    for(int i = 1; i <= n; ++ i)
        {
        //    if(p[i].val != p[i - 1].val)    tree.a[p[i].pos] = ++ cnt, ans[cnt] = p[i].val;
            tree.a[p[i].pos] = i;
            tree.num[p[i].pos] ++;
        }
//    sort(p + 1, p + n+1, comp2);
    for(int i = 1; i <= n; ++ i)
    {
        tree.root[i] = new Node();
        tree.Updata(tree.root[i - 1], tree.root[i], 1, n, tree.a[i], tree.num[i]);
    }
    for(int i = 1; i <= m; ++ i)
    {
        scanf("%d%d%d", &x, &y, &k);
        printf("%d
", p[tree.Query(tree.root[x - 1], tree.root[y], k)].val);
    }
}

 

参考文献

http://www.cnblogs.com/zyf0163/p/4749042.html