可持久化

Posted 2021-08-30 Jozky86

文章目录

• 【可持久化值域线段树/主席树】
• • 主席树代码
  • 【二维数点】
  • 例题

【可持久化值域线段树/主席树】

P3834 【模板】可持久化线段树 1（主席树）
查询序列区间第k小，静态在线。给定 n 个整数构成的序列，将对于指定的闭区间查询其区间内的第 k 小值。

类似值域线段树上二分求kth的方法，对于[l,r]区间内部的 kth，若有[1,l-1]和[1,r]2个前缀所对应的2棵值域线段树rt0/rt1，也可以通过：

比较 getSZ(rt1->ls) - getSZ(rt0->ls) 和 当前k 的大小关系

来二分答案。

为了构建所有前缀[1,i]对应的动态开点值域线段树，用可持久化的方式依次将a[1…N]加入值域线段树，每次加入都生成一个新版本即可。空间O(NlogN)，同时拥有 N棵 值域线段树。注意这里主席树支持在线询问，但不支持修改。时间复杂度O(QlogN)。

主席树代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<stack>
#include<cmath>
#include<set>
#include<map>
using namespace std;
#define ll long long
 
typedef pair<int,int>P;
const int INF=0x3f3f3f3f;
const int N=200005;
int a[N],b[N],tot=0;
int rt[N],ls[N*20],rs[N*20],sum[N*20];
 
void build(int &o,int l,int r){
    o=++tot;
    sum[o]=0;
    if(l==r)return ;
    int m=(l+r)>>1;
    build(ls[o],l,m);
    build(rs[o],m+1,r);
}
 
void update(int &o,int l,int r,int pre,int p){
    o=++tot;
    ls[o]=ls[pre];
    rs[o]=rs[pre];
    sum[o]=sum[pre]+1;
    if(l==r)return ;
    int m=(l+r)>>1;
    if(p<=m)update(ls[o],l,m,ls[pre],p);
    else update(rs[o],m+1,r,rs[pre],p);
}
 
int query(int lr,int rr,int l,int r,int k){
    if(l==r)return l;
    int m=(l+r)>>1;
    int cnt=sum[ls[rr]]-sum[ls[lr]];
    if(k<=cnt)return query(ls[lr],ls[rr],l,m,k);
    else return query(rs[lr],rs[rr],m+1,r,k-cnt);
}
 
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        b[i]=a[i];
    }
    sort(a+1,a+1+n);
    int nn=unique(a+1,a+1+n)-(a+1);
    int l,r,k;
    build(rt[0],1,nn);
    for(int i=1;i<=n;i++){
        int x=lower_bound(a+1,a+1+nn,b[i])-a;
        update(rt[i],1,nn,rt[i-1],x);
    }
    while(m--){
        scanf("%d%d%d",&l,&r,&k);
        int ans=query(rt[l-1],rt[r],1,nn,k);
        printf("%d\\n",a[ans]);
    }
}

【二维数点】

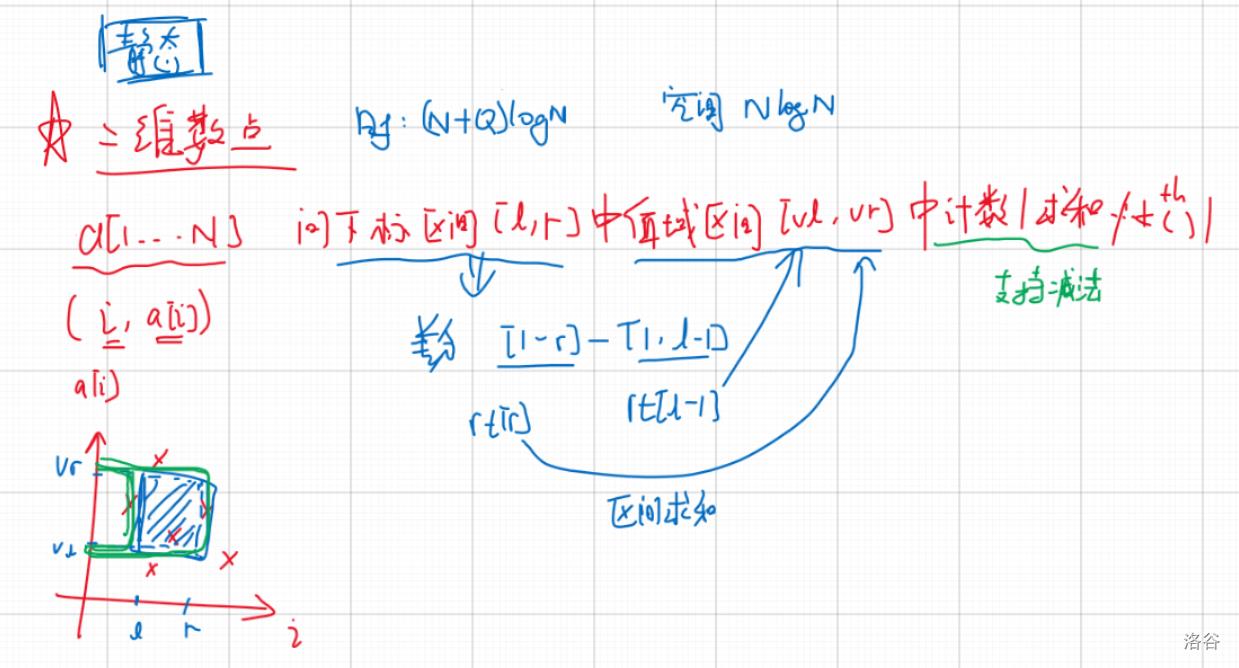
这里的可持久化值域线段树支持对一个下标区间[l,r]中值域区间[vl,vr]内的计数/求和等操作，相当与静态二维数点，复杂度1个log。注意这里不支持动态修改。
二维数点就是将(i,a[i])加入到主席树中，比如查询[l,r]中值域区间[vl,vr]中点的数量，在第r个树中求[vl,vr]d的区间和（因为是值域线段树），在第l-1个树中求[vl,vr]的区间和，就用第r个树(tr[r])减去树(tr[l-1])

#include<bits/stdc++.h>
#define LL long long
#define INF (1<<20)
#define MAXN 100005
#define getSZ(p) (p?p->sz:0)
#define getLSZ(p) (p?getSZ(p->ls):0)
#define getL(p) (p?p->ls:0)
#define getR(p) (p?p->rs:0)
using namespace std;

struct Node{
    int l,r,sz;
    Node *ls, *rs;

    void update(){
        sz = getSZ(ls) + getSZ(rs);
    }

} pool[50*MAXN], *rt[MAXN];

int top = 0;
int N,Q;

Node* copyNode(Node* rt){
    Node *p = pool + (++top);
    *p = *rt;
    return p;
}

Node* newNode(int l, int r){
    Node *p = pool + (++top);
    p->l = l; p->r = r;
    return p;
}

Node* insert(Node* rt, int l, int r, int x){
    Node *p;
    if(rt) p = copyNode(rt);
    else p = newNode(l,r);

    ++p->sz;
    if(p->l==x && p->r==x) return p;

    int mid = (l + r)/2;
    if(x<=mid) p->ls = insert(p->ls, l, mid, x);
    else p->rs = insert(p->rs, mid+1, r, x);

    p->update();
    return p;
}

int query(Node* pL, Node* pR, Node* p0, Node* p1, int k){
    if(pR && pR->l==pR->r) return pR->l;
    if(pL && pL->l==pL->r) return pL->l;

    int k1 = getLSZ(pL) + getLSZ(pR) - getLSZ(p0) - getLSZ(p1);
    if(k1 >= k) return query(getL(pL), getL(pR), getL(p0), getL(p1), k);
    else return query(getR(pL), getR(pR), getR(p0), getR(p1), k - k1);
}

int a[MAXN], c[MAXN];
vector<int> adj[MAXN];
bool vis[MAXN];
int anc[MAXN][21], dep[MAXN];

void dfs(int u, int fa){
    vis[u] = 1;
    rt[u] = insert(rt[fa], 1, N, a[u]);
    for(int j=1;j<=20;j++){
        if(dep[u] <= (1<<j)) break;
        anc[u][j] = anc[anc[u][j-1]][j-1];
    }

    int v;
    for(int k=0;k<adj[u].size();k++){
        v = adj[u][k];
        if(vis[v]) continue;

        dep[v] = dep[u] + 1; anc[v][0] = u;
        dfs(v, u);
    }
}

int lca(int u, int v){
    if(dep[u] < dep[v]) swap(u,v);
    for(int j=20;j>=0;j--){
        if(dep[anc[u][j]] >= dep[v]){
            u = anc[u][j];
        }
    }
    if(u == v) return u;
    for(int j=20;j>=0;j--){
        if(anc[u][j] != anc[v][j]){
            u = anc[u][j];
            v = anc[v][j];
        }
    }
    return anc[u][0];
} 

int main(){

    scanf("%d%d", &N, &Q);
    for(int i=1;i<=N;i++) scanf("%d", &a[i]);

    memcpy(c,a,sizeof(a));
    sort(c+1,c+1+N);
    for(int i=1;i<=N;i++){
        a[i] = lower_bound(c+1,c+1+N,a[i]) - c;
    }

    int u,v;
    for(int i=1;i<N;i++){
        scanf("%d%d", &u, &v);
        adj[u].push_back(v);
        adj[v].push_back(u);
    }

    dep[1] = 1;
    dfs(1,0);

    int k, z, lastans = 0;
    while(Q--){
        scanf("%d%d%d", &u, &v, &k);
        u ^= lastans;
        z = lca(u, v);
        lastans = c[query(rt[u], rt[v], rt[z], rt[anc[z][0]], k)];
        printf("%d\\n", lastans);
    }

    return 0;
}

例题

P2633 Count on a tree
P3567 [POI2014]KUR-Couriers