merge sort

Posted 2020-12-24 guxuanqing

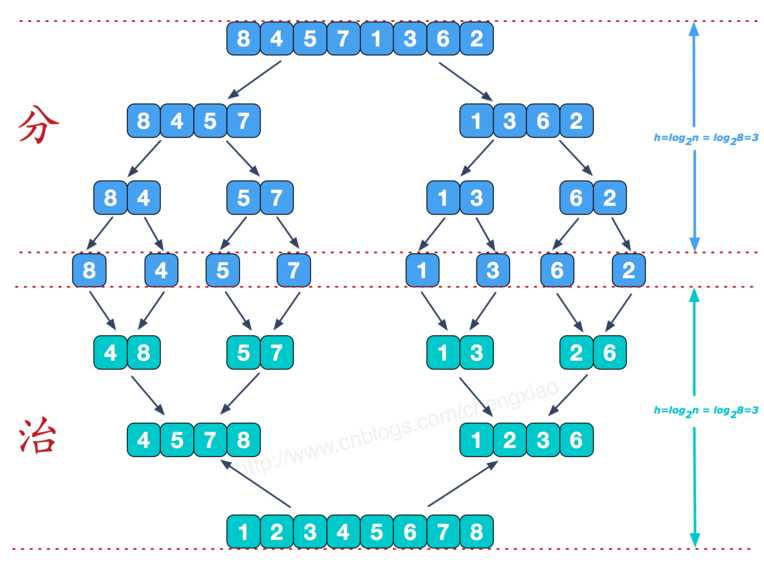
归并排序：归并排序（英语：Merge sort，或mergesort），是创建在归并操作上的一种有效的排序算法，效率为O(n log n)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。

该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

归并排序是稳定排序，它也是一种十分高效的排序

 

 

 

void mergeSort ( int array[], int min, int max)
{
    // prerequisite
    if (min < max)
    {
        // get the middle point
        int mid = ( int )floor((max + min) / 2) ;
        // apply merge sort to both parts of this
        mergeSort(array, min, mid) ;
        mergeSort(array, mid + 1, max) ;
        // and finally merge all that sorted stuff
        merge(array, min, max, mid) ;
    }
}
void merge ( int array[], int min, int max, int mid)
{
    int firstIndex = min ;
    int secondIndex = mid + 1 ;
    int index = min ;
    int tempArray[max] ;
    // if there are still objects in both arrays
    while ((firstIndex <= mid) && (secondIndex <= max))
    {
        if (array[firstIndex] < array[secondIndex])
        {
            tempArray[index] = array[firstIndex] ;
            index ++ ;
            firstIndex ++ ;
        }
        else
        {
            tempArray[index] = array[secondIndex] ;
            index ++ ;
            secondIndex ++ ;
        }
    }
    // terminates the object of the lower array
    while (firstIndex <= mid)
    {
        tempArray[index] = array[firstIndex] ;
        index ++ ;
        firstIndex ++ ;
    }
    // terminates the object of the upper array
    while (secondIndex <= max)
    {
        tempArray[index] = array[secondIndex] ;
        index ++ ;
        secondIndex ++ ;
    }
    // transfer to the initial array
    for ( int i = min ; i < index ; i ++ )
        array[i] = tempArray[i] ;
}

 

总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。