最长上升子序列 (LIS) 详解+例题模板 (全)(转)
Posted zl1991
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最长上升子序列 (LIS) 详解+例题模板 (全)(转)相关的知识,希望对你有一定的参考价值。
1.摘要:
关于LIS部分,本篇博客讲一下LIS的概念定义和理解,以及求LIS的三种方法,分别是O(n^2)的DP,O(nlogn)的二分+贪心法,以及O(nlogn)的树状数组优化的DP,最后附上几道非常经典的LIS的例题及分析。
2.LIS的定义:
最长上升子序列(Longest Increasing Subsequence),简称LIS,也有些情况求的是最长非降序子序列,二者区别就是序列中是否可以有相等的数。假设我们有一个序列 b i,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们也可以从中得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … < iK <= N,但必须按照从前到后的顺序。比如,对于序列(1, 7, 3, 5, 9, 4, 8),我们就会得到一些上升的子序列,如(1, 7, 9), (3, 4, 8), (1, 3, 5, 8)等等,而这些子序列中最长的(如子序列(1, 3, 5, 8) ),它的长度为4,因此该序列的最长上升子序列长度为4。
是不是觉得好抽象~没事我给你解释~
首先需要知道,子串和子序列的概念,我们以字符子串和字符子序列为例,更为形象,也能顺带着理解字符的子串和子序列:
(1)字符子串指的是字符串中连续的n个字符,如abcdefg中,ab,cde,fg等都属于它的字串。
(2)字符子序列指的是字符串中不一定连续但先后顺序一致的n个字符,即可以去掉字符串中的部分字符,但不可改变其前后顺序。如abcdefg中,acdg,bdf属于它的子序列,而bac,dbfg则不是,因为它们与字符串的字符顺序不一致。
知道了这个,数值的子序列就很好明白了,即用数组成的子序列。这样的话,最长上升子序列也很容易明白了,归根结底还是子序列,然后子序列中,按照上升顺序排列的最长的就是我们最长上升子序列了,这样听来是不是就很容易明白啦~
还有一个非常重要的问题:请大家用集合的观点来理解这些概念,子序列、公共子序列以及最长公共子序列都不唯一,但很显然,对于固定的数组,虽然LIS序列不一定唯一,但LIS的长度是唯一的。再拿我们刚刚举的栗子来讲,给出序列 ( 1, 7, 3, 5, 9, 4, 8),易得最长上升子序列长度为4,这是确定的,但序列可以为 ( 1, 3, 5, 8 ), 也可以为 ( 1, 3, 5, 9 )。
3.LIS长度的求解方法:
那么这个到底该怎么求呢?
这里详细介绍一下求LIS的三种方法,分别是O(n^2)的DP,O(nlogn)的二分+贪心法,以及O(nlogn)的树状数组优化的DP。
解法1:动态规划:
我们都知道,动态规划的一个特点就是当前解可以由上一个阶段的解推出, 由此,把我们要求的问题简化成一个更小的子问题。子问题具有相同的求解方式,只不过是规模小了而已。最长上升子序列就符合这一特性。我们要求n个数的最长上升子序列,可以求前n-1个数的最长上升子序列,再跟第n个数进行判断。求前n-1个数的最长上升子序列,可以通过求前n-2个数的最长上升子序列……直到求前1个数的最长上升子序列,此时LIS当然为1。
让我们举个例子:求 2 7 1 5 6 4 3 8 9 的最长上升子序列。我们定义d(i) (i∈[1,n])来表示前i个数以A[i]结尾的最长上升子序列长度。
前1个数 d(1)=1 子序列为2;
前2个数 7前面有2小于7 d(2)=d(1)+1=2 子序列为2 7
前3个数 在1前面没有比1更小的,1自身组成长度为1的子序列 d(3)=1 子序列为1
前4个数 5前面有2小于5 d(4)=d(1)+1=2 子序列为2 5
前5个数 6前面有2 5小于6 d(5)=d(4)+1=3 子序列为2 5 6
前6个数 4前面有2小于4 d(6)=d(1)+1=2 子序列为2 4
前7个数 3前面有2小于3 d(3)=d(1)+1=2 子序列为2 3
前8个数 8前面有2 5 6小于8 d(8)=d(5)+1=4 子序列为2 5 6 8
前9个数 9前面有2 5 6 8小于9 d(9)=d(8)+1=5 子序列为2 5 6 8 9
d(i)=max{d(1),d(2),……,d(i)} 我们可以看出这9个数的LIS为d(9)=5
总结一下,d(i)就是找以A[i]结尾的,在A[i]之前的最长上升子序列+1,当A[i]之前没有比A[i]更小的数时,d(i)=1。所有的d(i)里面最大的那个就是最长上升子序列。其实说的通俗点,就是每次都向前找比它小的数和比它大的数的位置,将第一个比它大的替换掉,这样操作虽然LIS序列的具体数字可能会变,但是很明显LIS长度还是不变的,因为只是把数替换掉了,并没有改变增加或者减少长度。但是我们通过这种方式是无法求出最长上升子序列具体是什么的,这点和最长公共子序列不同。
如果非要求LIS具体序列,阔以参考一下 ZOJ 4028, 即第15届浙江省赛题E题 ------ LIS,题解戳这里~ 。
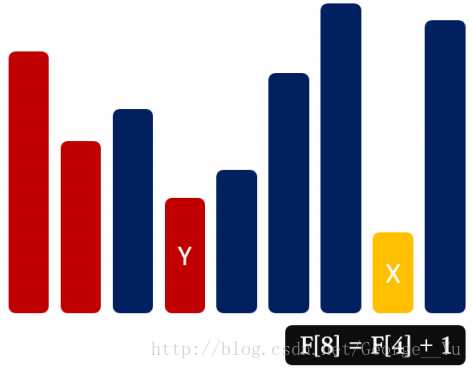
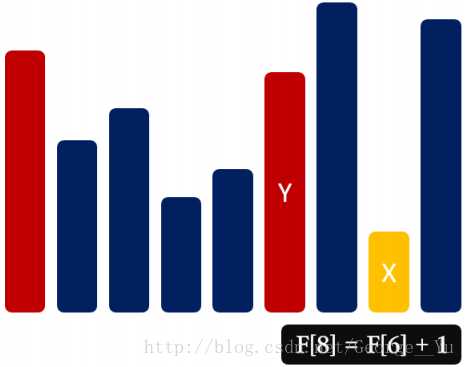
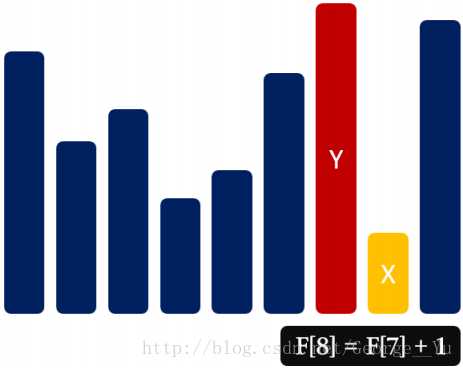
状态设计:F [ i ] 代表以 A [ i ] 结尾的 LIS 的长度
状态转移:F [ i ] = max { F [ j ] + 1 ,F [ i ] } (1 <= j < i,A[ j ] < A[ i ])
边界处理:F [ i ] = 1 (1 <= i <= n)
时间复杂度:O (n^2)
话不多说,show me the code!
代码实现:
#include <iostream> #include <cstdio> #include <algorithm> #include <cstdlib> #include <cstring> #include <cmath> using namespace std; const int maxn = 103, INF = 0x7f7f7f7f; int a[maxn], f[maxn]; int n,ans = -INF; int main() { scanf("%d", &n); for(int i=1; i<=n; i++) { scanf("%d", &a[i]); f[i] = 1; } for(int i=1; i<=n; i++) for(int j=1; j<i; j++) if(a[j] < a[i]) f[i] = max(f[i], f[j]+1); for(int i=1; i<=n; i++) ans = max(ans, f[i]); printf("%d ", ans); return 0; }
这个算法的时间复杂度为〇(n²),并不是最优的算法。在限制条件苛刻的情况下,这种方法行不通。那么怎么办呢!有没有时间复杂度更小的算法呢?说到这里了,当然是有的啦!还有一种时间复杂度为〇(nlogn)的算法,下面就来看看。
解法2:贪心+二分:
思路:
新建一个 low 数组,low [ i ]表示长度为i的LIS结尾元素的最小值。对于一个上升子序列,显然其结尾元素越小,越有利于在后面接其他的元素,也就越可能变得更长。因此,我们只需要维护 low 数组,对于每一个a[ i ],如果a[ i ] > low [当前最长的LIS长度],就把 a [ i ]接到当前最长的LIS后面,即low [++当前最长的LIS长度] = a [ i ]。
那么,怎么维护 low 数组呢?
对于每一个a [ i ],如果a [ i ]能接到 LIS 后面,就接上去;否则,就用 a [ i ] 取更新 low 数组。具体方法是,在low数组中找到第一个大于等于a [ i ]的元素low [ j ],用a [ i ]去更新 low [ j ]。如果从头到尾扫一遍 low 数组的话,时间复杂度仍是O(n^2)。我们注意到 low 数组内部一定是单调不降的,所有我们可以二分 low 数组,找出第一个大于等于a[ i ]的元素。二分一次 low 数组的时间复杂度的O(lgn),所以总的时间复杂度是O(nlogn)。
我们再举一个例子:有以下序列A[ ] = 3 1 2 6 4 5 10 7,求LIS长度。
我们定义一个B[ i ]来储存可能的排序序列,len 为LIS长度。我们依次把A[ i ]有序地放进B[ i ]里。
(为了方便,i的范围就从1~n表示第i个数)
A[1] = 3,把3放进B[1],此时B[1] = 3,此时len = 1,最小末尾是3
A[2] = 1,因为1比3小,所以可以把B[1]中的3替换为1,此时B[1] = 1,此时len = 1,最小末尾是1
A[3] = 2,2大于1,就把2放进B[2] = 2,此时B[ ]={1,2},len = 2
同理,A[4]=6,把6放进B[3] = 6,B[ ]={1,2,6},len = 3
A[5]=4,4在2和6之间,比6小,可以把B[3]替换为4,B[ ] = {1,2,4},len = 3
A[6] = 5,B[4] = 5,B[ ] = {1,2,4,5},len = 4
A[7] = 10,B[5] = 10,B[ ] = {1,2,4,5,10},len = 5
A[8] = 7,7在5和10之间,比10小,可以把B[5]替换为7,B[ ] = {1,2,4,5,7},len = 5
最终我们得出LIS长度为5,但是,但是!!!B[ ] 中的序列并不一定是正确的最长上升子序列。在这个例子中,我们得到的1 2 4 5 7 恰好是正确的最长上升子序列,下面我们再举一个例子:有以下序列A[ ] = 1 4 7 2 5 9 10 3,求LIS长度。
A[1] = 1,把1放进B[1],此时B[1] = 1,B[ ] = {1},len = 1
A[2] = 4,把4放进B[2],此时B[2] = 4,B[ ] = {1,4},len = 2
A[3] = 7,把7放进B[3],此时B[3] = 7,B[ ] = {1,4,7},len = 3
A[4] = 2,因为2比4小,所以把B[2]中的4替换为2,此时B[ ] = {1,2,7},len = 3
A[5] = 5,因为5比7小,所以把B[3]中的7替换为5,此时B[ ] = {1,2,5},len = 3
A[6] = 9,把9放进B[4],此时B[4] = 9,B[ ] = {1,2,5,9},len = 4
A[7] = 10,把10放进B[5],此时B[5] = 10,B[ ] = {1,2,5,9,10},len = 5
A[8] = 3,因为3比5小,所以把B[3]中的5替换为3,此时B[ ] = {1,2,3,9,10},len = 5
最终我们得出LIS长度为5。但是,但是!!这里的1 2 3 9 10很明显并不是正确的最长上升子序列。因此,B序列并不一定表示最长上升子序列,它只表示相应最长子序列长度的排好序的最小序列。这有什么用呢?我们最后一步3替换5并没有增加最长子序列的长度,而这一步的意义,在于记录最小序列,代表了一种“最可能性”,只是此种算法为计算LIS而进行的一种替换。假如后面还有两个数据12和15,那么B[ ]将继续更新。
因为在B中插入的数据是有序的,不需要移动,只需要替换,所以可以用二分查找插入的位置,那么插入n个数的时间复杂度为〇(logn),这样我们会把这个求LIS长度的算法复杂度降为了〇(nlogn)。话不多说了,show me the code!
代码实现:
#include <cmath> #include <cstdio> #include <cstdlib> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int maxn =300003, INF = 0x7f7f7f7f; int low[maxn], a[maxn]; int n, ans; int binary_search(int *a, int R, int x) //二分查找,返回a数组中第一个>=x的位置 { int L = 1, mid; while(L <= R) { mid = (L+R) >> 1; if(a[mid] <= x) L = mid + 1; else R = mid - 1; } return L; } int main() { scanf("%d", &n); for(int i=1; i<=n; i++) { scanf("%d", &a[i]); low[i] = INF; //由于low中存的是最小值,所以low初始化为INF } low[1] = a[1]; ans = 1; //初始时LIS长度为1 for(int i=2; i<=n; i++) { if(a[i] > low[ans]) //若a[i]>=low[ans],直接把a[i]接到后面 low[++ans] = a[i]; else //否则,找到low中第一个>=a[i]的位置low[j],用a[i]更新low[j] low[binary_search(low, ans, a[i])] = a[i]; } printf("%d ", ans); //输出答案 return 0; }
这其中用到了二分查找第一个大于等于的,其实C++里面的有一个函数可用代替二分,那就是 —— low_bound( )函数。
lower_bound( )函数:
下面是使用lower_bound优化最长上升子序列。由于长度相同的上升子序列只需要保存结尾最小的那个,而长度递增时,结尾数字的大小也是递增的。最长上升子序列就是找出比他大的第一个数。前面的数都比他小,所以他和这个数的长度相同。然后由于他比较然后小,更新找到的那个值。
#include<stdio.h> #include<string.h> #include<algorithm> using namespace std; int num[10]={3,6,3,2,4,6,7,5,4,3}; const int INF=0x3f3f3f3f; int l=10, g[100], d[100]; int main() { fill(g, g+l, INF); int max_=-1; for(int i=0; i<l; i++) { int j = lower_bound(g, g+l, num[i]) - g; d[i] = j+1; if(max_<d[i]) max_=d[i]; g[j] = num[i]; } printf("%d ", max_); return 0; } 这个算法其实已经不是DP了,有点像贪心。至于复杂度降低其实是因为这个算法里面用到了二分搜索。 本来有N个数要处理是O(n),每次计算要查找N次还是O(n),一共就是O(n^2); 现在搜索换成了O(logn)的二分搜索,总的复杂度就变为O(nlogn)了。 这里主要注意一下lower_bound函数的应用,注意减去的g是地址。 地址 - 地址 = 下标。
解法3:树状数组维护:
我们再来回顾O(n^2)DP的状态转移方程:F [ i ] = max { F [ j ] + 1 ,F [ i ] } (1 <= j < i,A[ j ] < A[ i ])
我们在递推F数组的时候,每次都要把F数组扫一遍求F[ j ]的最大值,时间开销比较大。我们可以借助数据结构来优化这个过程。用树状数组来维护F数组(据说分块也是可以的,但是分块是O(n*sqrt(n))的时间复杂度,不如树状数组跑得快),首先把A数组从小到大排序,同时把A[ i ]在排序之前的序号记录下来。然后从小到大枚举A[ i ],每次用编号小于等于A[ i ]编号的元素的LIS长度+1来更新答案,同时把编号大于等于A[ i ]编号元素的LIS长度+1。因为A数组已经是有序的,所以可以直接更新。有点绕,具体看代码。
还有一点需要注意:树状数组求LIS不去重的话就变成了最长不下降子序列了。
#include <iostream> #include <cstdio> #include <algorithm> #include <cstdlib> #include <cstring> #include <cmath> using namespace std; const int maxn =103,INF=0x7f7f7f7f; struct Node{ int val,num; }z[maxn]; int T[maxn]; int n; bool cmp(Node a,Node b) { return a.val==b.val?a.num<b.num:a.val<b.val; } void modify(int x,int y)//把val[x]替换为val[x]和y中较大的数 { for(;x<=n;x+=x&(-x)) T[x]=max(T[x],y); } int query(int x)//返回val[1]~val[x]中的最大值 { int res=-INF; for(;x;x-=x&(-x)) res=max(res,T[x]); return res; } int main() { int ans=0; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&z[i].val); z[i].num=i;//记住val[i]的编号,有点类似于离散化的处理,但没有去重 } sort(z+1,z+n+1,cmp);//以权值为第一关键字从小到大排序 for(int i=1;i<=n;i++)//按权值从小到大枚举 { int maxx=query(z[i].num);//查询编号小于等于num[i]的LIS最大长度 modify(z[i].num,++maxx);//把长度+1,再去更新前面的LIS长度 ans=max(ans,maxx);//更新答案 } printf("%d ",ans); return 0; }
4.经典例题模板:
例1:Super Jumping! Jumping! Jumping!
Description
Nowadays, a kind of chess game called “Super Jumping! Jumping! Jumping!” is very popular in HDU. Maybe you are a good boy, and know little about this game, so I introduce it to you now.
The game can be played by two or more than two players. It consists of a chessboard(棋盘)and some chessmen(棋子), and all chessmen are marked by a positive integer or “start” or “end”. The player starts from start-point and must jumps into end-point finally. In the course of jumping, the player will visit the chessmen in the path, but everyone must jumps from one chessman to another absolutely bigger (you can assume start-point is a minimum and end-point is a maximum.). And all players cannot go backwards. One jumping can go from a chessman to next, also can go across many chessmen, and even you can straightly get to end-point from start-point. Of course you get zero point in this situation. A player is a winner if and only if he can get a bigger score according to his jumping solution. Note that your score comes from the sum of value on the chessmen in you jumping path.
Your task is to output the maximum value according to the given chessmen list.
Input
Input contains multiple test cases. Each test case is described in a line as follow:
N value_1 value_2 …value_N
It is guarantied that N is not more than 1000 and all value_i are in the range of 32-int.
A test case starting with 0 terminates the input and this test case is not to be processed.
Output
For each case, print the maximum according to rules, and one line one case.
Sample Input
3 1 3 2
4 1 2 3 4
4 3 3 2 1
0
Sample Output
4
10
3
思路:
题意是有N个数字构成的序列,求最大递增子段和,即递增子序列和的最大值,思路就是定义dp[i],表示以a[i]结尾的最大递增子段和,双重for循环,每次求出以a[i]结尾的最大递增子段和。
代码:
#include<math.h> #include<iostream> #include<stdio.h> #include<stdlib.h> #include<string.h> #include<algorithm> #include<queue> #define INF 0x3f3f3f3f using namespace std; int main() { int a[1005],dp[1005],n,i,j,max1; while(scanf("%d",&n)&&n){ max1=0; memset(dp,0,sizeof(dp)); for(i=0;i<=n-1;i++) scanf("%d",&a[i]); dp[0]=a[0]; for(i=1;i<=n-1;i++){ for(j=0;j<=i-1;j++){ if(a[i]>a[j]) dp[i]=max(dp[j]+a[i],dp[i]); } dp[i]=max(dp[i],a[i]); } max1=dp[0]; for(i=0;i<=n-1;i++) max1=max(dp[i],max1); printf("%d ",max1); } return 0; }
例2:FatMouse‘s Speed
Description
FatMouse believes that the fatter a mouse is, the faster it runs. To disprove this, you want to take the data on a collection of mice and put as large a subset of this data as possible into a sequence so that the weights are increasing, but the speeds are decreasing.
Input
Input contains data for a bunch of mice, one mouse per line, terminated by end of file.
The data for a particular mouse will consist of a pair of integers: the first representing its size in grams and the second representing its speed in centimeters per second. Both integers are between 1 and 10000. The data in each test case will contain information for at most 1000 mice.
Two mice may have the same weight, the same speed, or even the same weight and speed.
Output
Your program should output a sequence of lines of data; the first line should contain a number n; the remaining n lines should each contain a single positive integer (each one representing a mouse). If these n integers are m[1], m[2],..., m[n] then it must be the case that W[m[1]] < W[m[2]] < ... < W[m[n]] and S[m[1]] > S[m[2]] > ... > S[m[n]] . In order for the answer to be correct, n should be as large as possible. All inequalities are strict: weights must be strictly increasing, and speeds must be strictly decreasing. There may be many correct outputs for a given input, your program only needs to find one.
Sample Input
6008 1300
6000 2100
500 2000
1000 4000
1100 3000
6000 2000
8000 1400
6000 1200
2000 1900
Sample Output
4
4
5
9
8
思路:
题意是:给你许多组数据,没组两个数,一个代表老鼠的重量,一个代表老鼠的速度,为了证明老鼠越重速度越慢,让你取出几组数据证明,问最多能取出几组。体重要严格递增,速度严格递减,有些思维含量。
代码:
#include<math.h> #include<iostream> #include<stdio.h> #include<stdlib.h> #include<string.h> #include<algorithm> #include<queue> #define INF 0x3f3f3f3f using namespace std; struct A{ int w; int s; int xb; }a[1010]; struct U{ int num; int xb; }dp[1010]; bool cmp(struct A a,struct A b){ if(a.w==b.w) return a.s>b.s; else return a.w<b.w; } int main() { int b[1010],i,j,k,n=0,max1=0; while(scanf("%d%d",&a[n].w,&a[n].s)!=EOF){ ++n; a[n-1].xb=n; } sort(a,a+n,cmp); for(i=0;i<=n-1;i++){ dp[i].num=1; dp[i].xb=0; } for(i=1;i<=n-1;i++){ for(j=0;j<=i-1;j++){ if(a[i].w>a[j].w&&a[i].s<a[j].s&&dp[i].num<dp[j].num+1){ dp[i].num=dp[j].num+1; dp[i].xb=j; } } if(dp[i].num>max1) { max1=dp[i].num; k=i; } } for(i=1;i<=max1;i++) { b[i]=k; k=dp[k].xb; } printf("%d ",max1); for(i=max1;i>=1;i--) printf("%d ",a[b[i]].xb); return 0; }
例3:最少拦截系统
Decription
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统.但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能超过前一发的高度.某天,雷达捕捉到敌国的导弹来袭.由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹.
怎么办呢?多搞几套系统呗!你说说倒蛮容易,成本呢?成本是个大问题啊.所以俺就到这里来求救了,请帮助计算一下最少需要多少套拦截系统.
Input
输入若干组数据.每组数据包括:导弹总个数(正整数),导弹依此飞来的高度(雷达给出的高度数据是不大于30000的正整数,用空格分隔)
Output
对应每组数据输出拦截所有导弹最少要配备多少套这种导弹拦截系统.
Sample Input
8 389 207 155 300 299 170 158 65
Sample Output
2
思路:
这题是一个贪心+LIS,用dp数组存储已经部署好的防御系统能打的最大高度,每来一个新的导弹,判断之前已经部署好的防御系统能否打下当前导弹,如果能的话就选那个最垃圾的防御系统来攻击导弹,如果之前已经部署的最厉害的防御系统也打不下来的话,那么就新部署一个拦截系统来拦截当前导弹。
代码:
#include<cmath> #include<deque> #include<stdio.h> #include<stdlib.h> #include<string.h> #include<iostream> #include<algorithm> #define INS 0x3f3f3f3f #define eps 1e-10 using namespace std; int a[10001],dp[10001]; int main() { int n,i,j,k,z,min1; while(scanf("%d",&n)!=EOF) { for(i=0; i<=n-1; i++) scanf("%d",&a[i]); memset(dp,0,sizeof(dp)); k=1; dp[0]=a[0]; for(i=1; i<=n-1; i++) { z=-1; min1=0x3f3f3f3f; for(j=0; j<=k-1; j++) if(dp[j]<min1&&a[i]<=dp[j]) { z=j; min1=dp[j]; } if(z==-1) dp[k++]=a[i]; else dp[z]=a[i]; } printf("%d ",k); } return 0; }
例4:Bridging signals
Description
‘Oh no, they‘ve done it again‘, cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place. At this late stage of the process, it is too
expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without rossing each other, is imminent. Bearing in mind that there may be housands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?
Figure 1. To the left: The two blocks‘ ports and their signal mapping (4,2,6,3,1,5). To the right: At most three signals may be routed on the silicon surface without crossing each other. The dashed signals must be bridged.
A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number pecifies which port on the right side should be connected to the i:th port on the left side.
Two signals cross if and only if the straight lines connecting the two ports of each pair do.
Input
On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p<40000, the number of ports on the two functional blocks. Then follow p lines, describing the signal mapping: On the i:th line is the port number of the block on the right side which should be connected to the i:th port of the block on the left side.
Output
For each test scenario, output one line containing the maximum number of signals which may be routed on the silicon surface without crossing each other.
Sample Input
4 6 4 2 6 3 1 5 10 2 3 4 5 6 7 8 9 10 1 8 8 7 6 5 4 3 2 1 9 5 8 9 2 3 1 7 4 6
Sample Output
3 9 1 4
思路:
本题为模板题,但需注意不能用普通做法,需要用二分优化,否则会T的。
代码:
#include<math.h> #include<iostream> #include<stdio.h> #include<stdlib.h> #include<string.h> #include<algorithm> #include<queue> using namespace std; int a[40001],dp[40001]; int main() { int T,n,i,len,pos; scanf("%d",&T); while(T--) { scanf("%d",&n); for(i=1; i<=n; i++) scanf("%d",&a[i]); memset(dp,0,sizeof(dp)); len=1;dp[1]=a[1]; for(i=2; i<=n; i++) { if(a[i]<=dp[len]) { pos=lower_bound(dp,dp+len,a[i])-dp; dp[pos]=a[i]; } else { len++; dp[len]=a[i]; } } printf("%d ",len); } return 0; }
注意:
一般来说,为防止T,都会用二分法来找,最为简便的就是通过lower_bound( )函数来进行查找,最常用模板请参考例题,尤其例4。.
5.相关知识:( 建议放在一起比较区分 )
1)最长公共子序列(LCS)戳这里 ~
2)最长回文子串 and 最长回文子序列 (LPS) 戳这里 ~
————————————————
版权声明:本文为CSDN博主「lxt_Lucia」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/lxt_Lucia/article/details/81206439
以上是关于最长上升子序列 (LIS) 详解+例题模板 (全)(转)的主要内容,如果未能解决你的问题,请参考以下文章