Algorithms - Data Structure - Binary Search Tree - 数据结构之二叉搜索树

Posted 2020-12-23 zzyzz

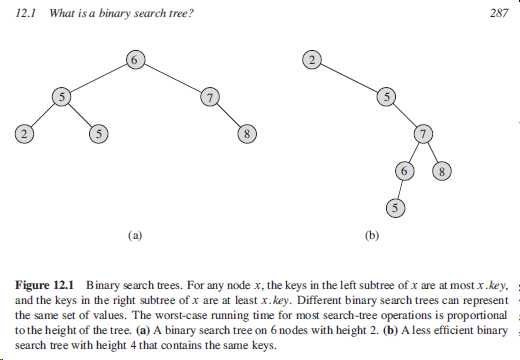
概念
    Binary Search Tree二叉搜索树的性质: 设x是binarysearchtree中的一个节点。
        如果y是x左子树中的一个节点, 那么y.key<=x.key
        如果y是x右子树中的一个节点,那么y.key>=x.key
  

         

Python Programming

# taking the Linked List as the date elements to implement a Binary Search Tree:
# left, right, parent

class tree_element():    #E: [key, left, right, [parent]], the structure of tree element
    def __init__(self, E):
        self.root = E[0]
        self.key = E[0]
        self.left = E[1]
        self.right = E[2]
        self.p = E[3]


class binary_search_tree(list):     #[key, left, right, [parent]]
    # output:  [[2, ‘NIL‘, ‘NIL‘, 4], ‘||‘,
    #           [4, [2, ‘NIL‘, ‘NIL‘, 4], [5, ‘NIL‘, ‘NIL‘, 4], 6], ‘||‘,
    #           [5, ‘NIL‘, ‘NIL‘, 4], ‘||‘,
    #           [6, [4, [2, ‘NIL‘, ‘NIL‘, 4], [5, ‘NIL‘, ‘NIL‘, 4], 6], [7, ‘NIL‘, [8, ‘NIL‘, ‘NIL‘, 7], 6], ‘NIL‘], ‘||‘,
    #           [7, ‘NIL‘, [8, ‘NIL‘, ‘NIL‘, 7], 6], ‘||‘,
    #           [8, ‘NIL‘, ‘NIL‘, 7], ‘||‘]

    def __init__(self, keys, parent, left, right, root):
        # Linked list data structure element
            # self.keys = [2,4,5,6,7,8]
            # self.parent = [4,6,4,‘NIL‘,6,7]
            # self.left = [‘NIL‘,2,‘NIL‘,4,‘NIL‘, ‘NIL‘]
            # self.right = [‘NIL‘,5,‘NIL‘,7,8,‘NIL‘]
            # self.root = 6
        self.keys = keys
        self.parent = parent
        self.left = left
        self.right =right
        self.root = root

    def produce_left(self, key):   # produce x.key‘s left child obj
        ind = self.keys.index(key)
        if self.left[ind] == ‘NIL‘:
            return ‘NIL‘
        else:
            El = []
            El.append(self.left[ind])
            El.append(self.produce_left(self, self.left[ind]))
            El.append(self.produce_right(self, self.left[ind]))
            El.append(self.produce_parent(self, self.left[ind]))
            return tree_element(El)

    def produce_right(self,key):     # produce x.key’s right child obj
        ind = self.keys.index(key)
        if self.right[ind] == ‘NIL‘:
            return ‘NIL‘
        else:
            Er = []
            Er.append(self.right[ind])
            Er.append(self.produce_left(self, self.right[ind]))
            Er.append(self.produce_right(self, self.right[ind]))
            Er.append(self.produce_parent(self, self.right[ind]))
            return tree_element(Er)

    def produce_parent(self,key):    # produce x.key‘s parent obj
        # parent‘ is a bigger tree than the current tree point.
        # a bigger tree contains all the smaller trees
        # hence, we should avoid recursive implementation in produce_parent
        ind = self.keys.index(key)
        if self.parent[ind] == ‘NIL‘:
            return ‘NIL‘
        else:
            # 为避免无限递归, parent 属性不能使用加入 obj 的结构, 这里把parent 的key值加入到 element 结构中
            return self.parent[ind]

    def __new__(self, *args, **kwargs):   # BSD 的是一个 list, 其中包含了树的节点对象, 即其属性(key, parent, left, right)
                                          # 注: 元素属性可以是另一个节点对象
        keys, parent, left, right, root = args
        self.__init__(self,keys, parent, left, right, root)
        obj = super(binary_search_tree, self).__new__(self))
        for i in range(len(self.keys)):
            E = []
            # add key value
            E.append(self.keys[i])
            # add left obj
            print(self.keys[i])
            left = self.produce_left(self, self.keys[i])
            if left == ‘NIL‘:
                E.append(left)
            else:
                E.append(self.produce_left(self, self.keys[i]))
            # add right obj
            right = self.produce_right(self, self.keys[i])
            if right == ‘NIL‘:
                E.append(right)
            else:
                E.append(self.produce_right(self, self.keys[i]))
            # add right obj
                # Note, we can treat ‘parent‘ is a bigger tree than the current tree point
            parent = self.produce_parent(self,self.keys[i])
            if parent == ‘NIL‘:
                E.append(parent)
            else:
                E.append(self.produce_parent(self,self.keys[i]))
            obj.append(tree_element(E))
        return obj

if __name__ == ‘__main__‘:
    keys = [2,4,5,6,7,8]
    parent = [4,6,4,‘NIL‘,6,7]
    left = [‘NIL‘,2,‘NIL‘,4,‘NIL‘, ‘NIL‘]
    right = [‘NIL‘,5,‘NIL‘,7,8,‘NIL‘]
    root = 6

    T = binary_search_tree(keys,parent,left,right,root)

    print(‘BSD : ‘, T, T.root)
    print(‘BSD element :‘)
    for item in T:
        print(‘obj‘, item)
        print(‘Key, Left, Right, Parent : ‘, item.key, item.left, item.right, item.p)

结果打印:

# 根为 6 的 BSD 结构
BSD :  [<__main__.tree_element object at 0x0000000002997C50>, 
        <__main__.tree_element object at 0x0000000002997D68>, 
        <__main__.tree_element object at 0x0000000002997C88>, 
        <__main__.tree_element object at 0x0000000002997F98>, 
        <__main__.tree_element object at 0x0000000002997CF8>, 
        <__main__.tree_element object at 0x0000000002997DA0>] 6

# BSD 每一个结点包含属性: Key, Left, Right, Paren
BSD element :

# 2 这个节点的属性
obj <__main__.tree_element object at 0x0000000002997C50>
Key, Left, Right, Parent :  2 NIL NIL 4

# 节点 4 是节点 2 的 parent,  4 的 left child 节点是节点2的结构. right child 是节点5的结构.
obj <__main__.tree_element object at 0x0000000002997D68>
Key, Left, Right, Parent :  4 <__main__.tree_element object at 0x0000000002997C18> <__main__.tree_element object at 0x0000000002997D30> 6
obj <__main__.tree_element object at 0x0000000002997C88>
Key, Left, Right, Parent :  5 NIL NIL 4
obj <__main__.tree_element object at 0x0000000002997F98>
Key, Left, Right, Parent :  6 <__main__.tree_element object at 0x0000000002997E10> <__main__.tree_element object at 0x0000000002997F28> NIL
obj <__main__.tree_element object at 0x0000000002997CF8>
Key, Left, Right, Parent :  7 NIL <__main__.tree_element object at 0x0000000002997E80> 6
obj <__main__.tree_element object at 0x0000000002997DA0>
Key, Left, Right, Parent :  8 NIL NIL 7

 

Reference

　　1. Introduction to Algorithms