Algorithms - Data Structure - Perfect Hashing - 完全散列

Posted 2021-02-18 zzyzz

相关概念
    散列表 hashtable 是一种实现字典操作的有效数据结构.
    在散列表中,不是直接把关键字作为数组的下标,而是根据关键字计算出相应的下标.
    
    散列函数 hashfunction‘h‘
        除法散列法
        通过取k除以m的余数，将关键k映射到m个slot中的某一个上.即散列函数为:h(k)=kmodm
        比如：散列表的大小m=12,关键字k=100,则h(k)=100mod12=4,放到slot4中.
        由于只需做一次除法,所以除法散列法速度非常快.
        当选择除法散列法的时候,要避免选择m的某些值。例如,m不应为2的幂.因为如果m=2的p次幂.
        则h(k)=就是k的p个最低位数字.
        一个不太接近2的整数次幂的素数,常常是m的一个较好的选择.例如,假定我们要分配一个张散列表用链接
        法解决冲突，表中大约要存放n=2000个字符串,其中每个字符串有8位.如果我们不介意一次不成功的查找
        需要平均检查3个元素,这样分配散列表的大小为701.因为701是一个接近2000/3但是又不接近2的任何次幂的素数.
        
        乘法散列法
        乘法散列法包含两个步骤:第一：用关键字k乘上常数A（0<A<1），并提取kA的小数部分.
        第二步,用m乘以这个值,再向下取整:h(k)=int(m(KAmod1))
        乘法散列的一个优点是对m的选择不是特别关键,一般选m为2个某个次幂.m=2的p次幂.
        
    开放寻址 openaddressing
    开放寻址openaddressing中,所有元素都存放在散列表里.
    每个表项或包含动态集合的一个元素,或包含NIL.当查找某个元素的时候,要系统的检查所有表项,直到找到所需的元素或最终找不到该元素.
    
    有三种技术常用来计算开放寻址法中的probesequence探查序列:线性探查,二次探查和双重探查.
        线性探查 linearprobing: 散列函数:h(k,i)=(h‘(k)+i)modm
        二次探查 quadraticprobing:散列函数：h(k,i)=(h‘(k)+c1i+c2i*i)modm
        双重散列 doublehashing:是用于开放寻址的最好方法,因为它所产生的排列具有随机选择排列的许多特性.
        
        散列函数：h(k,i)=(h1(k)+i*h2(k)modm
        为了能查找整个散列表,值h2(k)必须要与表的大小m互素.一种简单的方法确保这个条件成立,就是取m为2的幂.
        并设计一个总产生奇数的h2.另一个方法是：取m为素数,并设计一个总是返回较m小的正整数的函数h2.
        例如:  h1(k) = k mod m,  h2(k) = 1 + (k mod m‘) , 其中 m‘ 略小于 m, 比如 m‘ = m-1

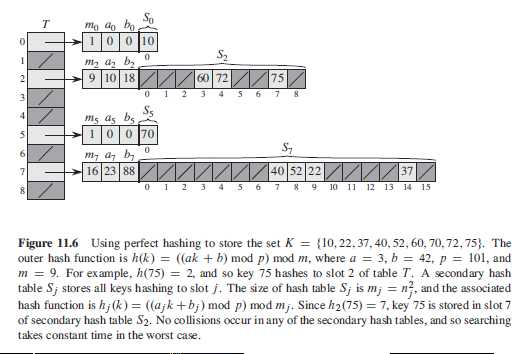
Python program
    Perfect hashing 
        Using perfect hashing to store K=[10,22,37,40,52,60,70,72,75]
        注: 下图中所示元素 40 的位置是不对的. 最后 T 为:

                 T = [[1,0,0,10], ‘NIL‘, [9,10,18,‘NIL‘,‘NIL‘,‘NIL‘,60,72,‘NIL‘,‘NIL‘,75,‘NIL‘], 
                       ‘NIL‘, ‘NIL‘, [1,0,0,70], ‘NIL‘, [16,23,88,‘NIL‘,‘NIL‘,‘NIL‘,‘NIL‘,‘NIL‘,‘NIL‘,
                                                         40,52,22,‘NIL‘,‘NIL‘,‘NIL‘,‘NIL‘,32,‘NIL‘], ‘NIL‘]

           

def produce_t(T0):
    import copy
    T = copy.deepcopy(T0)
    for i in range(len(T)):
        if T[i] != ‘NIL‘:
            T[i] = T[i] + [‘NIL‘ for x in range(T[i][0])]
    return T

def h(k, m=9, a=3, b=42, p=101,):   # h function
    # a = 3
    # b = 42
    # p = 101
    # m = 9
    return ((a*k + b) % p)%m


def perfect_hash(T, k):
    h1 = h(k)
    h2 = h(k,T[h1][0],T[h1][1],T[h1][2])
    T[h1][h2+3] = k
    print(‘  h1 and h2 : ‘, h1,h2)


if __name__ == ‘__main__‘:
    #m = 9

    K = [10, 22, 37, 40, 52, 60, 70, 72, 75]
    # T = [[1,0,0,10], ‘NIL‘, [9,10,18,‘NIL‘,‘NIL‘,‘NIL‘,60,72,‘NIL‘,‘NIL‘,75,‘NIL‘], 
    #      ‘NIL‘, ‘NIL‘, [1,0,0,70], ‘NIL‘, [16,23,88,‘NIL‘,‘NIL‘,‘NIL‘,‘NIL‘,‘NIL‘,‘NIL‘,
    #                                        40,52,22,‘NIL‘,‘NIL‘,‘NIL‘,‘NIL‘,32,‘NIL‘], ‘NIL‘]

    T0 = [[1, 0, 0], ‘NIL‘, [9, 10, 18], ‘NIL‘, ‘NIL‘, [1, 0, 0], ‘NIL‘, [16, 23, 88], ‘NIL‘]
 
    print(‘Initializing T‘)
    T = produce_t(T0)
    #print(T0)
    print(‘T: ‘, T)

    print(‘example of the element 75‘)
    print(‘h result of 75‘)
    print(h(75))
    print(‘Hashing of 75‘)
    perfect_hash(T, 75)
    print(‘T: ‘, T)

    print(‘Hashing of list K‘)
    for i in K:
        print(‘Hashing of : ‘, i)
        perfect_hash(T,i)
    print(‘T: ‘, T)


结果打印:
Initializing T
T:  [[1, 0, 0, ‘NIL‘], ‘NIL‘, [9, 10, 18, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘], 
      ‘NIL‘, ‘NIL‘, [1, 0, 0, ‘NIL‘], ‘NIL‘, 
     [16, 23, 88, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘], ‘NIL‘]

example of the element 75
h result of 75
2
Hashing of 75
  h1 and h2 :  2 7
T:  [[1, 0, 0, ‘NIL‘], ‘NIL‘, [9, 10, 18, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, 75, ‘NIL‘], 
      ‘NIL‘, ‘NIL‘, [1, 0, 0, ‘NIL‘], ‘NIL‘, 
     [16, 23, 88, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘], ‘NIL‘]

Hashing of list K
Hashing of :  10
  h1 and h2 :  0 0
Hashing of :  22
  h1 and h2 :  7 9
Hashing of :  37
  h1 and h2 :  7 14
Hashing of :  40
  h1 and h2 :  7 3
Hashing of :  52
  h1 and h2 :  7 8
Hashing of :  60
  h1 and h2 :  2 3
Hashing of :  70
  h1 and h2 :  5 0
Hashing of :  72
  h1 and h2 :  2 4
Hashing of :  75
  h1 and h2 :  2 7
T:  [[1, 0, 0, 10], ‘NIL‘, [9, 10, 18, ‘NIL‘, ‘NIL‘, ‘NIL‘, 60, 72, ‘NIL‘, ‘NIL‘, 75, ‘NIL‘], 
      ‘NIL‘, ‘NIL‘, [1, 0, 0, 70], ‘NIL‘, 
     [16, 23, 88, ‘NIL‘, ‘NIL‘, ‘NIL‘, 40, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, 52, 22, ‘NIL‘, ‘NIL‘, ‘NIL‘, ‘NIL‘, 37, ‘NIL‘], ‘NIL‘]

 

Reference 

    1. Introduction to algorithms