厄拉多筛法 && 204. 计数质数

Posted 2020-12-21 anullvalue

1.1 定义

厄拉多塞到底是怎样筛选素数的呢？他造了一张1到50的素数表，首先写上1到50的所有自然数，然后先划去1，把2留下，再划去其他所有2的倍数，把3留下。再划去其他所有3的倍数，把5留下。又划去其他所有5的倍数……依此类推，可以得到50以内的所有素数。这就是著名的“厄拉多塞筛法”。

 

1.2计数质数

统计所有小于非负整数 n 的质数的数量。

 

示例 1：

输入：n = 10
输出：4
解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
示例 2：

输入：n = 0
输出：0
示例 3：

输入：n = 1
输出：0
 

提示：

0 <= n <= 5 * 106

public int countPrimes(int n) {
        int cnt=0;//计数
        //flag[]用来记录每个数字标志，从2开始初始化为1，若为非素数，则置为0
        int[] flag = new int[n];
        for(int i=2;i<n;++i){
            flag[i]=1;
        }

        for(int i=2;i<n;++i){

            if(flag[i]==1){
                for(int j=2;j*i<n;++j){
                    flag[i*j]=0;
                }

            }
        }

        for (int i=0;i<n;++i){
            if(flag[i]==1)
                cnt++;
        }
        return cnt;
    }

补充知识：

（1）数组初始化

Java语言中各类型变量的默认初始化值。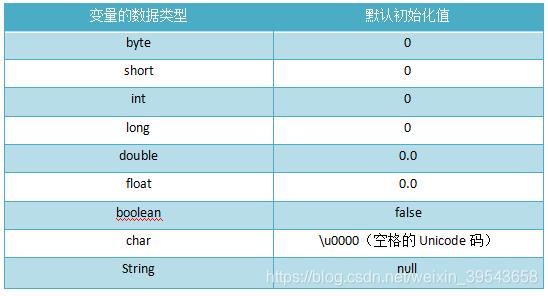

        byte[] array_one = new byte[1];
        short[] array_two = new short[1];
        int[] array_three = new int[1];
        long[] array_four = new long[1];
        System.out.println("代码输出：");
        System.out.println(array_one[0]);
        System.out.println(array_two[0]);
        System.out.println(array_three[0]);
        System.out.println(array_four[0]);

　结果：