前缀和差分双指针

Posted 2020-12-21 w-w-t

前缀和

前缀和就是数组前 $ i $ 项之和，主要作用是能快速求出 区间和

下标 ： (1) (2) (3) (4) (5)

(a[5]) : (2) (4) (3) (5) (8)

前缀和数组： (2) (6) (9) (14) (22)

为了便于计算，数组下标一般从 (1) 开始，能得到

一维数组前缀和公式：

[sum[i] = sum[i-1] + a[i] ]

    //构造前缀和数组
    for(int i = 1 ; i <= n ; i++){
        cin >> a[i];
        sum[i] = sum[i - 1] + a[i];
    }

对一维数组区间求和:

求区间 ([l , r]) 的数值之和 ， 一般的方法是从 (l) 遍历到 (r) 求总和

比如求上面数组 ([2 , 4]) 的区间和 ， (SUM = 4 + 3 + 5 = 12)

但有了前缀和数组 ，只需要用 前 (r) 个数的总和减去前 (l-1) 个数的总和

([2 , 4]) 的区间和 ， $SUM = sum[4] - sum[1] = 14 - 2 = 12 $

一维数组区间和公式：

[sum[l , r] = sum[r] - sum[l-1] ]

当然，有一维的，还有二维数组的前缀和，用于求子矩阵的和

二维数组前缀和公式：

[sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + a[i][j] ]

解释一下：

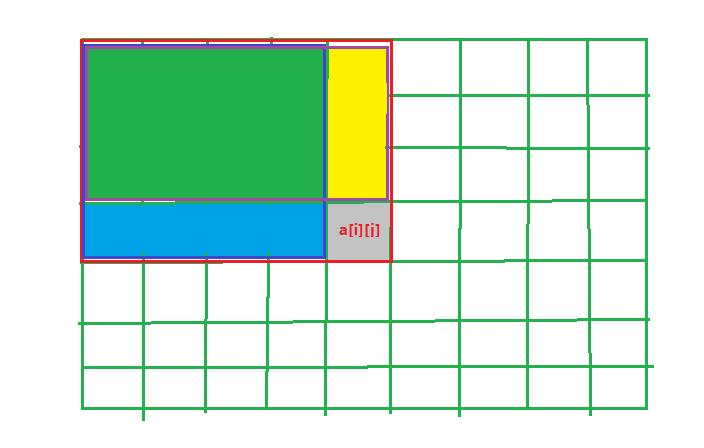
红色框代表(sum[i][j]) ，蓝色+绿色部分代表(sum[i][j-1]) ， 黄色+绿色部分代表(sum[i-1][j])

绿色部分代表(sum[i-1][j-1])

结合公式看图就能理解了。

怎么利用二维前缀和数组求子矩阵和呢

二维数组子矩阵求和公式：

[sum[(x1,y1),(x2,y2)] = sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1]+sum[x1-1][y1-1] ]

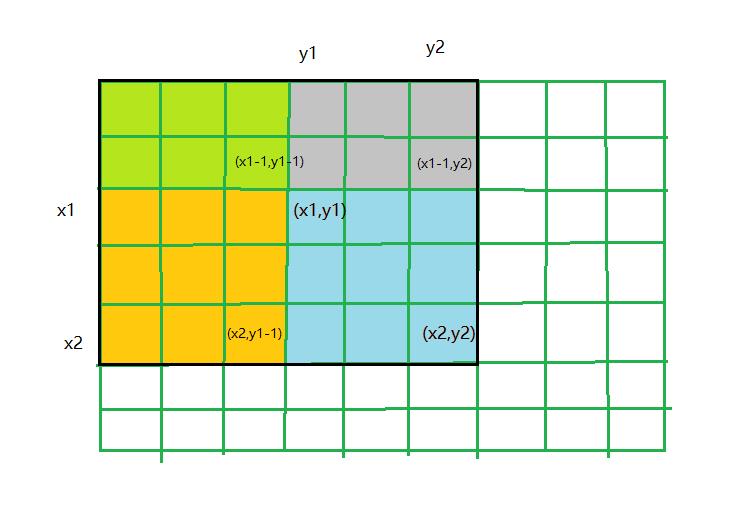
给出$(x1,y1) $和 ((x2,y2))，求子矩阵和 ( 也就是蓝色区域面积 ) ，结合公式看图理解。

例题：

最大子序和

K倍区间

激光炸弹

差分

差分指的就是当前值与前一个值的差值 (学的高数中有差分方程的概念，所以你们是接触过的)

下标 ： (1) (2) (3) (4) (5)

(a[5]) : (2) (6) (9) (14) (22)

差分数组 ： (2) (4) (3) (5) (8)

比较发现：a[5]相当于差分数组的前缀和数组

一维数组差分公式：

[b[i] = a[i] - a[i-1] ]

    //构造差分数组（方法1） 
    for(int i = 1 ; i <= n ; i++){
        cin >> a[i];
        b[i] = a[i] - a[i-1];
    }

后面还有另一种构造差分数组的方法

主要作用：快速处理区间加减操作

将对原序列的区间操作转换为对差分数组的单点操作

一般做法，遍历([l,r])

比如：我对 ([2,4]) 进行 (+1) 操作 ，就是给(a[2],a[3],a[4]) 都(+1)

利用差分数组，只需要给(b[l] + c) , (b[r+1]-c) 就好了

([2,4])进行+1操作 ， 给b[2] +1 ， b[5] - 1 就好了

好处就是，如果有多次区间加减操作，我们不需要多次遍历数组，只需要对差分数组进行单点操作，最后只需要给差分数组求一下前缀和，就能获得多次区间加减操作后的(a[])

我们可以把这步写成函数，之后调用就好了

一维数组差分加减操作：

//[l, r]区间进行加减操作(c为操作值)
void insert(int l , int r , int c){
    b[l] += c;
    b[r + 1] -= c;
}

假设 a ,b数组 一开始都为0 ，那么输入a[i]是不是相当于对区间 $[i,i] $ 加上(a[i])

那么就可以利用上面的函数构造差分数组

    //构造差分数组（方法2） 
    for(int i = 1 ; i <= n ; i++){
        int x;
		cin >> x;
		insert(i, i, x); 
    }

这样就将构造差分数组和进行加减操作都用一个函数来进行。

相应的还有二维差分

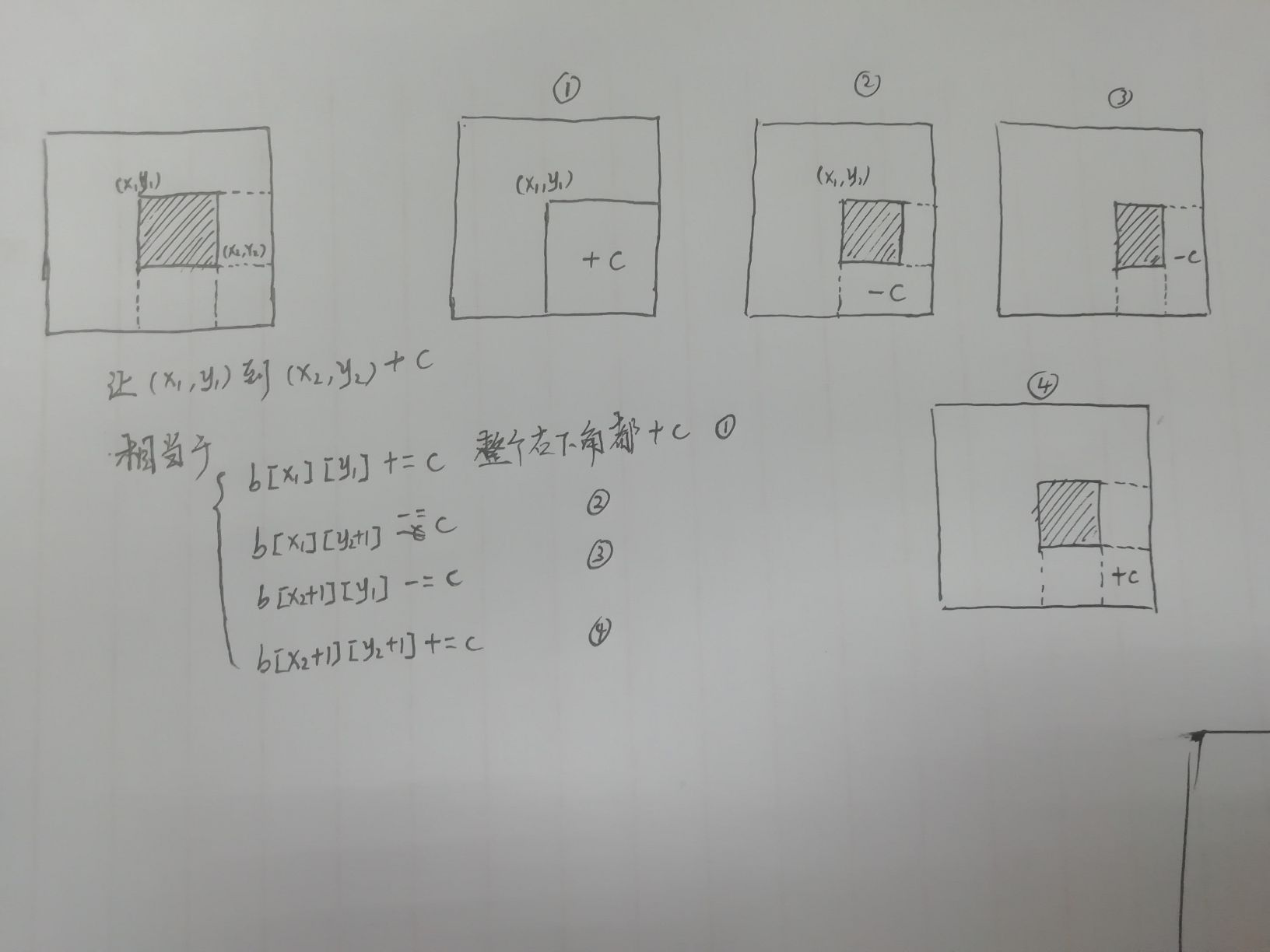
二维差分操作：

void insert(int x1,int y1,int x2,int y2,int c){
	b[x1][y1] += c;
	b[x1][y2+1] -= c;
	b[x2+1][y1] -= c;
	b[x2+1][y2+1] += c;
}

利用上面的函数，可以完成二维差分方程的构造以及各种操作

解释如下图：

例题：

AcWing 797.差分

IncDec Sequence

双指针（two pointers）

和上面两个一样，双指针算法也是一种思想，一种技巧，非常重要，我们也会经常用到双指针算法，比如归并排序中的区间合并，快速排序，还有我们熟悉的二分算法，都用到了双指针。

双指针,顾名思义，就是利用两个数组下标(i)，(j)，来代替原来一个数组下标遍历整个数组，以优化时间复杂度。

一般的写法

    for (int i = 0, j = 0; i < n ; i++)
    {
        while(j < i && check(i , j))
            j++;
        
        //然后是具体问题的分析

    }

例题： 输入一个英文句子，将每个单词单独作为一行输出。

代码：

#include <algorithm>
#include <cstdio>
#include <iostream>
#include <string>
using namespace std;
const int MA = 1e5 + 5;

int main()
{
    string str;
    getline(cin, str);
    int n = str.length();
    for (int i = 0; i < n; i++)
    {
        int j = i;
        while (j < n && str[j] != ‘ ‘)
            j++;
        //具体问题分析
        for (int k = i; k < j; k++)
            cout << str[k];
        cout << endl;
        i = j;
    }
    return 0;
}

最长连续不重复子序列

完整代码：(分析在下面)

#include<iostream>
#include <algorithm>
#include <cstdio>
#include<map>
using namespace std;
const int MA = 1e5 + 5;
int a[MA];
map<int,int> mp; //存每个值的个数
int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; ++i)
    {
        cin >> a[i];
    }
    int ans = 0;
    for (int i = 0, j = 0; i < n; ++i)
    {
        mp[a[i]]++;
        while (j < i && mp[a[i]] >= 2)
        {
            mp[a[j]]--;
            j++;
        }
        ans = max(ans, i - j + 1);
    }
    cout << ans << endl;
    return 0;
}

暴力的做法：

//暴力做法，时间复杂度O(n^2)
for(int i = 0 ; i < n ; i++)
{
    for(int j = 0 ; j <= i ; i++){
        if(check(j , i))
            ans = max(ans, i - j + 1);
    }
}

暴力的做法就是用(i) 作为子序列右端，用(j) 作为子序列左端 ， 判断是否满足条件，即从(j) 到 (i) 元素是否都只有1个，如果满足条件，更新结果。

双指针算法：

//双指针算法，时间复杂度O(n)
for(int i = 0 , j = 0 ; i < n ; i++)
{
    //check(j , i)为判断j到i之间是否有相同元素，有的话，j++
    while(j <= i && check(j , i))
        j++;
    ans = max(ans, i - j + 1);
}

大概思路：用(i) 指针将元素加进来 ， 用 j 指针来判断数组，不满足条件就去掉该元素 , j++

双指针算法如果想了解更多的话，去搜一些博客看看，然后找一题练一下。

例题：

完美序列

日志统计