希尔伯特空间

Posted 2020-12-20 cy0628

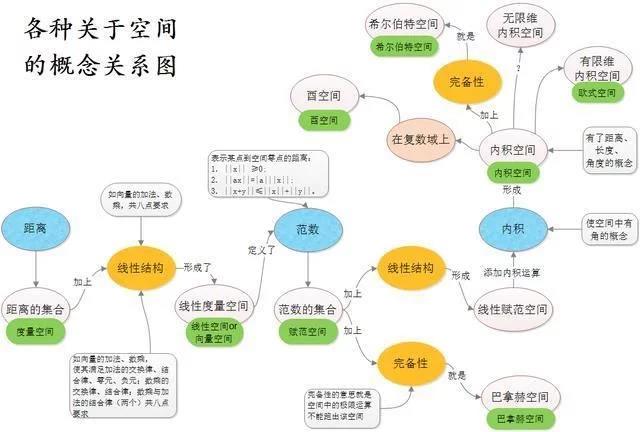
欧几里得空间，希尔伯特空间，巴拿赫空间或者是拓扑空间都属于函数空间。函数空间 = 元素 + 规则 ，即一个函数空间由元素 与元素所满足的规则 定义，而要明白这些函数空间的定义首先得从距离，范数，内积，完备性等基本概念说起。

1、度量空间：定义了距离的空间。

具体的距离：实际上距离除了我们经常用到的直线距离外，还有向量距离， 函数距离、 曲面距离、折线距离等等，这些具体的距离与距离之间的关系类似于苹果、香蕉等与水果的关系，前面是具体的事物，后面是抽象的概念。

距离就是一个抽象的概念，其定义为：
设X是任一非空集，对X中任意两点x,y，有一实数d(x,y)与之对应且满足：
1. d(x,y) ≥0，且d(x,y)=0当且仅当x=y;
2. d(x,y)=d(y,x);
3. d(x,y) ≤d(x,z)+d(z,y)。
称d(x,y)为X中的一个距离。

 

2、线性空间、向量空间

定义了距离后，我们再加上线性结构，如向量的加法、数乘，使其满足加法的交换律、结合律、零元、负元；数乘的交换律、单位一；数乘与加法的结合律（两个）共八点要求，从而形成一个线性空间，这个线性空间就是向量空间。

3、赋范空间

定义了范数，是绝对值（形式|a-b|）的延伸，是对向量、函数和矩阵定义的一种距离度量形式，如距离D(a,b)=||a?b||。

在向量空间中，我们定义了范数的概念，表示某点到空间零点的距离：
1. ||x|| ≥0;
2. ||ax||=|a|||x||;
3. ||x+y||≤||x||+||y||。

将范数与距离比较，可知，范数比距离多了一个条件2，数乘的运算，表明其是一个强化了的距离概念。范数与距离的关系可以类似理解为与红富士苹果与苹果的关系。

接下来对范数和距离进行扩展，形成如下：
范数的集合? 赋范空间 +线性结构?线性赋范空间
距离的集合? 度量空间 +线性结构?线性度量空间

4、内积空间、欧氏空间

下面在已经构成的线性赋范空间上继续扩展，添加内积运算，使空间中有角的概念，形成如下：
线性赋范空间+内积运算? 内积空间；
这时的内积空间已经有了距离、长度、角度等，有限维的内积空间也就是我们熟悉的欧氏空间。

什么是欧几里得空间？

古希腊数学家欧几里得创建了距离和角之间联系的法则——欧几里得几何，由二维平面几何可扩展成三维，再到有限维度抽象几何空间，称为欧几里得空间。其中维度是描述空间内一个点所需参量的个数——坐标数，例如三维空间中的点a=(x1,x2,x3)。

若把人的活动约束在学校，那么就是学校空间，同理，对点和几何结构进行各种约束，就构成了不同的数学空间。

 

至此，在各种约束条件下，有限维度+度量+线性+范数+内积=欧几里得空间。看似复杂的定义，其实就是一种约束的空间。

5、希尔伯特空间

继续在内积空间上扩展，使得内积空间满足完备性，形成希尔伯特空间如下：
内积空间+完备性? 希尔伯特空间
当欧几里德空间不再局限于有限维，就是希尔伯特空间——无限维度完备线性内积空间。完备指的是，空间中的极限运算衍生的所有可能点都包含于空间本身——柯西序列等价于收敛序列，简言之，合理即存在。

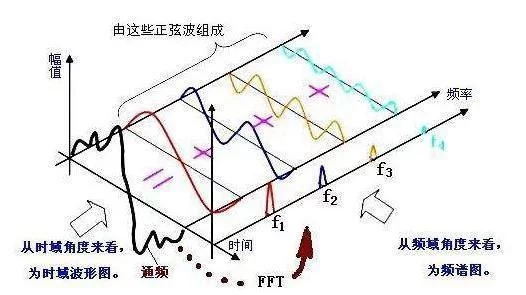
无限维度的向量（x1,x2,x3...xn）意味着有任意个独立坐标，可以用函数表达，两个无限维度的向量的内积等价于两个函数的积分。例如傅里叶变换，一种频率函数对应一个坐标，时域中每个点都可以在频域中展开成各种频率的函数。如此一来，欧几里得空间就演变成希尔伯特空间。

6、巴拿赫空间

此外，前面提到的赋范空间，使其满足完备性，扩展形成巴拿赫空间如下：
赋范空间+完备性? 巴拿赫空间

以上均是在距离的概念上进行添加约束形成的，递增关系如下：

距离?范数?内积 
向量空间+范数? 赋范空间+线性结构?线性赋范空间+内积运算?内积空间+完备性?希尔伯特空间 
内积空间+有限维?欧几里德空间 
赋范空间+完备性?巴拿赫空间

• 1
• 2
• 3
• 4

顺便提以下，对距离进行弱化，保留距离的极限和连续概念，就形成拓扑的概念。

参考：https://blog.csdn.net/weixin_36811328/article/details/81207753

            https://www.360kuai.com/pc/95f81d48af09ebadb?cota=4&kuai_so=1&sign=360_57c3bbd1&refer_scene=so_1

一.距离

       说到距离，我们首先想到的是点与点之间的距离，除此之外还有向量之间的距离，曲线之间的距离，函数之间的距离…。这儿谈到 距离 的定义是一种泛指的概念。点与点之间的距离 与 距离 就类似于苹果与水果之间的关系。距离 这个概念的作用主要用于衡量同一空间不同元素之间的差异情况，从这个出发点我们可以得到关于距离的一些属性：

1. 元素之间的距离大于等于0，若距离等于0则为相同元素。
2. 元素A到B之间的距离等于元素B到A之间的距离。
3. 元素之间的距离满足三角不等式。

满足以上三条属性即可称作元素之间的距离，其正式定义如下

      设X是一个非空集合，任给一对这一集合的元素$X,Y$。都给定一个实数 $d(X,Y)$ 与之对应，并且满足

1. $d(X,Y)\ge 0;d(X,Y)=0?X=Y;$
2. $d(X,Y)=d(Y,X);$
3. $d(X,Y)\le d(X,Z)+d(Y,Z);$

则称$d(X,Y)$是元素X,Y之间的距离

二.范数

       范数 是比 距离 限制条件更多的一个概念。为了形象地解释范数的概念，这儿在二维平面进行说明。
       在定义了 距离 这个概念之后，我们便可以描述二维平面上两个点之间的 距离 ，此时这个空间称作 度量空间 。但目前的条件没有办法描述一个点的“长度” ，因为缺少了 零点 。而范数定义之后此空间便多了一个零点，可以联想我们熟悉的平面直角坐标系，二维平面中范数可以看做是平面中的点到零点的距离。拥有范数的空间称作赋范空间，用符号$||X||$表示元素$X$的范数。因为范数的概念是在距离的概念上加了新的限制，则赋范空间一定是度量空间。我们可以用范数定义距离：$$d(X,Y)=||X?Y||$$
总结：元素$X$的范数$||X||$可简单看做$X$到零点的近距离。

三.线性

       线性这个概念可以说是很熟悉了，即为加法与乘法的结合。若一个空间为线性空间，只要我们知道了此空间的所有基，便可以用加法与数乘表示这一空间所有的元素，如二维平面中能用X轴的单位向量与Y轴的单位向量表示此平面的任意向量。

四.内积

       内积又称点积或者数量积，在高中学习向量的点乘运算时便接触到这一概念。在有了前面的定义之后的空间总觉得与我们最熟悉的空间还差点什么，没错，就是角度。在引入内积之后的空间便有了角度的概念。$X$与$Y$的内积用符号$(X,Y)$表示，内积的结果同样是为实数。内积是在范数的概念上加了更多限制条件，即内积空间一定为赋范空间，同样的，可以用内积定义范数如下：$$||X|{|}^2=(X,X)$$
       目前为止便完成了本文的大部分内容，有限维内积空间便是我们最熟悉的欧几里得空间。

五.完备性

       完备性这个概念的历史渊源比较深厚，作为非数学专业的工科生我也不太明白完备性的具体含义，简单来说对集合中的元素取极限不超出此空间便称其具有完备性。可以反向地通过不完备来理解完备性，对于整数集而言，对5取极限，便会超出整数集，即整数集不完备。
2018-10-22更正： 最近学了一点泛函，对完备性有了新的理解。完备性是在极限的基础上衍生的概念。例如在有理数集上的一个序列{1，1.4，1.41，1.414，1.4142…}，可知此序列极限为$\sqrt{2}$，而$\sqrt{2}$为无理数，不属于有理数集，即有理数集不具备完备性。

有了以上的概念理解众多迷糊人的空间便容易得多了

1. 线性完备内积空间称作希尔伯特空间
2. 线性完备赋范空间称作巴拿赫空间
3. 有限维线性内积空间称作欧几里得空间

       需要更加深入地理解希尔伯特空间大概避不开泛函分析，但作为工科学生，大概了解其概念够用就好。