LCA之倍增简单讲解

Posted 2020-12-19 what-the-heck

LCA之倍增简单讲解

LCA代指Least Common Ancestor，翻译过来就是最近公共祖先

如下图，x和y的最近公共祖先就是二号节点

 

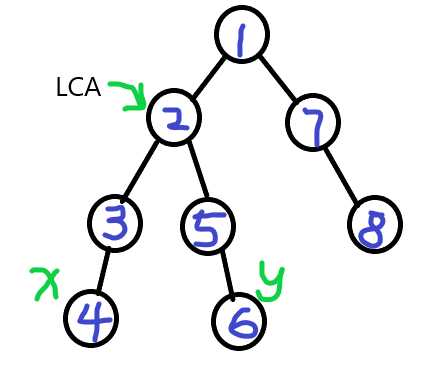
那么，如何来求这个最近公共祖先呢？

1.暴力算法

让x和y一步一步向上爬，一直爬到相遇为止

x: 4->3->2

y: 6->5->2

可是这样暴力实在是太慢了，我们要想办法优化它

于是就有了倍增求解LCA

2.倍增

倍增的意思就是按二的此方递增，比如： 1->2->4->8->16......

在x与y向上爬找祖先时，我们不用每次向上爬一个，而是向上爬2^n个，这样程序的效率会高很多

怎么倍增呢？我们需要从大到小跳，比如： 32->16->8->4...... 为什么不是从小到大？应为可能会跳过，出现“悔棋”的情况

举个例子：

 

 

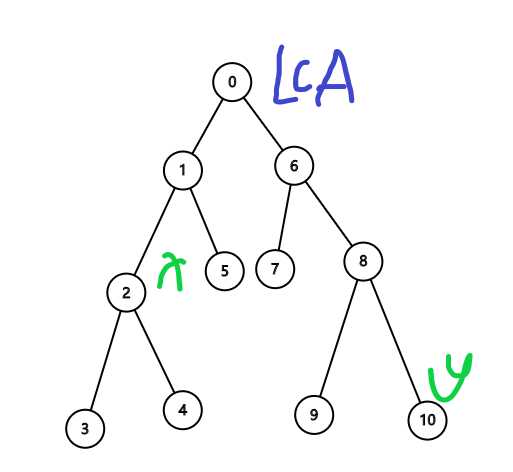
 我们要求x(5号节点)与y(10号节点)的 LCA

倍增的时候，我们发现y的深度比x的深度要小，于是现将y跳到8号节点，使他们深度一样：

 

 

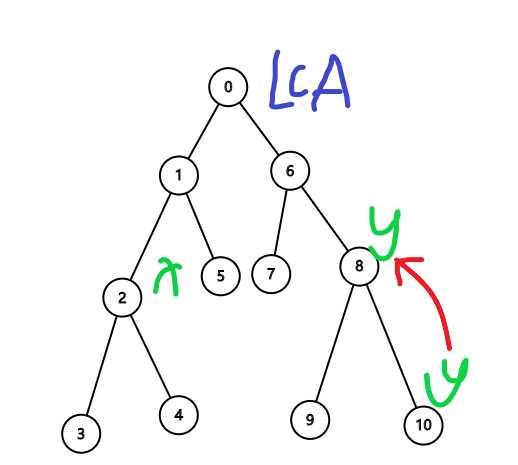
 这个时候，x和y的深度就相同了，于是我们按倍增的方法一起去找LCA

我们知道n（10）之内最大的二的次方是8，于是我们向上跳8个单位，发现跳过了。

于是我们将8/2变成4，还是跳过了。

再将4/2变成2，跳到了0号节点。

虽然这时跳到了LCA,但是如果直接if（x==y）就确定的话，程序无法判断是刚好跳到了还是跳过了，应为跳过了x也等于y

于是我们需要刚好跳到LCA的儿子上，然后判断if（x的爸爸==y的爸爸）来确定LCA

由于每一个数都可以分解为几个2^n的和（不信自己试），所以他们一定会跳到LCA的儿子上

于是我们就找到了LCA啦！

3.预处理

明白了基本思路之后，我们就开始写程序了

可是在写LCA之前，我们还得进行预处理

要处理些什么呢？

1.每一个点的深度，以便到时候判断

2.每一个点2^i级的祖先，以便到时候倍增跳

于是我们用一个dep数组来记录每一个点的深度，再用一个fa[i][j]表示节点i的2^j级祖先

dep数组的更新就是他爸爸的深度+1，但是如何更新fa数组呢？

fa[i][j]=fa[fa[i][j-1]][j-1]

这个式子是什么意思呢?

fa[i][j]就是i的2^j级祖先，那fa[i][j-1]就是i的2^（j-1）级祖先。

又因为我们知道2^(j-1)+2^(j-1)=2^j，i的2^（j-1）级祖先的2^（j-1）级祖先 就是i的2^j级祖先。

这就是这句话的意思。代码如下：

void dfs(int x,int father) //x为当前节点，father为他的爸爸
{
    dep[x]=dep[father]+1; //x的深度是他父亲的深度+1
    fa[x][0]=father; //2^0是1，x向上一个的祖先就是他爸爸
    for(int i=1;(1<<i)<=dep[x];i++) //1<<i就是2^i，当2^i小于x的深度时，枚举他的祖先
    {
        fa[x][i]=fa[fa[x][i-1]][i-1]; //上面说过的fa数组的更新
    }
    for(int i=0;i<e[x].size();i++) //枚举与他相邻的边（我用的是vector存图）
    {
        if(e[x][i]!=father) //如果不是他爸爸
        {
            dfs(e[x][i],x); //继续dfs
        }
    } 
    return;
}

4.LCA主函数

过程在上面已经讲过了，直接上代码：

int lca(int u,int v) //u,v就相当于先讲的x和y
{
    int temp; //temp是两个点的深度度差
    if(dep[u]<dep[v]) //我们默认u的深度大一些，否则将u与v交换
        swap(u,v);
    temp=dep[u]-dep[v]; //计算深度差
    for(int i=0;(1<<i)<=temp;i++) //将u的深度变得与v相同，还是使用倍增的思想
    {
        if((1<<i)&temp) //这个操作就相当于将深度差变成几个2^n的和，判断2^i是不是其中一个
        {
            u=fa[u][i]; //将u跳到他祖先的位置
        }
    }
    if(u==v) //如果u刚好等于v,即他们已经变成了同一个点
    {
        return u; //返回这个点的值,就是LCA
    }
    for(int i=(int)(log(n)/log(2));i>=0;i--) //(int)(log(n)/log(2))就是n以内最大的2的次方，从最大的开始倍增
    {
        if(fa[u][i]!=fa[v][i]) //如果他们的爸爸不相同，即没有找到LCA
        {
            u=fa[u][i]; 
            v=fa[v][i]; //一起倍增
        }
    }
    return fa[u][0]; //返回他们的爸爸，即是LCA   
}

 5.完整代码

下面是模板题洛谷p3379的代码：

 

#include <cmath>
#include <cstdio>
#include <vector> 
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn=500005;
vector <int> e[maxn];
int n,m,s,dep[maxn],fa[maxn][21];
int read() //快读 
{ 
    int ans=0,flag=1;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch==‘-‘)
            flag=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        ans=ans*10+ch-‘0‘;
        ch=getchar();
    } 
    return ans*flag; 
} 
void dfs(int x,int father) //x为当前节点，father为他的爸爸
{
    dep[x]=dep[father]+1; //x的深度是他父亲的深度+1
    fa[x][0]=father; //2^0是1，x向上一个的祖先就是他爸爸
    for(int i=1;(1<<i)<=dep[x];i++) //1<<i就是2^i，当2^i小于x的深度时，枚举他的祖先
    {
        fa[x][i]=fa[fa[x][i-1]][i-1]; //上面说过的fa数组的更新
    }
    for(int i=0;i<e[x].size();i++) //枚举与他相邻的边（我用的是vector存图）
    {
        if(e[x][i]!=father) //如果不是他爸爸
        {
            dfs(e[x][i],x); //继续dfs
        }
    } 
    return;
}
int lca(int u,int v) //u,v就相当于先讲的x和y
{
    int temp; //temp是两个点的深度度差
    if(dep[u]<dep[v]) //我们默认u的深度大一些，否则将u与v交换
        swap(u,v);
    temp=dep[u]-dep[v]; //计算深度差
    for(int i=0;(1<<i)<=temp;i++) //将u的深度变得与v相同，还是使用倍增的思想
    {
        if((1<<i)&temp) //这个操作就相当于将深度差变成几个2^n的和，判断2^i是不是其中一个
        { 
            u=fa[u][i]; //将u跳到他祖先的位置
        }
    }
    if(u==v) //如果u刚好等于v,即他们已经变成了同一个点
    {
        return u; //返回这个点的值,就是LCA
    }
    for(int i=(int)(log(n)/log(2));i>=0;i--) //(int)(log(n)/log(2))就是n以内最大的2的次方，从最大的开始倍增
    {
        if(fa[u][i]!=fa[v][i]) //如果他们的爸爸不相同，即没有找到LCA
        {
            u=fa[u][i]; 
            v=fa[v][i]; //一起倍增
        }
    }
    return fa[u][0]; //返回他们的爸爸，即是LCA   
}
int main()
{
    n=read();
    m=read();
    s=read();
    for(int i=1;i<=n-1;i++)
    {
        int x=read(),y=read();
        e[x].push_back(y);
        e[y].push_back(x); //vector存图 
    }
    dfs(s,0); //预处理 
    for(int i=1;i<=m;i++)
    {
        int x=read(),y=read();
        int ans=lca(x,y);
        printf("%d
",ans); 
    }
    return 0; 
} 

 

其他题目：

洛谷p3884 二叉树问题

洛谷p2420 让我们异或吧

洛谷p3398 仓鼠找sugar