代码源 Div1 - 105#451. Dis（倍增求LCA）

Posted 2022-04-07 小哈里

problem

solution

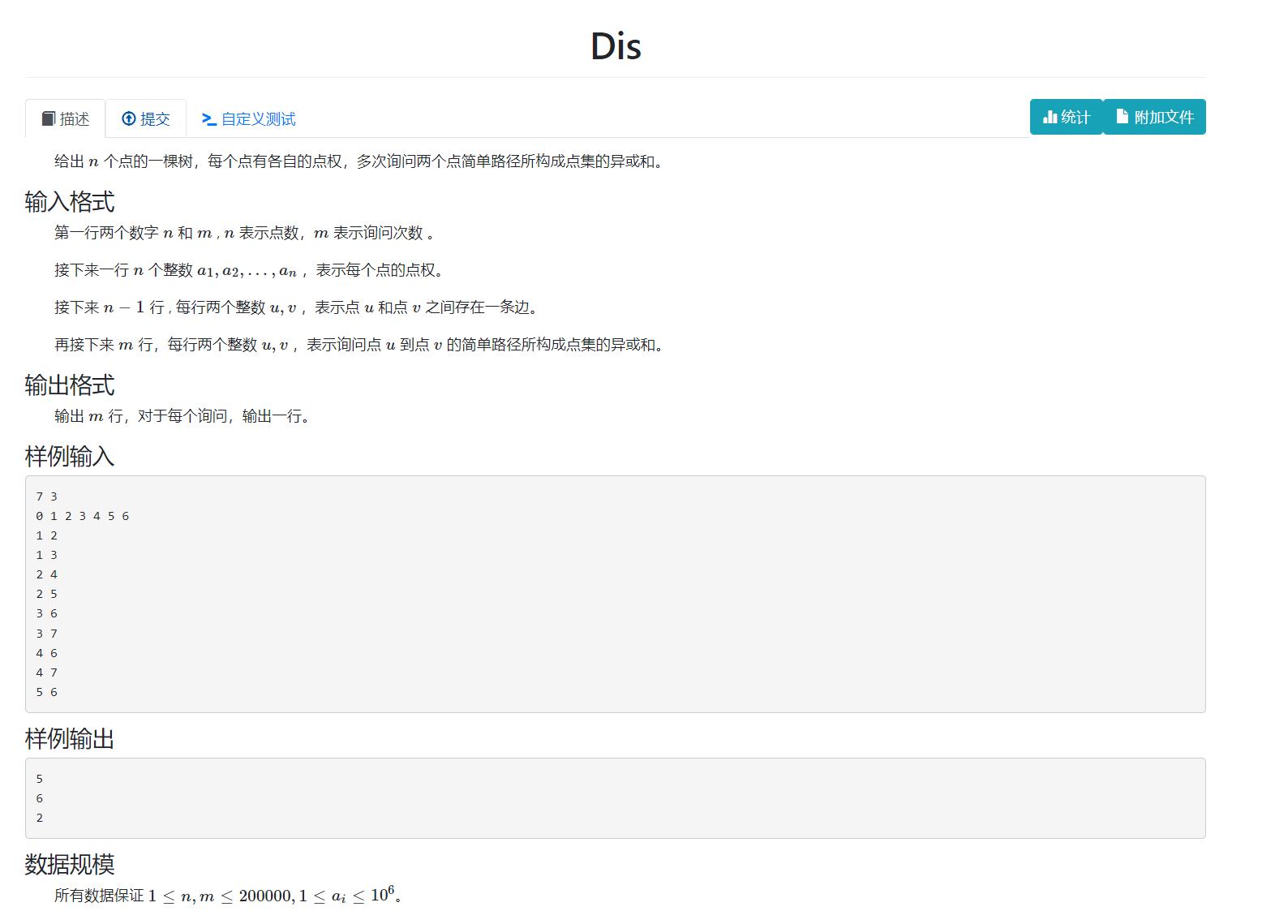
• 给出 n 个点的一棵树，每个点有各自的点权，m 次询问两个点简单路径所构成点集的异或和。
• 直接在树上求LCA，把每个点权放进去预处理一下即可。

#include<bits/stdc++.h>
using namespace std;

#define ios ios::sync_with_stdio(0), cin.tie(0),cout.tie(0)
typedef long long LL;
const LL maxn = 2e5+10;

int n, m;
int a[maxn];
vector<int>G[maxn];

int fa[maxn][20], dep[maxn], val[maxn][20];
void dfs(int u, int f, int d)
    fa[u][0] = f;
    val[u][0] = a[f];
    dep[u] = d;
    for(int x : G[u])
        if(x==f)continue;
        dfs(x,u,d+1);
    

void init()
    for(int i = 1; i < 20; i++)
        for(int j = 1; j <= n; j++)
            fa[j][i] = fa[fa[j][i-1]][i-1];
            val[j][i] = val[j][i-1]^val[fa[j][i-1]][i-1];
        
    

int lca(int x, int y)
    if(dep[x]<dep[y])swap(x,y);
    int ans = 0;
    for(int i = log2(dep[x]-dep[y]); i >= 0; i--)
        if((1<<i)<=dep[x]-dep[y])ans ^= val[x][i], x = fa[x][i];
    
    if(x == y)return ans^a[y];
    for(int i = log2(dep[x]); i >= 0; i--)
        if(fa[x][i] != fa[y][i])
            ans ^= val[x][i];
            ans ^= val[y][i];
            x = fa[x][i];
            y = fa[y][i];
        
    
    ans ^= val[x][0];
    return ans;


int main()
    IOS;
    cin>>n>>m;
    for(int i = 1; i <= n; i++)cin>>a[i];
    for(int i = 1; i < n; i++)
        int u, v;  cin>>u>>v;
        G[u].push_back(v);
        G[v].push_back(u);
    
    dfs(1,1,0);
    init();
    while(m--)
        int u, v;  cin>>u>>v;
        int ans = lca(u,v)^a[u]^a[v];
        if(u==v)cout<<a[u]<<"\\n";
        else cout<<ans<<'\\n';
    
    return 0;