TensorFlow框架之Computational Graph详解

Posted 2020-10-04

1. Getting Start

1.1 import

　　TensorFlow应用程序需要引入编程架包，才能访问TensorFlow的类、方法和符号。如下所示的方法：

import tensorflow as tf

2. Tensor

　　TensorFlow用Tensor这种数据结构来表示所有的数据。可以把一个Tensor想象成一个n维的数组或列表。Tensor有一个静态的类型和动态的维数。Tensor可以在图中的节点之间流通。

2.1 秩（Rank）

　　Tensor对象由原始数据组成的多维的数组，Tensor的rank（秩）其实是表示数组的维数，如下所示的tensor例子：

Rank	数学实例	Python 例子
0	常量 (只有大小)	s = 483
1	向量(大小和方向)	v = [1.1, 2.2, 3.3]
2	矩阵(数据表)	m = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
3	3阶张量 (数据立体)	t = [[[2], [4], [6]], [[8], [10], [12]], [[14], [16], [18]]]
n	n阶 (自己想想看)	…

2.2 形状（Shape）

　　TensorFlow为了描述Tensor每一维的长度，相当于描述每一维数组的长度，所以定义了Shape概念。其可以描述Tensor的维数，又可以描述每一维的长度。

Rank	Shape	Dimension number	Example
0	[]	0-D	一个常量.
1	[D0]	1-D	[5]：表示一个向量有5个元素
2	[D0, D1]	2-D	[3, 4]：表示一个矩阵，共有3*4个元素
3	[D0, D1, D2]	3-D	[2, 4, 3]：总共有2*4*3个元素
n	[D0, D1, D2,… DN-1]	n-D	….

2.3 类型（Data type）

　　除了维度，Tensor有一个数据类型属性，你可以为一个张量指定下列数据类型中的任意一个类型，但是一个Tensor所有元素的类型必须相同。

数据类型	Python 类型	描述
DT_FLOAT	tf.float32	32 位浮点数.
DT_DOUBLE	tf.float64	64 位浮点数.
DT_INT64	tf.int64	64 位有符号整型.
DT_INT32	tf.int32	32 位有符号整型.
DT_INT16	tf.int16	16 位有符号整型.
DT_INT8	tf.int8	8 位有符号整型.
DT_UINT8	tf.uint8	8 位无符号整型.
DT_STRING	tf.string	可变长度的字节数组.每一个张量元素都是一个字节数组.
DT_BOOL	tf.bool	布尔型.
DT_COMPLEX64	tf.complex64	由两个32位浮点数组成的复数:实数和虚数.
DT_QINT32	tf.qint32	用于量化Ops的32位有符号整型.
DT_QINT8	tf.qint8	用于量化Ops的8位有符号整型.
DT_QUINT8	tf.quint8	用于量化Ops的8位无符号整型.

 

3. Computational graph

3.1 定义

　　Computational graph 是由一系列边（Tensor）和节点（operation）组成的数据流图。每个节点都是一种操作，其有0个或多个Tensor作为输入边，且每个节点都会产生0个或多个Tensor作为输出边。即节点是将多条输入边作为操作的数据，然后通过操作产生新的数据。可以将这种操作理解为模型，或一个函数，如加减乘除等操作。

　　简单地说，可以将Computational graph理解为UML的活动图，活动图和Computational graph都是一种动态图形。TensorFlow的节点（操作）类似活动图的节点（动作），TensorFlow每个节点都有输入（Tensor），可以将用户创建的起始Tensor看做是活动图的起始节点，而TensorFlow最终产生的Tensor看做是活动图的终止节点，如图 31所示。

 

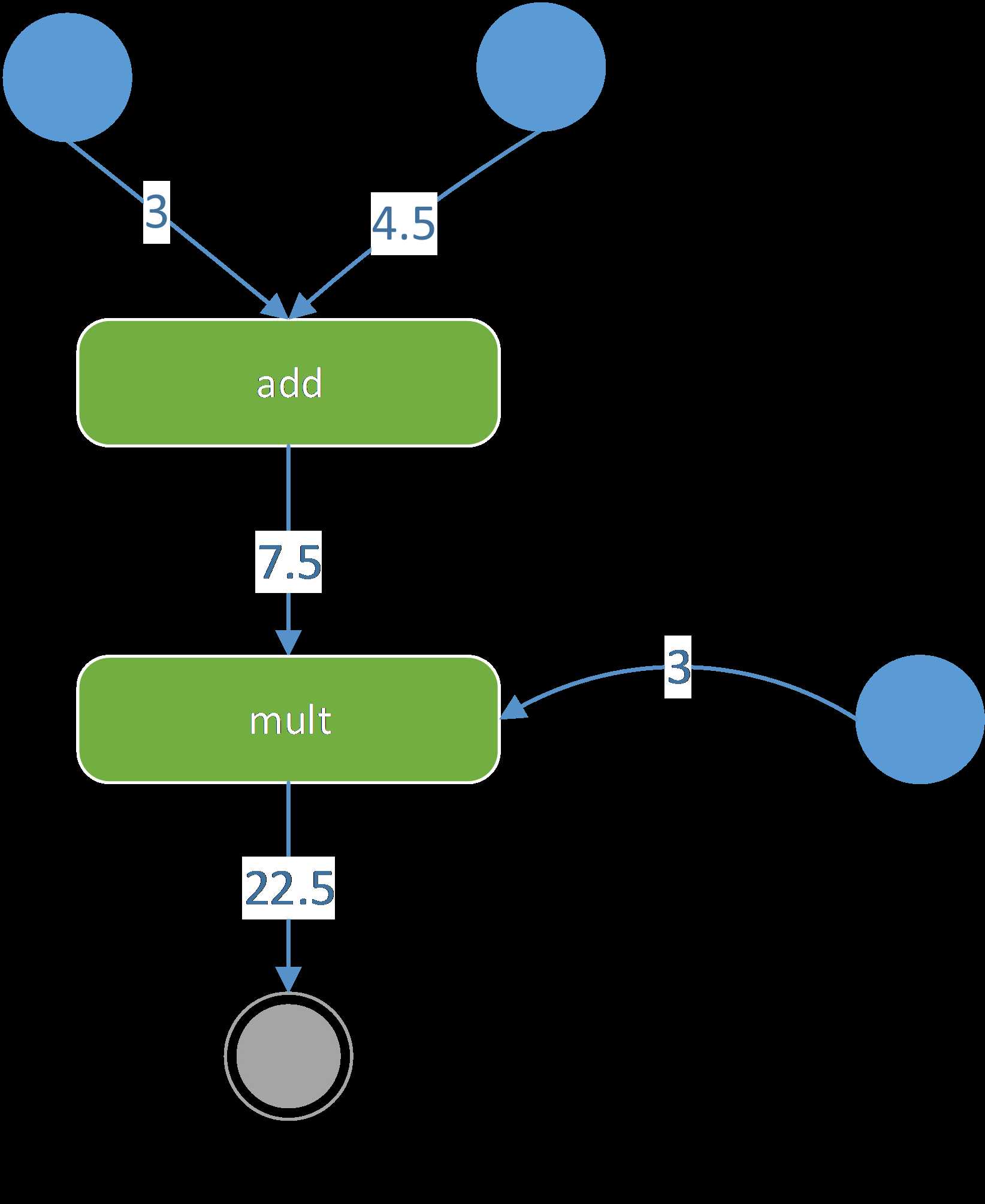
图 31

　　图 31所示，常量3和常量4.5两个起始Tensor通过add操作后产生了一个新Tensor（值7.5）；接着新Tensor（值7.5）和常量3经multi操作后产生一个新Tensor（值22.5），因为22.5是TensorFlow最后产生的Tensor，所以其是终止节点。

3.2 Session

　　TensorFlow通过一个对象（Session）来管理Computational graph 节点动态变换。由于Tensor是一种数据结构，为了获取Tensor存储的数据，需要手动调用Session对象的run方法获得。

　　实现一个TensorFlow应用程序，用户需要进行两个步骤：

　　1) 建立计算图（Building the computational graph）

　　　　Computational Graph建立其实是建立节点和边的一些依赖关系，这个过程是建立一种静态结构。

　　2) 执行计算图（Running the computational graph）

　　　　Computational Graph执行其实就是调用session.run()方法。由于Computational Graph是有边和节点组成，所以可以向run方法传递的两种参数：

• 边（Tensor）：若传递的是Tensor对象，则是获取Tensor对象的数据；
• 节点：若传递的是节点，则会先获取节点返回的Tensor对象，然后再获取Tensor对象的数据。

　　综上所述执行Computational Graph其实是获取Tensor的数据。在执行Tensor对象数据时，会根据节点的依赖关系进行计算，直至初始节点。

如下建立两个TensorFlow节点，节点的类型是constant，然后通过add操作后产生一个新节点，如下所示：

##1.建立computational graph node1 = tf.constant(3., tf.float32) node2 = tf.constant(4.5) tensor = tf.add(node1, node2)   print(node1) print(node2)   ##2.执行computational graph session = tf.Session() print(session.run(node1)) print(session.run(node2)) print(session.run(tensor))

输出： Tensor("Const:0", shape=(), dtype=float32) Tensor("Const_1:0", shape=(), dtype=float32) 3.0 4.5 7.5

图 32

注意：

• 在执行computational graph之前，TensorFlow节点是一种静态结构，所以输出的并不是3.0和4.0，而是tensor对象；
• 在执行computational graph之后，才输出了节点的值，即为了让某个节点从初始节点开始变换，需要通过Session对象的run方法手动变换。

3.3 InteractiveSession

　　文档中的 Python 示例使用一个会话 Session 来 启动图, 并调用 Session.run() 方法执行操作.为了便于使用诸如 IPython 之类的 Python 交互环境, 可以使用 InteractiveSession 代替 Session 类, 使用 Tensor.eval() 和 Operation.run() 方法代替 Session.run(). 这样可以避免使用一个变量来持有会话.

# 进入一个交互式 TensorFlow 会话. import tensorflow as tf sess = tf.InteractiveSession()   x = tf.Variable([1.0, 2.0]) a = tf.constant([3.0, 3.0])   # 使用初始化器 initializer op 的 run() 方法初始化 ‘x‘ x.initializer.run()   # 增加一个减法 sub op, 从 ‘x‘ 减去 ‘a‘. 运行减法 op, 输出结果 sub = tf.sub(x, a) print sub.eval() # ==> [-2. -1.]

4. 起始节点

　　目前了解的，TensorFlow有三种类型的起始节点：constant（常量）、placeholder（占位符）、Variable（变量）。

4.1 常量 (constant)

　　TensorFlow的常量节点是通过constant方法创建，其是Computational Graph中的起始节点，在图中以一个圆点表示，如图 32所示。

如下述程序中所示，直接创建，但创建的节点不会开始执行，需要由Session对象的run方法开始启动。

tensor1 = tf.constant(3., tf.float32) print(tensor1)   tensor2 = tf.constant([1, 2, 3, 4, 5, 6, 7]) print(tensor2)   tensor3 = tf.constant(-1.0, shape=[2, 3]) print(tensor3)   session = tf.Session() print(session.run(tensor1)) print(session.run(tensor2)) print(session.run(tensor3))

输出： Tensor("Const:0", shape=(), dtype=float32) Tensor("Const_1:0", shape=(7,), dtype=int32) Tensor("Const_2:0", shape=(2, 3), dtype=float32) 3.0 [1 2 3 4 5 6 7] [[-1. -1. -1.] [-1. -1. -1.]]

4.2 占位符 (placeholder)

　　TensorFlow的placeholder节点是由placeholder方法创建，其也是一种常量，但是由用户在调用run方法是传递的，也可以将placeholder理解为一种形参。即其不像constant那样直接可以使用，需要用户传递常数值。

如下所示在执行node3：

import tensorflow as tf   node1 = tf.placeholder(tf.float32) node2 = tf.placeholder(tf.float32) tensor = tf.add(node1, node2)   print(node1) print(node2)   session = tf.Session() print(session.run(tensor, {node1:3,node2:4} ))

输出： Tensor("Placeholder:0", dtype=float32) Tensor("Placeholder_1:0", dtype=float32) 7.0

注意：

    由于在执行node3节点时，需要node1和node2作为输入节点，所以此时需要传递"实参"，即3和4.

图 41

4.3 变量 (Variable)

　　TensorFlow的Variable节点是通过Variable方法创建，并且需要传递初始值。常量在执行过程中无法修改值，变量可以在执行过程修改其值。但是TensorFlow的变量在创建之后需要再进行手动初始化操作，而TensorFlow常量在创建时就已进行了初始化，无需再进行手动初始化。

如下示例，创建两个变量，分别初始化为0.3和-0.3，然后传入一个向量值，最后计算出一个新的向量：

from __future__ import print_function import tensorflow as tf   w = tf.Variable([.3], tf.float32) b = tf.Variable([-.3], tf.float32) x = tf.placeholder(tf.float32)   linear = w * x + b   session = tf.Session() init = tf.global_variables_initializer() session.run(init)   print(session.run(linear, {x: [1, 2, 3, 4]}))

输出： [ 0. 0.30000001 0.60000002 0.90000004]

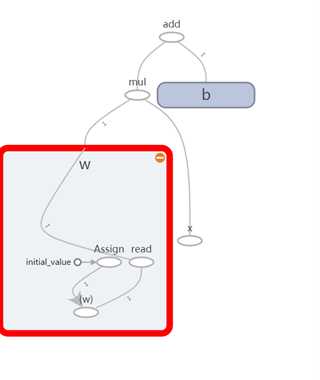
图 42

从W展开细节看，变量其实只是一个命名空间，其内部由一系列的节点和边组成。同时有一个常量节点，即初始值节点。

5. 模型评估

　　模型评估是指比较期望值和模型产生值之间的差异，若差异越大，则性能越差；差异越小，性能越好。模型评估有很多种方法，如均分误差或交差熵。

如下以常用的"均分误差"法举例说明，其等式为：

Y为期望向量，X为输入向量，f(X）为计算向量，如下所示：

from __future__ import print_function import tensorflow as tf #1. 构建计算流图 w = tf.Variable([.3], tf.float32) b = tf.Variable([-.3], tf.float32) x = tf.placeholder(tf.float32) y = tf.placeholder(tf.float32) #期望向量 linear_model = w * x + b   squared_deltas = tf.square(linear_model - y) #对两个向量的每个元素取差并平方，最后得出一个新的向量 loss = tf.reduce_sum(squared_deltas) #对向量取总和   #2. 执行计算流图 session = tf.Session() init = tf.global_variables_initializer() session.run(init)   print(session.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))

输出：           23.66

注意：

loss的值是依赖W、B和Y三个向量的值，所以计算loss Tensor会根据依赖关系获取W、B和Y三个Tensor的值，其计算流程图如图 51所示：

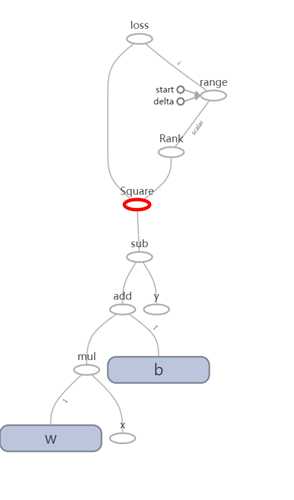
图 51

6. 优化

　　优化是指减少期望值与模型产生值之间的差异，即减少均分误差或交差熵的计算结果，如减少上述的loss变量值。

6.1 手动优化

　　我们可以通过修改上述的w和b的变量值，来手动优化上述的模型。由于TensorFlow的变量是通过tf.Variable方法创建，而重新赋值是通过tf.assign方法来实现。注意修改变量的动作需要执行Session.run方法来开始执行。

比如可以修改w=-1，b=1参数来优化模型，如下

from __future__ import print_function import tensorflow as tf   w = tf.Variable([.3], tf.float32) b = tf.Variable([-.3], tf.float32) x = tf.placeholder(tf.float32) y = tf.placeholder(tf.float32 ") linear_model = w * x + b   squared_deltas = tf.square(linear_model - y) loss = tf.reduce_sum(squared_deltas)   session = tf.Session() init = tf.global_variables_initializer() session.run(init)   #1.变量w和b初始值为3和-3时，计算loss值 print(session.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))   #2.重置变量w和b值为-1和1时，再计算loss值 fixw = tf.assign(w,[-1.]) fixb = tf.assign(b,[1.]) session.run(fixw) session.run(fixb) print(session.run(loss, {x:[1,2,3,4],y:[0,-1,-2,-3]}))

输出： 23.66 0.0

注意：

    loss的值是依赖W、B和Y三个向量的值来计算，即每次计算loss都需要上述三个变量的值进行计算。由于通过调用Session.run()方法来执行某个节点（Computational graph的节点为操作）时，会自动根据节点前后依赖关系，自动从初始节点开始计算到该节点。在第一次执行session.run(loss)时，W和B的值是3和-3；第二次执行session.run(loss)时，W和B的值被修改为-1和1后。所以session.run(loss)时会自动根据W和B的不同进行计算。

 

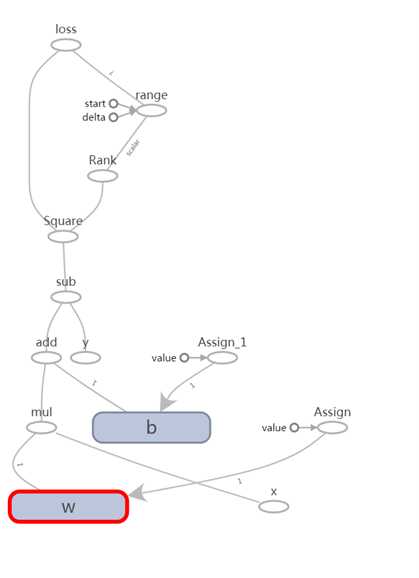
图 61

6.2 自动优化

　　上述通过手动调整变量w和b的值来改善模型的执行性能，虽然也行的通，但是非常单调且工作量太大。所以TensorFlow提供一些优化器（optimizers）来提高用户的工作效率，可以自动完成优化，即可以自动更新相关变量的值。

如下所示，以最简单的优化器gradient descent为例，其可以根据执行loss值逐渐修改每个变量值，：

import numpy as np import tensorflow as tf w = tf.Variable([.3], tf.float32) b = tf.Variable([-.3], tf.float32) x = tf.placeholder(tf.float32) linear_model = w * x + b y = tf.placeholder(tf.float32)   squared_deltas = tf.square(linear_model - y) loss = tf.reduce_sum(squared_deltas)   #1. optimizer optimizer = tf.train.GradientDescentOptimizer(0.01) train = optimizer.minimize(loss)   #2. training loop init = tf.global_variables_initializer() session = tf.Session() session.run(init)   for i in range(1000): session.run(train, {x:[1,2,3,4], y:[0, -1, -2, -3]})   #3. evaluate training accuracy curr_w, curr_b, curr_loss = session.run([w,b,loss], {x:[1, 2, 3, 4], y:[0, -1, -2, -3]}) print("w:%s b:%s loss:%s"%(curr_w,curr_b,curr_loss))

输出： w:[-0.9999969] b:[ 0.99999082] loss:5.69997e-11

注意：

　　1) optimizer：创建一个优化器，并指定优化的方向；优化器的优化过程是：对于方程中的权值（w）和偏置（b）对跟进loss值进行调整，v是泛指w或b参数，则每趟优化过程都会按如下方程更改w或b的值：

则dV是参数调整数幅度，如若v是权值w，则

　　2) training：执行优化器，在执行过程中会不断更新涉及的变量，即会更新W和B两个Tensor值；

　　3) evaluate：W和B在优化前就有初始值；在优化后会更新两个值；所以再执行loss时，会根据W、B和Y三个Tensor值来计算。

如图 62所示是产生的Computational graph图变换：

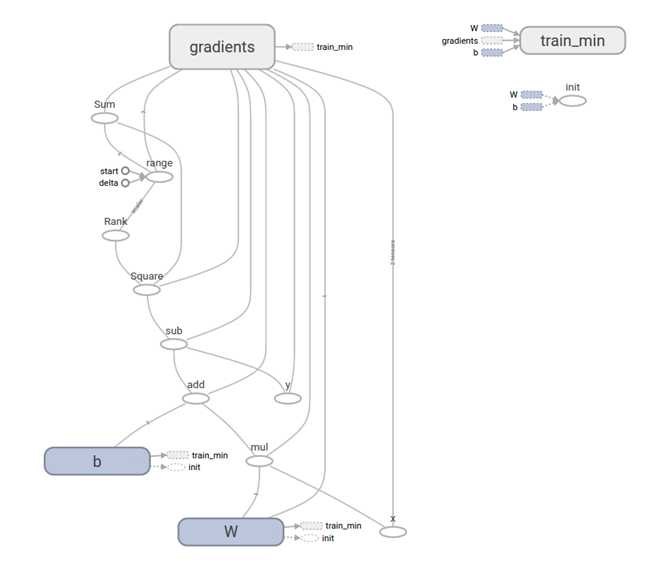
图 62

图中带有箭头的边缘是指依赖，如节点b有一个指向tain_min节点，表明b的值依赖tain_min节点。