数学建模 数据处理模型之变量相关性类（灰色相关联相关性分析）

Posted 2020-12-16 runrun225

相关类

灰色关联

1作用：系统分析主要因素；次要因素，因素对系统发展的影响，以便对各因素强化发展或者抑制发展。

2 灰色关联分析的基本思想：根据序列曲线的几何形状的相似程度判断其联系紧密性

3 具体操作步骤：

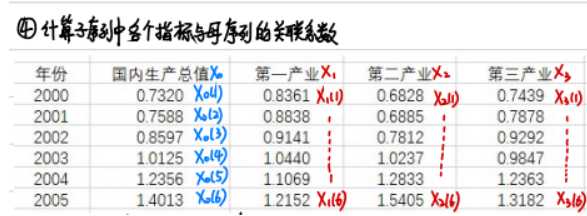
（1）绘图：各指标，各系统的发展趋势

（2）确定分析数列：

母序列：能反映系统行为特征的数据序列。（因变量），常用X或x0表示。

子序列：影响行为的因素组成的数据序列。（自变量），常用x1,x3,x3……表示

（此种方法下，母子序列的横纵坐标往往一样，取点取纵坐标）

（3）预处理分析数列：

计算均值，再用该指标每个元素都除以其均值。

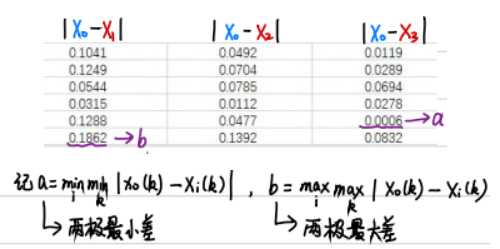
(4)计算关联系数

 

 a.x(0)-x(i)

 

 

 

 

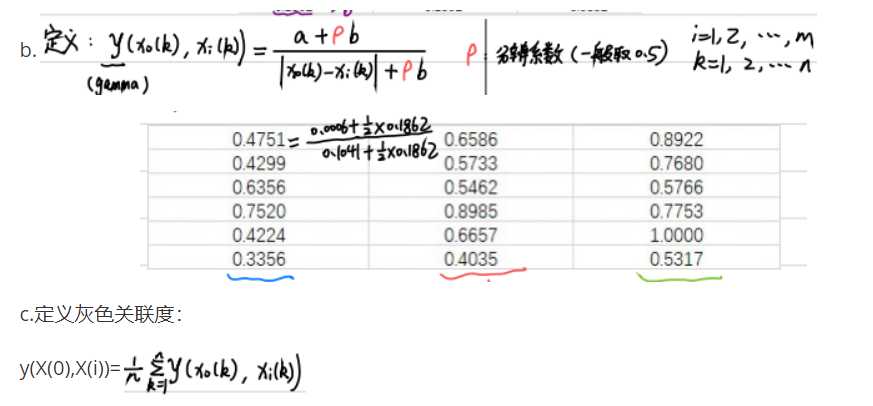
(5)由关联度得出二者之间的关联性。

(6)关联性往往用于确定权重

相关性分析

针对问题：在确定两个变量线性相关的前提条件下，通过相关系数判断他们的相关程度如何。（皮尔逊相关系数越大，相关性越强，反之越小）

相关系数的计算

 

 

对相关系数进行假设检验

步骤：

1 提出原假设H0和备择假设H1；即对相关系数r做出一个假设。

2 将我们要检验的量（里面相关系数和样本值，其中相关系数为随机变量）构造出一个符合某一分布的统计量（未代入前，相关系数就是上面公式的代入，因而是随机变量）

满足的分布可是：正态分布，t分布，卡方分布等

检验数据是否为正态分布：

（1）正态JB分布：

 

2）Q-Q图

做出Q-Q鉴别图，观察样本数据是否近似在一条直线附近，若是则近似于正态分布。

3 将要检验的值（样本，相关系数）代入统计量中

4 根据统计量的分布情况，由置信水平确定原假设成不成立。