数学建模之灰色关联分析（GRA）

Posted 2022-02-05 Icy Hunter

本文参考的是司守奎，孙兆亮主编的数学建模算法与应用（第二版）

灰色关联分析不仅能够用做关联分析，也能够用于评价。
其具体分析步骤如下：

第一步，需要确定评价对象和参考数列。
评价对象一般指的就是待分析的各个特征组，例如需要评价一个同学的成绩，那么他的语文成绩、数学成绩、英语成绩等就是一个特征组，即一个评价对象。
参考数列有两种选择，一种是从各个特征组中抽取出各自特征最优的值，构成一个虚拟的最优方案，并将此作为参考数列，那么其他方案都是参考最优方案得出的关联系数，即能够作为方案的评价，这也很容易理解，与最优方案关联越大，说明这个方案实际也是越优的。另一种是将待分析的方案中，挑选一组方案作为参考数列，例如需要分析小红、小明、小兰三者之间小红的成绩的和谁的关系比较大，那么就可以以小红的成绩作为参考数列，进行关联性分析，分析出的关联系数即可说明小红的成绩与谁的相关性越大，从而分析谁对小红的影响比较大（这是我随便举得例子，也不知道恰不恰当）

第二步，可以通过熵权法、层次分析法等确定权重，一般这里取等权重即可。

第三步，计算灰色关联系数。其中分辨系数一般取0.5即可

第四步，计算加权关联度。

第五步，评价分析。

接下来展示一个例题

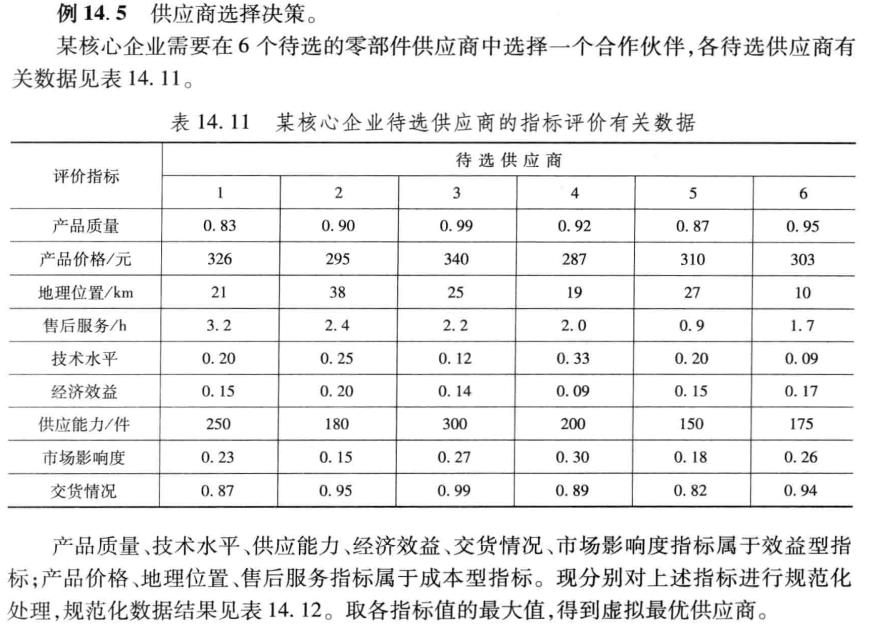
其实最开始，需要进行的步骤是对数据进行预处理，这是任何任务顺利进行下去不可或缺的环节。对于这题，数据预处理主要是将效益型指标归一化以及将成本型指标归一化为效益型的形式，即通过数值大小直接能够反应此指标的优劣。

data = [0.83 0.90 0.99 0.92 0.87 0.95
    326 295 340 287 310 303
    21 38 25 19 27 10
    3.2 2.4 2.2 2.0 0.9 1.7
    0.20 0.25 0.12 0.33 0.20 0.09
    0.15 0.20 0.14 0.09 0.15 0.17
    250 180 300 200 150 175
    0.23 0.15 0.27 0.30 0.18 0.26
    0.87 0.95 0.99 0.89 0.82 0.94];

%效益型指标归一化
for i =[1 5:9]
    data(i,:) = (data(i,:)-min(data(i,:)))/(max(data(i,:))-min(data(i,:)));
end
%成本型指标归一化
for i = 2:4
    data(i,:) = (max(data(i,:))-data(i,:))/(max(data(i,:))-min(data(i,:)));
end

预处理后结果如下：

接下来开始灰色关联分析。
第一步，确定评价对象和参考数列，由于我们是用于评价，那么评价对象就为各个方案，参考数列即为虚拟最优方案，即各个实际方案的最优值。

[row,col] = size(data);
cankao = max(data')'; %获取参考数列
cankao %由于评价这里取虚拟最优方案作为参考数列

可得参考数列：

第二步，确定权重，可以通过熵权法、层次分析法等确定权重，一般这里取等权重即可。

第三步，计算关联系数。分辨系数一般取0.5即可

t = repmat(cankao,[1,col])-data;%求参考序列与每一个序列的差
mmin = min(min(t));%计算最小差
mmax = max(max(t));%计算最大差
rho = 0.5;%分辨系数
xishu = (mmin + rho * mmax)./(t + rho * mmax)%计算灰色关联分析

第四步，计算加权关联度，由于我们权重为等权重，即权重都为1，那么直接取均值即可。

guanliandu = mean(xishu)%取等权重，计算关联度

第五步，评价分析。

[gsort,ind] = sort(guanliandu,'descend')%对关联度从大到小排序

结果如下：

matlab完整代码如下：

clc,clear
data = [0.83 0.90 0.99 0.92 0.87 0.95
    326 295 340 287 310 303
    21 38 25 19 27 10
    3.2 2.4 2.2 2.0 0.9 1.7
    0.20 0.25 0.12 0.33 0.20 0.09
    0.15 0.20 0.14 0.09 0.15 0.17
    250 180 300 200 150 175
    0.23 0.15 0.27 0.30 0.18 0.26
    0.87 0.95 0.99 0.89 0.82 0.94];

%效益型指标归一化
for i =[1 5:9]
    data(i,:) = (data(i,:)-min(data(i,:)))/(max(data(i,:))-min(data(i,:)));
end
%成本型指标归一化
for i = 2:4
    data(i,:) = (max(data(i,:))-data(i,:))/(max(data(i,:))-min(data(i,:)));
end

[row,col] = size(data);
cankao = max(data')'; %获取参考数列
cankao %由于评价这里取虚拟最优方案作为参考数列

t = repmat(cankao,[1,col])-data;%求参考序列与每一个序列的差
mmin = min(min(t));%计算最小差
mmax = max(max(t));%计算最大差
rho = 0.5;%分辨系数
xishu = (mmin + rho * mmax)./(t + rho * mmax)%计算灰色关联分析
guanliandu = mean(xishu)%取等权重，计算关联度
[gsort,ind] = sort(guanliandu,'descend')%对关联度从大到小排序