行列式

Posted 2020-12-16 luofeiju

行列式使用如下性质定义

1 单位矩阵行列式值为 1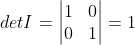，，对于任意单位矩阵均成立；

2 当矩阵交换一行后，行列式值改变符号，如置换矩阵的行列式值为 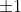（根据行交换次数决定）；

3 矩阵任意行线性变换导致行列式值产生线性变换：

   ， ；

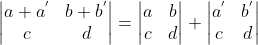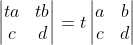使用以上三条基本性质，可以推导更多性质：

4 如果矩阵两行相等，行列式值为 0；

   利用性质2，交换两相等行，行列式值改变符号，故行列式值必须为 0；

5 对矩阵任意两行做如下运算：行2 = 行2 - k * 行1，新矩阵行列式值不发生改变，

   利用性质3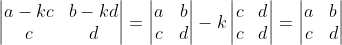， ；通过该性质，可以知道矩阵消元法仅改变矩阵行列式值的符号，；

 

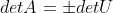6 如果矩阵中存在一行全为 0， 矩阵行列式值为 0；

   利用性质5，将全零行改写为任意非零行与全零行的和，得到两个全零行，故原矩阵行列式值为 0；

7 上三角矩阵或者下三角矩阵行列式值为对角元素之积，；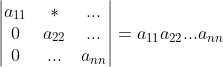

  1）利用性质5，使用消元法可以对非零元素进行消元处理，最终形成对角矩阵，其对角元素保持不变，即 det U = det D；

  2）利用性质3， ;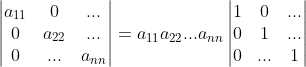

  3）利用性质1，由于 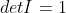，则上三角矩阵行列式值为为对角元素之积；

8 如果矩阵为奇异矩阵，行列式值为 0；如果矩阵为非奇异矩阵，行列式值不为 0；

  当矩阵为奇异矩阵时，使用消元法至少一行全零行，性质5 表明 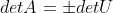, 根据性质6，det U = 0；

  当矩阵为非奇异矩阵时，使用消元法得到满秩，性质5 表明 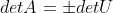，根据性质7得 ；

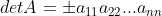9 矩阵乘积的行列式等于矩阵行列式的乘积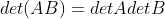，；使用该性质，有 ，；

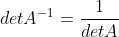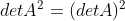   1）构造 ；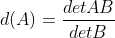

   2）当 A 为单位矩阵时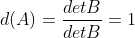，，满足性质1；

   3）当交换矩阵 A 中任意两行，矩阵 AB 中对应两行也发送交换，d(A) 符号发生改变，满足性质2；

   4）矩阵 A 中任意行线性变换，矩阵 AB 中对应行发生同样线性变换，d(A) 值发生同样线性变换，满足性质3；

   5）综上，d(A) 满足性质1，2，3，故 ，；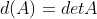

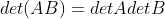10 矩阵转置后行列式不发生改变，；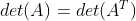

   1）假定在不需行变换下可对矩阵进行 LU 分解，；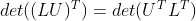

   2）利用性质9，；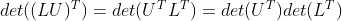

   3）由于矩阵 L 为三角矩阵，且对角元素均为1，；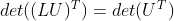

   4）由于矩阵 U 为三角矩阵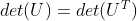，，因此，；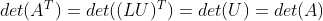

   5）在矩阵 LU 分解时引入行变换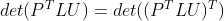，, 由于 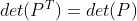，故可忽略行变换影响；

 

行列式计算

   1）以3*3矩阵为例，使用行列式线性特性，将矩阵第一行进行分解：

      ；

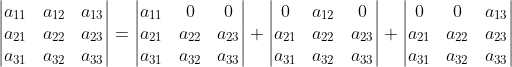  2）对分解后的三项对矩阵第二行再次分解：

     ，

     ，

     ；

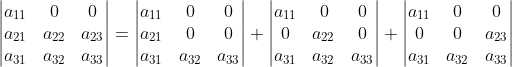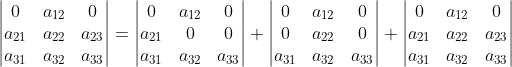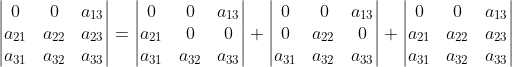  3）对分解后的九项第三行再次分解：

     ，

     ...... 

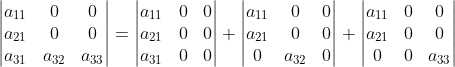  4）通过以上分解，3*3 矩阵的行列式被分解为 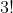 个行列式的线性组合。在 27 个行列式中，有很大一部分值为 0，仅当各行元素不再同一列时，行列式值不为0。

       通过交换矩阵行，所有矩阵可变为对角矩阵，故行列式值公式可表示为：

      ，

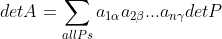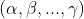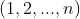     其中， 为  的全排列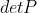， 取决于在该排列下将矩阵变为对角矩阵的行变换次数的奇偶性，

     当行变换次数为奇数时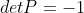，；当行变换次数为偶数时， 。

 

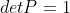 参考资料 Linear Algebra And Its Applications   Gilbert Strang