扩展欧几里德算法详解

Posted 2020-10-03

  扩展欧几里德算法

    谁是欧几里德？自己百度去

    先介绍什么叫做欧几里德算法

    有两个数 a b，现在，我们要求 a b 的最大公约数，怎么求？枚举他们的因子？不现实，当 a b 很大的时候，枚举显得那么的na?ve ，那怎么做？

    欧几里德有个十分又用的定理： gcd(a, b) = gcd(b , a%b) ，这样，我们就可以在几乎是 log 的时间复杂度里求解出来 a 和 b 的最大公约数了，这就是欧几里德算法，用 C++ 语言描述如下：

    

 

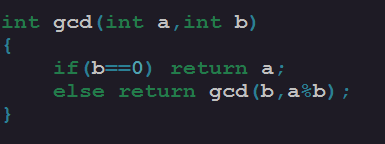
    由于是用递归写的，所以看起来很简洁，也很好记忆。那么什么是扩展欧几里德呢？

    现在我们知道了 a 和 b 的最大公约数是 gcd ，那么，我们一定能够找到这样的 x 和 y ，使得: a*x + b*y = gcd 这是一个不定方程（其实是一种丢番图方程），有多解是一定的，但是只要我们找到一组特殊的解 x0 和 y0 那么，我们就可以用 x0 和 y0 表示出整个不定方程的通解：

        x = x0 + (b/gcd)*t

        y = y0 – (a/gcd)*t

    为什么不是：

        x = x0 + b*t

        y = y0 – a*t

    这个问题也是在今天早上想通的，想通之后忍不住喷了自己一句弱逼。那是因为：

    b/gcd 是 b 的因子， a/gcd 是 a 的因子是吧？那么，由于 t的取值范围是整数，你说 (b/gcd)*t 取到的值多还是 b*t 取到的值多？同理，(a/gcd)*t 取到的值多还是 a*gcd 取到的值多？那肯定又要问了，那为什么不是更小的数，非得是 b/gcd 和a/gcd ？

    注意到：我们令 B = b/gcd ， A = a、gcd ， 那么，A 和 B 一定是互素的吧？这不就证明了 最小的系数就是 A 和 B 了吗？要是实在还有什么不明白的，看看《基础数论》（哈尔滨工业大学出版社），这本书把关于不定方程的通解讲的很清楚

    现在，我们知道了一定存在 x 和 y 使得 ： a*x + b*y = gcd ， 那么，怎么求出这个特解 x 和 y 呢？只需要在欧几里德算法的基础上加点改动就行了。

    我们观察到：欧几里德算法停止的状态是： a= gcd ， b = 0 ，那么，这是否能给我们求解 x y 提供一种思路呢？因为，这时候，只要 a = gcd 的系数是 1 ，那么只要 b 的系数是 0 或者其他值（无所谓是多少，反正任何数乘以 0 都等于 0 但是a 的系数一定要是 1），这时，我们就会有： a*1 + b*0 = gcd

    当然这是最终状态，但是我们是否可以从最终状态反推到最初的状态呢？

    假设当前我们要处理的是求出 a 和 b的最大公约数，并求出 x 和 y 使得 a*x + b*y= gcd ，而我们已经求出了下一个状态：b 和 a%b 的最大公约数，并且求出了一组x1 和y1 使得： b*x1 + (a%b)*y1 = gcd ， 那么这两个相邻的状态之间是否存在一种关系呢？

    我们知道： a%b = a - (a/b)*b（这里的 “/” 指的是整除，例如 5/2=2 , 1/3=0），那么，我们可以进一步得到：

        gcd = b*x1 + (a-(a/b)*b)*y1

            = b*x1 + a*y1 – (a/b)*b*y1

            = a*y1 + b*(x1 – a/b*y1)

    对比之前我们的状态：求一组 x 和 y 使得：a*x + b*y = gcd ，是否发现了什么？

    这里：

        x = y1

        y = x1 – a/b*y1

    以上就是扩展欧几里德算法的全部过程，依然用递归写：

    

 

    依然很简短，相比欧几里德算法，只是多加了几个语句而已。

    这就是理论部分，欧几里德算法部分我们好像只能用来求解最大公约数，但是扩展欧几里德算法就不同了，我们既可以求出最大公约数，还可以顺带求解出使得： a*x + b*y = gcd 的通解 x 和 y

    扩展欧几里德有什么用处呢？

    求解形如 a*x +b*y = c 的通解，但是一般没有谁会无聊到让你写出一串通解出来，都是让你在通解中选出一些特殊的解，比如一个数对于另一个数的乘法逆元

    什么叫乘法逆元？

    

    这里，我们称 x 是 a 关于 m 的乘法逆元

    这怎么求？可以等价于这样的表达式： a*x + m*y = 1

    看出什么来了吗？没错，当gcd(a , m) != 1 的时候是没有解的这也是 a*x + b*y = c 有解的充要条件： c % gcd(a , b) == 0

    接着乘法逆元讲，一般，我们能够找到无数组解满足条件，但是一般是让你求解出最小的那组解，怎么做？我们求解出来了一个特殊的解 x0 那么，我们用 x0 % m其实就得到了最小的解了。为什么？

可以这样思考：

    x 的通解不是 x0 + m*t 吗？

    那么，也就是说， a 关于 m 的逆元是一个关于 m 同余的，那么根据最小整数原理，一定存在一个最小的正整数，它是 a 关于m 的逆元，而最小的肯定是在（0 , m）之间的，而且只有一个，这就好解释了。

    可能有人注意到了，这里，我写通解的时候并不是 x0 + (m/gcd)*t ，但是想想一下就明白了，gcd = 1，所以写了跟没写是一样的，但是，由于问题的特殊性，有时候我们得到的特解 x0 是一个负数，还有的时候我们的 m 也是一个负数这怎么办？

    当 m 是负数的时候，我们取 m 的绝对值就行了，当 x0 是负数的时候，他模上 m 的结果仍然是负数（在计算机计算的结果上是这样的，虽然定义的时候不是这样的），这时候，我们仍然让 x0 对abs(m) 取模，然后结果再加上abs(m) 就行了，于是，我们不难写出下面的代码求解一个数 a 对于另一个数 m 的乘法逆元：

    

 

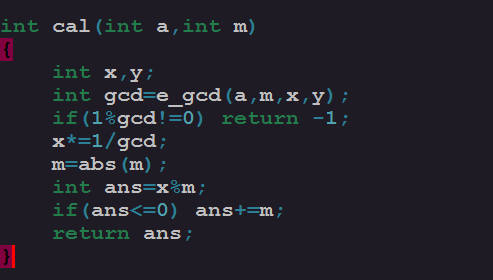
    还有最小整数解之类的问题，但都是大同小异，只要细心的推一推就出来了，这里就不一一介绍了，下面给一些题目还有AC代码，仅供参考

    ZOJ 3609 ：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=4712 求最小逆元

    

[cpp] view plain copy

 

1. #include <iostream>  
2. #include <cstdio>  
3. #include <cstring>  
4. #include <cmath>  
5. #include <vector>  
6. #include <string>  
7. #include <queue>  
8. #include <stack>  
9. #include <algorithm>  
10.   
11. #define INF 0x7fffffff  
12. #define EPS 1e-12  
13. #define MOD 1000000007  
14. #define PI 3.141592653579798  
15. #define N 100000  
16.   
17. using namespace std;  
18.   
19. typedef long long LL;  
20. typedef double DB;  
21.   
22. LL e_gcd(LL a,LL b,LL &x,LL &y)  
23. {  
24.     if(b==0)  
25.     {  
26.         x=1;  
27.         y=0;  
28.         return a;  
29.     }  
30.     LL ans=e_gcd(b,a%b,x,y);  
31.     LL temp=x;  
32.     x=y;  
33.     y=temp-a/b*y;  
34.     return ans;  
35. }  
36.   
37. LL cal(LL a,LL b,LL c)  
38. {  
39.     LL x,y;  
40.     LL gcd=e_gcd(a,b,x,y);  
41.     if(c%gcd!=0) return -1;  
42.     x*=c/gcd;  
43.     b/=gcd;  
44.     if(b<0) b=-b;  
45.     LL ans=x%b;  
46.     if(ans<=0) ans+=b;  
47.     return ans;  
48. }  
49.   
50. int main()  
51. {  
52.     LL a,b,t;  
53.     scanf("%lld",&t);  
54.     while(t--)  
55.     {  
56.         scanf("%lld%lld",&a,&b);  
57.         LL ans=cal(a,b,1);  
58.         if(ans==-1) printf("Not Exist\n");  
59.         else printf("%lld\n",ans);  
60.     }  
61.     return 0;  
62. }  

ZOJ 3593 http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3593 求最小的步数，处理特殊一点就过去了

 

 

[cpp] view plain copy

 

1. #include <iostream>  
2. #include <cstdio>  
3. #include <cstring>  
4. #include <cmath>  
5. #include <string>  
6. #include <vector>  
7. #include <stack>  
8. #include <queue>  
9. #include <algorithm>  
10.   
11. #define INF 0x7fffffff  
12. #define EPS 1e-12  
13. #define MOD 100000007  
14. #define PI 3.14159265357979823846  
15. #define N 100005  
16.   
17. using namespace std;  
18.   
19. typedef long long LL;  
20.   
21. LL e_gcd(LL a,LL b,LL &x,LL &y)  
22. {  
23.     if(b==0)  
24.     {  
25.         x=1;  
26.         y=0;  
27.         return a;  
28.     }  
29.     LL ans=e_gcd(b,a%b,x,y);  
30.     LL temp=x;  
31.     x=y;  
32.     y=temp-a/b*y;  
33.     return ans;  
34. }  
35. LL cal(LL a,LL b,LL L)  
36. {  
37.     LL x,y;  
38.     LL gcd=e_gcd(a,b,x,y);  
39.     if(L%gcd!=0) return -1;  
40.     x*=L/gcd;  
41.     y*=L/gcd;  
42.     a/=gcd;  
43.     b/=gcd;  
44.     LL ans=((LL)INF)*((LL)INF), f;  
45.     LL mid=(y-x)/(a+b);  
46.     for(LL T=mid-1;T<=mid+1;T++)  
47.     {  
48.         if(abs(x+b*T)+abs(y-a*T)==abs(x+b*T+y-a*T))  
49.             f=max(abs(x+b*T),abs(y-a*T));  
50.         else  
51.             f=fabs(x-y+(a+b)*T);  
52.         ans=min(ans,f);  
53.     }  
54.     return ans;  
55. }  
56.   
57. int main()  
58. {  
59.     //freopen("in.in","r",stdin);  
60.     //freopen("out.out","w",stdout);  
61.     LL A,B,a,b,x,y;  
62.     int t; scanf("%d",&t);  
63.     while(t--)  
64.     {  
65.         scanf("%lld%lld%lld%lld",&A,&B,&a,&b);  
66.         LL L=B-A;  
67.         LL ans=cal(a,b,L);  
68.         if(ans==-1) printf("-1\n");  
69.         else printf("%lld\n",ans);  
70.     }  
71.     return 0;  
72. }  

POJ 1061 http://poj.org/problem?id=1061 青蛙的约会，裸的扩展欧几里得

 

 

[cpp] view plain copy

 

1. #include <iostream>  
2. #include <cstdio>  
3. #include <cstring>  
4. #include <cmath>  
5. #include <vector>  
6. #include <string>  
7. #include <queue>  
8. #include <stack>  
9. #include <algorithm>  
10.   
11. #define INF 0x7fffffff  
12. #define EPS 1e-12  
13. #define MOD 1000000007  
14. #define PI 3.141592653579798  
15. #define N 100000  
16.   
17. using namespace std;  
18.   
19. typedef long long LL;  
20. typedef double DB;  
21.   
22. LL e_gcd(LL a,LL b,LL &x,LL &y)  
23. {  
24.     if(b==0)  
25.     {  
26.         x=1;  
27.         y=0;  
28.         return a;  
29.     }  
30.     LL ans=e_gcd(b,a%b,x,y);  
31.     LL temp=x;  
32.     x=y;  
33.     y=temp-a/b*y;  
34.     return ans;  
35. }  
36.   
37. LL cal(LL a,LL b,LL c)  
38. {  
39.     LL x,y;  
40.     LL gcd=e_gcd(a,b,x,y);  
41.     if(c%gcd!=0) return -1;  
42.     x*=c/gcd;  
43.     b/=gcd;  
44.     if(b<0) b=-b;  
45.     LL ans=x%b;  
46.     if(ans<=0) ans+=b;  
47.     return ans;  
48. }  
49.   
50. int main()  
51. {  
52.     LL x,y,m,n,L;  
53.     while(scanf("%lld%lld%lld%lld%lld",&x,&y,&m,&n,&L)!=EOF)  
54.     {  
55.         LL ans=cal(m-n,L,y-x);  
56.         if(ans==-1) printf("Impossible\n");  
57.         else printf("%lld\n",ans);  
58.     }  
59.     return 0;  
60. }  

HDU 1576 http://acm.hdu.edu.cn/showproblem.php?pid=1576 做点处理即可

 

 

[cpp] view plain copy

 

1. #include <iostream>  
2. #include <cstdio>  
3. #include <cstring>  
4. #include <cmath>  
5. #include <vector>  
6. #include <string>  
7. #include <queue>  
8. #include <stack>  
9. #include <algorithm>  
10.   
11. #define INF 0x7fffffff  
12. #define EPS 1e-12  
13. #define MOD 1000000007  
14. #define PI 3.141592653579798  
15. #define N 100000  
16.   
17. using namespace std;  
18.   
19. typedef long long LL;  
20. typedef double DB;  
21.   
22. LL e_gcd(LL a,LL b,LL &x,LL &y)  
23. {  
24.     if(b==0)  
25.     {  
26.         x=1;  
27.         y=0;  
28.         return a;  
29.     }  
30.     LL ans=e_gcd(b,a%b,x,y);  
31.     LL temp=x;  
32.     x=y;  
33.     y=temp-a/b*y;  
34.     return ans;  
35. }  
36.   
37. LL cal(LL a,LL b,LL c)  
38. {  
39.     LL x,y;  
40.     LL gcd=e_gcd(a,b,x,y);  
41.     if(c%gcd!=0) return -1;  
42.     x*=c/gcd;  
43.     b/=gcd;  
44.     if(b<0) b=-b;  
45.     LL ans=x%b;  
46.     if(ans<=0) ans+=b;  
47.     return ans;  
48. }  
49.   
50. int main()  
51. {  
52.     LL n,b,t;  
53.     scanf("%I64d",&t);  
54.     while(t--)  
55.     {  
56.         scanf("%I64d%I64d",&n,&b);  
57.         LL ans=cal(b,9973,n);  
58.         if(ans==-1) printf("Impossible\n");  
59.         else printf("%lld\n",ans);  
60.     }  
61.     return 0;  
62. }  

HDU 2669 http://acm.hdu.edu.cn/showproblem.php?pid=2669 裸的扩展欧几里得

 

 

[cpp] view plain copy

 

1. #include <iostream>  
2. #include <cstdio>  
3. #include <cstring>  
4. #include <cmath>  
5. #include <vector>  
6. #include <string>  
7. #include <queue>  
8. #include <stack>  
9. #include <algorithm>  
10.   
11. #define INF 0x7fffffff  
12. #define EPS 1e-12  
13. #define MOD 1000000007  
14. #define PI 3.141592653579798  
15. #define N 100000  
16.   
17. using namespace std;  
18.   
19. typedef long long LL;  
20. typedef double DB;  
21.   
22. LL e_gcd(LL a,LL b,LL &x,LL &y)  
23. {  
24.     if(b==0)  
25.     {  
26.         x=1;  
27.         y=0;  
28.         return a;  
29.     }  
30.     LL ans=e_gcd(b,a%b,x,y);  
31.     LL temp=x;  
32.     x=y;  
33.     y=temp-a/b*y;  
34.     return ans;  
35. }  
36.   
37. LL cal(LL a,LL b,LL c)  
38. {  
39.     LL x,y;  
40.     LL gcd=e_gcd(a,b,x,y);  
41.     if(c%gcd!=0) return -1;  
42.     x*=c/gcd;  
43.     b/=gcd;  
44.     if(b<0) b=-b;  
45.     LL ans=x%b;  
46.     if(ans<=0) ans+=b;  
47.     return ans;  
48. }  
49.   
50. int main()  
51. {  
52.     LL a,b;  
53.     while(scanf("%I64d%I64d",&a,&b)!=EOF)  
54.     {  
55.         LL ans=cal(a,b,1);  
56.         if(ans==-1) printf("sorry\n");  
57.         else printf("%I64d %I64d\n",ans,(1-ans*a)/b);  
58.     }  
59.     return 0;  
60. }  

暂时就这么多了吧