ACwing（基础）--- Dijkstra算法（含堆优化版）

Posted 2020-12-14 bingers

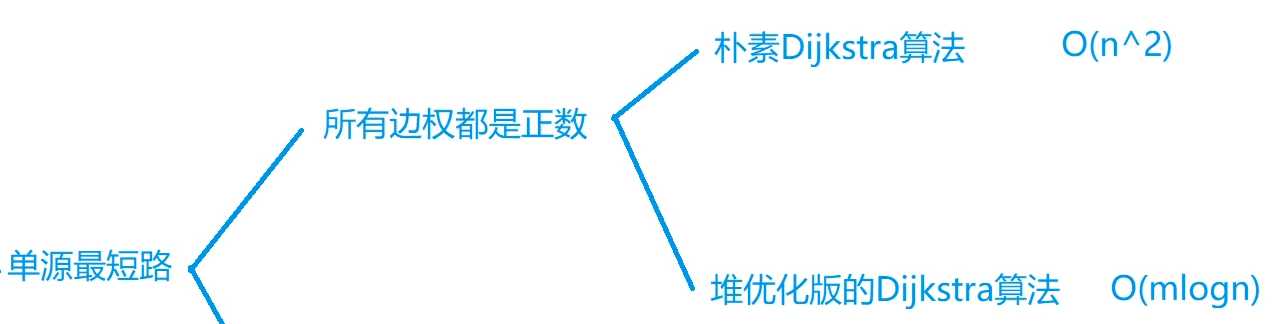
朴素Dijkstra算法

• 时间复杂是 O(n^2+m), n 表示点数，m 表示边数
• 适合稠密图

#include<cstring>
#include<iostream>
#include<algorithm>
#define mm(a,x) memset(a,x,sizeof(a))
#define inf 0x3f3f3f3f
using namespace std;

const int maxn = 510;

int n,m;
int mp[maxn][maxn];
int dist[maxn];
int vis[maxn];

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra(){
    mm(dist,0x3f);//初始化距离  0x3f代表无限大
    dist[1]=0;//第一个点到自身的距离为0
    for(int i=0;i<n;i++){
        int t=-1; // 在还未确定最短路的点中，寻找距离最小的点
        for(int j=1;j<=n;j++)//从一号点开始
            if(!vis[j]&&(t==-1||dist[t]>dist[j]))
            t=j;
        vis[t]=1;
        // 用t更新其他点的距离
        for(int j=1;j<=n;j++)
            dist[j]=min(dist[j],dist[t]+mp[t][j]);
    }
    if(dist[n]==inf) return -1;//如果第n个点路径为无穷大即不存在最低路径
    return dist[n];
}

int main(){
    cin>>n>>m;
    mm(mp,0x3f);
    while(m--){
        int a,b,c;
        cin>>a>>b>>c;
        mp[a][b]=min(mp[a][b],c);
    }
    int t=dijkstra();
    cout<<t;
    return 0;
}

堆优化版Dijkstra

• 时间复杂度为O（mlogn），n表示点数，m表示边数
• 堆优化版的dijkstra是对朴素版dijkstra进行了优化
• 在朴素版dijkstra中时间复杂度最高的寻找距离最短的点O(n^2)可以使用最小堆优化。

1. 一号点的距离初始化为零，其他点初始化成无穷大。
2. 将一号点放入堆中。
3. 不断循环，直到堆空。每一次循环中执行的操作为：
   弹出堆顶（与朴素版diijkstra找到S外距离最短的点相同，并标记该点的最短路径已经确定）。
   用该点更新临界点的距离，若更新成功就加入到堆中。

时间复杂度分析

寻找路径最短的点：O(n)

加入集合S：O(n)

更新距离：O(mlogn)

#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
#define mm(a,x) memset(a,x,sizeof a)
#define inf 0x3f3f3f3f
using namespace std;

typedef pair<int ,int > PII;
const int maxn = 1e6+10;

int n,m;
int h[maxn],w[maxn],e[maxn],ne[maxn],idx;
int dist[maxn],vis[maxn];

void add(int a,int b,int c) {
	e[idx] =b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

int dijkstra() {
	mm(dist,inf);
	dist[1]=0;
	priority_queue<PII,vector<PII>,greater<PII>> heap; // 定义一个小根堆
	heap.push({0,1});// 这个顺序不能倒，pair排序时是先根据first，再根据second，这里显然要根据距离排序
	while(heap.size()) {
		auto t =heap.top();// 取不在集合S中距离最短的点
		heap.pop();
		int ver=t.second,distance = t.first;
		if(vis[ver]) continue;
		vis[ver]=1;//标记该点
		for(int i = h[ver];i!=-1;i = ne[i]){
			int j = e[i];// i只是个下标，e中在存的是i这个下标对应的点
			if(dist[j] > distance + w[i]){
				dist[j] = distance + w[i];
				heap.push({dist[j],j});//放入堆中，更新其他点
			}
		}
	}
	
	if(dist[n] == inf) return -1;
	return dist[n];
}

int main() {
	scanf("%d%d",&n,&m);
	mm(h,-1);
	while(m--){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
	}
	int t=dijkstra();
	printf("%d
",t);
	return 0;
}