dp-状压dp

Posted 2020-12-13 aliencxl

https://www.bilibili.com/video/BV1Z4411x7Kw?from=search&seid=13855865082722302053

状压介绍：

状态表示：

 

 转移方程：i是当前节点，j是下一步要走的节点

 

 子集枚举：

核心代码：1。由当前枚举未知

首先枚举状态，枚举S中包含的节点：枚举i能去的节点

 

 2.由已知枚举当前

枚举状态S：S ^ (1 << i) 表示去掉i节点

5435. 并行课程 II

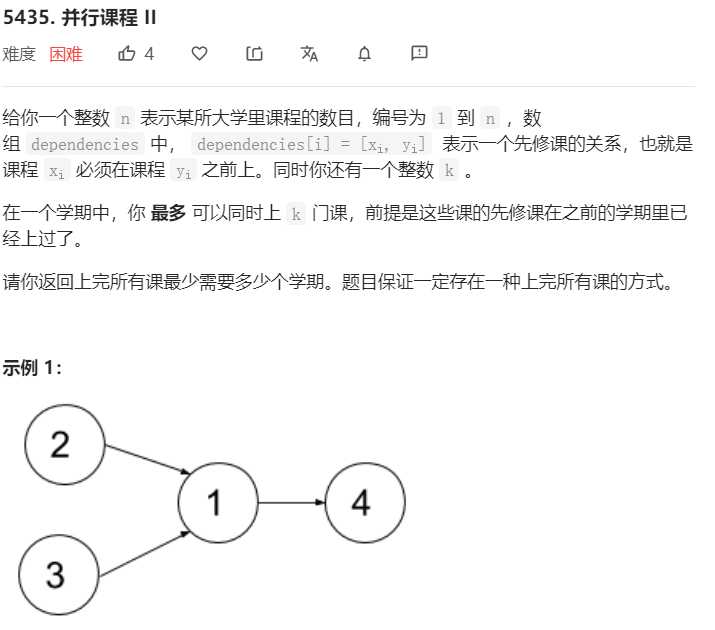
yxc代码

 const int INF = 1000;
    vector<int> f;

    int minNumberOfSemesters(int n, vector<vector<int>>& edges, int k) {
        f = vector<int>(1 << n, INF);//dp数组
        for (auto& e: edges) e[0] --, e[1] -- ;
        f[0] = 0;// 还没选任何课
        for (int i = 0; i < 1 << n; i ++ ) {//遍历所有状态
            vector<bool> st(n);// 求当前可以选的课有哪些
            for (auto& e: edges) {
                int x = e[0], y = e[1];
                if (!(i >> x & 1)) //如果x没有修过
                    st[y] = true;//y有些先修课没被修过
            }
            int state = 0;//state的二进制位表示可以修的课程
            for (int j = 0; j < n; j ++ )
                if (!st[j] && !(i >> j & 1))// j所有先修课修过，并且j还没有被修
                    state += 1 << j;//则修课程j
            
            dfs(n, k, i, state, 0,0);//i的状态转移
        }

        return f[(1 << n) - 1];//返回全部修过时的最短
    }
    //state中选出k个元素来更新
    void dfs(int n, int k, int i, int state, int now, int start) {
        //参数 i 是当前状态，state是可以选的状态, now 是当前已选的状态, start是开始选的元素，避免重复计算
        if (!k || !state) {//选了k个课，或者没课可选
            f[i | now] = min(f[i | now], f[i] + 1);
            return;
        }
        //当前可以选那些课
        for (int j = start; j < n; j ++ ) {
            if (state >> j & 1) {//如果state中包含这些课
                dfs(n, k - 1, i, state - (1 << j), now + (1 << j), j + 1);
                //state去掉当前选的课， now加上当前选的课
            }
        }
    }

HUD 5148

http://acm.hdu.edu.cn/showproblem.php?pid=5418

递推：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 17;
const int INF = 0x3f3f3f3f;
int n, m, g[maxn][maxn], dp[1<<maxn][maxn];
 
void floyd()
{
    for(int k = 0; k < n; k++)
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++)
                g[i][j] = min(g[i][j], g[i][k]+g[k][j]);
}
 
int main(void)
{
    int t;
    cin >> t;
    while(t--)
    {
        scanf("%d%d", &n, &m);
        //对图进行初始化
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++)
                g[i][j] = i==j ? 0 : INF;
        //插入边
        while(m--)
        {
            int u, v, w;
            scanf("%d%d%d", &u, &v, &w);
            u--, v--;
            g[u][v] = min(g[u][v], w);
            g[v][u] = min(g[v][u], w);
        }
        //floyd算法
        floyd();
        memset(dp, INF, sizeof(dp));
        dp[0][0] = 0;
        for(int s = 0; s < 1<<n; s++)//遍历所有状态
            for(int v = 0; v < n; v++)//遍历所有节点
                if(dp[s][v] != INF) 
                    for(int u = 0; u < n; u++)
                        dp[s|(1<<u)][u] = min(dp[s|(1<<u)][u], dp[s][v]+g[v][u]);
        printf("%d
", dp[(1<<n)-1][0]);
    }
    return 0;
}

递归：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn = 17;
const int INF = 0x3f3f3f3f;
int dp[1<<maxn][maxn], g[maxn][maxn], n, m;
 
void floyd()
{
    for(int k = 0; k < n; k++)
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++)
                g[i][j] = min(g[i][j], g[i][k]+g[k][j]);
}
 
int dfs(int S, int v)
{
    if(dp[S][v] >= 0) return dp[S][v]; // 状态已经遍历过
    if(S == (1<<n)-1 && v == 0) return dp[S][v] = 0;//回到终点
    int res = INF;
    for(int u = 0; u < n; u++)
    {
        if(!(S>>u & 1))//当前还没遍历过u节点，则遍历u节点
            res = min(res, dfs(S | 1<<u, u)+g[v][u]);
    }
    return dp[S][v] = res;
}
 
int main(void)
{
    int t;
    cin >> t;
    while(t--)
    {
        scanf("%d%d", &n, &m);
        //将图初始化
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++)
                g[i][j] = i==j ? 0 : INF;
        //加入边
        while(m--)
        {
            int u, v, w;
            scanf("%d%d%d", &u, &v, &w);
            u--, v--;
            g[u][v] = min(g[u][v], w);
            g[v][u] = min(g[v][u], w);
        }
        //因为有些节点不是直接相连，进行floyd算法
        floyd();
        //dp 数组初始化
        memset(dp, -1, sizeof(dp));
        //dfs遍历
        printf("%d
", dfs(0, 0));
    }
    return 0;
}