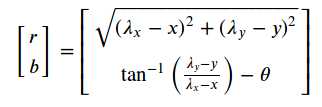图优化

Posted 2020-12-12 yrm1160029237

1.图优化的流程

1. 选择你想要的图里的节点与边的类型，确定它们的参数化形式；
2. 往图里加入实际的节点和边；
3. 选择初值，开始迭代；
4. 每一步迭代中，计算对应于当前估计值的雅可比矩阵和海塞矩阵；
5. 求解稀疏线性方程 H * detaX = -b，得到梯度方向；
6. 继续用GN或LM进行迭代。如果迭代结束，返回优化值。

　　实际上，g2o能帮你做好第3-6步，你要做的只是前两步而已。

 

2.顶点和边

• 在图中，以顶点表示优化变量，以边表示观测方程。

	两个顶点	一条边边
机器人两个Pose之间的变换	两个pose	变换关系： detaT = T1 * inv(T2)
机器人在某个Pose处用激光测量到了某个空间点	一个2D Pose[x,y,theta]; 一个空间点(lamda_x，lamda_y)	观测方程：
机器人在某个Pose处用相机观测到了某个空间点，得到了它的像素坐标	一个像素坐标 Pose = [u; v] 一个空间点x = (x,y,z)	z = [u; v] = C (R * x + t)， C为相机内参

•  优化目标

 

 

 

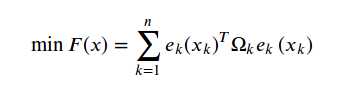
e(x,k) 是x符合z的程度的一个度量，越小越符合，反之越不符合。对式进行求导和一阶泰勒展开，得到其极值为0的方程：

 

 

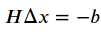
 其中，deta X即为梯度。

• 可解性解释

 

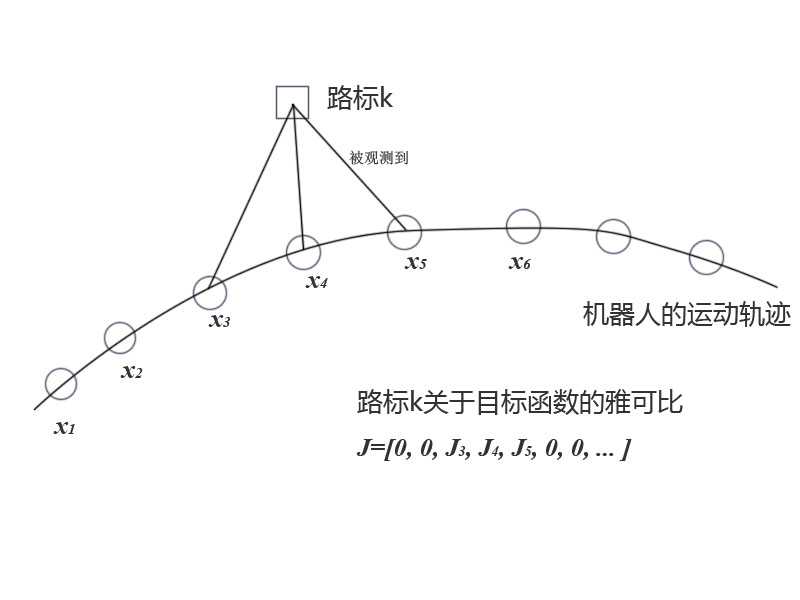
 只有和xk顶点相连的边，出现了非零值。相应的二阶导矩阵H中，大部分也是零元素。这种稀疏性能很好地帮助我们快速求解上面的线性方程。稀疏矩阵代数库：SBA、PCG、CSparse、Cholmod等等

•  引入核函数的原因，是因为SLAM中可能给出错误的边。如cauchy核，huber核等等。
• 问题： 四维变换矩阵T或者三维旋转矩R无法进行加减和求导：李群和李代数变换后可以，再变换回来。

 

2.g2o库

 

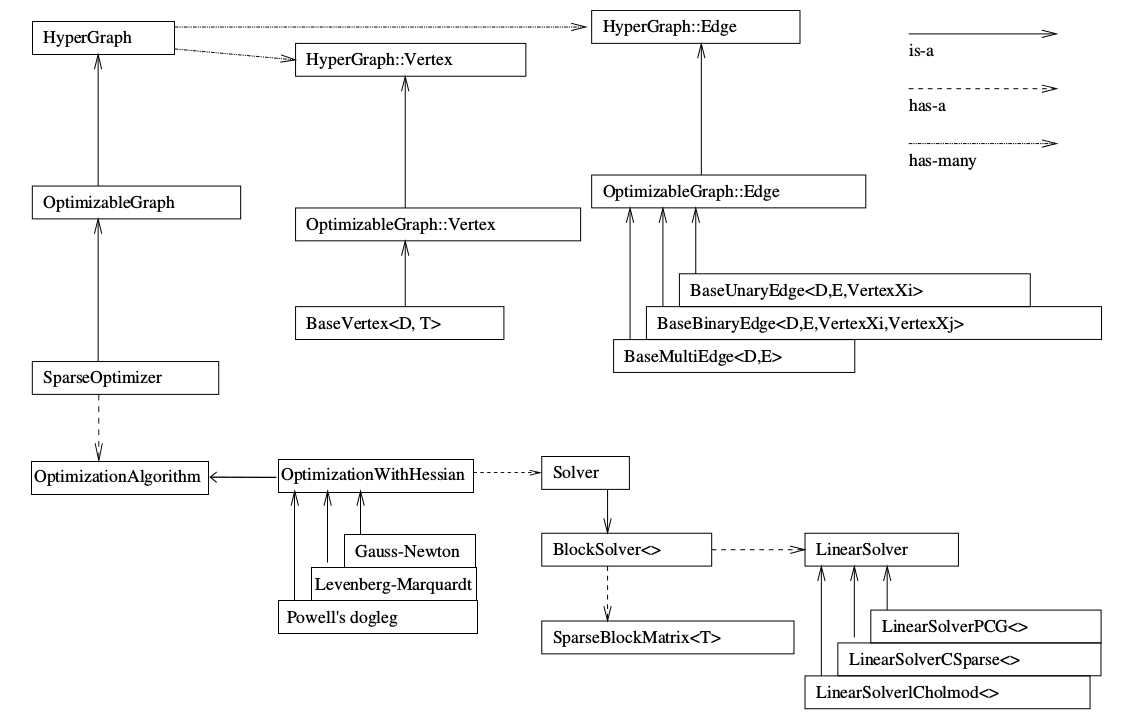
 3.应用

参考：https://www.cnblogs.com/gaoxiang12/p/5304272.html

 

1. 定义顶点
2. 定义边
3. 配置BlockSolver(LinerSolverType)
4. 配置OptimizationAlgorithm
5. 配置Optimizer
6. 添加顶点
7. 添加边
8. 启动优化

 

 

总结：

重要参考：https://www.cnblogs.com/gaoxiang12/p/5244828.html

https://www.aiimooc.com/mall/preshow-htm-itemid-382.html