B Hat(线段树 - Lazy标记区间查询)

Posted 2020-12-11 zut-syp

链接：https://namomo.top:8081/contest/1/problem/B
来源：Namomo Test Round 1

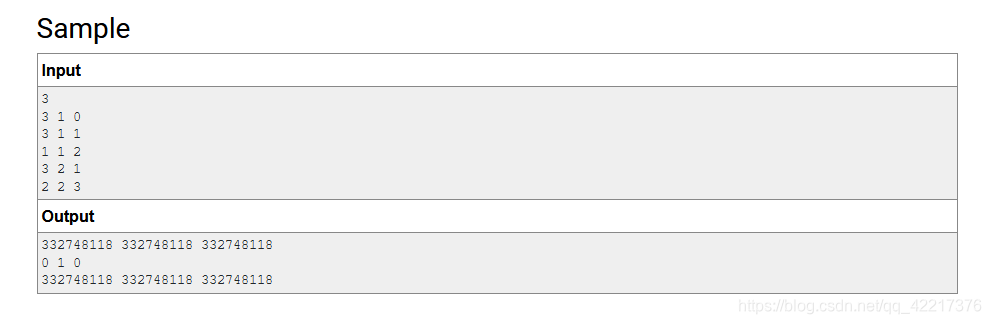
??思路：首先设第 (i) 个位置的概率为 (p_{i})，刚开始的时候 (p_{1} = 1)，其他的都是 (0)。当一个操作能够被看到的时候，如果交换两个位置，那么两个位置有兔子的概率将会被交换，也就是交换两个 (p) 值，即 (swap(p_{i}, p_{j}))。当一个操作不能够被看到的时候，此时就分为两种情况，第一种是当前的帽子不会被选中，当前帽子不被选中的概率为

??????????????????????(frac{C_{n-1}^{2}}{C_{n}^{2}} = frac{(n - 1) × (n - 2)}{n × (n - 1)} = frac{n - 2}{n})

那么当前位置有兔子的概率为 (frac{(n - 2)}{n} × p)，另外一种情况就是当前的帽子被选中，按照上述条件可以知道被选中的概率为 (frac{2}{n})，如果最终想要这个帽子有兔子，那么选择的另外一个帽子中必定有兔子，这样才能保证交换以后当前帽子中有兔子，我们要在剩下 (n - 1) 个帽子中选择一个有兔子的帽子，另外一个帽子有兔子的概率为

?????? (sum_{j = 1}^{n} frac{1}{n-1} × p_{j} - frac{1}{n-1} × p_{i} = frac{1}{n-1} × (sum_{j = 1}^{n} p_{j} - p_{i}) = frac{1}{n - 1} × (1 - p_{i}) = frac{1}{n - 1} × (1 - p))

那么在这种情况下当前帽子中有兔子的概率为 (frac{2}{n} × frac{1}{n - 1} × (1 - p))

综上所述，当前帽子下有兔子的概率为

????(frac{n - 2}{n} × p) + (frac{2}{n} × frac{1}{n - 1} × (1 - p) = frac{n - 2}{n} × p + frac{2}{n(n - 1)} - frac{2}{n(n - 1)} × p = frac{2}{n(n - 1)} + ( frac{n - 2}{n} - frac{2}{n(n - 1)}) × p)

我们在进行修改概率的时候，对于每一个帽子都需要进行修改，所以使用线段树进行区间的修改，当是已知操作数进行概率交换的时候我们对线段树的叶结点进行单点修改，线段树中维护两个值，一个是要乘的数 (k)，另外一个是要加的数 (b)，当我们在修改的时候可以下传到某一个位置，如果满足条件就不在进行下传，保存当前的结点信息，在查询的时候如果需要下传就将信息下传并且更新当前结点的信息，直到下传到我的想要的值，在修改的时候，当往上传的时候说明此时需要更新的点已经更新完毕，我们需要把每个结点的信息要乘上的数变为 (1)，要加上的数变成 (0)。

#include<bits/stdc++.h>
using namespace std;
#define LNode x << 1
#define RNode x << 1 | 1

typedef long long ll;
const int maxn = 1e5 + 10;
const int mod = 998244353;
int x[maxn], y[maxn];
bool flag[maxn];

struct tree {
	ll k, b, sum;
	/*tree operator + (const tree & xxx) const {
		tree ans;
		ans.k = 1, ans.b = 0;
		ans.sum = (sum + xxx.sum) % mod;
		return ans;
	}*/
}tree[maxn << 2];

ll quickPow(ll a, ll b) {
	ll ans = 1, res = a;
	while(b) {
		if(b & 1) ans = ans * res % mod;
		res = res * res % mod;
		b >>= 1;
	}
	return ans % mod;
}

ll inv(ll x) {
	return quickPow(x % mod, mod - 2);
}

void pushUp(int x) {
	//tree[x] = tree[LNode] + tree[RNode];
	tree[x].k = 1; tree[x].b = 0;
}

void pushDown(int x, ll k, ll b) {
	tree[LNode].k = tree[LNode].k * k % mod;
	tree[LNode].b = (tree[LNode].b * k % mod + b) % mod;
	tree[LNode].sum = (tree[LNode].sum * k % mod + b) % mod;
	tree[RNode].k = tree[RNode].k * k % mod;
	tree[RNode].b = (tree[RNode].b * k % mod + b) % mod;
	tree[RNode].sum = (tree[RNode].sum * k % mod + b) % mod;
	tree[x].k = 1; tree[x].b = 0;
}

void build(int l, int r, int x) {
	if(l == r) {
		tree[x].sum = 0;
		tree[x].k = 1;
		tree[x].b = 0;
		return ;
	}
	int mid = (l + r) >> 1;
	build(l, mid, LNode);
	build(mid+1, r, RNode);
	pushUp(x);
}
//单点修改
void modify(int l, int r, int x, int pos, int val) {
	if(l == r) {
		tree[x].sum = val;
		return ;
	}
	pushDown(x, tree[x].k, tree[x].b);
	int mid = (l + r) >> 1;
	if(pos <= mid) modify(l, mid, LNode, pos, val);
	else modify(mid+1, r, RNode, pos, val);
	pushUp(x);
}
//区间查询
/*
int query(int l, int r, int L, int R, int x) {
	if(L <= l && R >= r) return sum[x];
	pushDown(x);
	int mid = (l + r) >> 1, ans = 0;
	if(L <= mid) ans += query(l, mid, L, R, x);
	else ans += query(mid+1, r, L, R, x);
	return ans;
} */
//单点查询
int query(int l, int r, int pos, int x) {
	if(l == r) return tree[x].sum;
	pushDown(x, tree[x].k, tree[x].b);
	int mid = (l + r) >> 1;
	if(pos <= mid) return query(l, mid, pos, LNode);
	else return query(mid+1, r, pos, RNode);
}
//区间修改
void update(int l, int r, int L, int R, int x, ll k, ll b) {
	if(L <= l && R >= r) {
		tree[x].k = tree[x].k * k % mod;
		tree[x].b = (tree[x].b * k % mod+ b) % mod;
		tree[x].sum = (tree[x].sum * k % mod + b) % mod;
		return ;
	}
	pushDown(x, k, b);
	int mid = (l + r) >> 1;
	if(L <= mid) update(l, mid, L, R, LNode, k, b);
	else update(mid+1, r, L, R, RNode, k, b);
	pushUp(x);
}

int main() {
	int T; scanf("%d", &T);
	while(T --) {
		int n, m, k; scanf("%d %d %d", &n, &m, &k);
		build(1, n, 1); modify(1, n, 1, 1, 1);
		for(int i = 1; i <= m; ++i) flag[i] = false;
		for(int i = 1; i <= k; ++i) {
			int op, a, b; scanf("%d %d %d", &op, &a, &b);
			flag[op] = true; x[op] = a; y[op] = b;
		}
		for(int i = 1; i <= m; ++i) {
			if(flag[i]) {//交换
				int val1 = query(1, n, x[i], 1);
				int val2 = query(1, n, y[i], 1);
				modify(1, n, 1, x[i], val2);
				modify(1, n, 1, y[i], val1);
			} else {//计算
				ll k = (n - 2) * inv(n) - 2 * inv(1ll * n * (n - 1));
				k = (k % mod + mod) % mod;
				ll b = 2 * inv(1ll * n * (n - 1));
				b = (b % mod + mod) % mod;
				update(1, n, 1, n, 1, k, b);
			}
		}
		for(int i = 1; i <= n; ++i) printf("%d%c", query(1, n, i, 1), i == n? ‘
‘ : ‘ ‘);
	}
	return 0;
}