[P4389] 付公主的背包 - 生成函数,多项式,NTT

Posted 2020-12-10 mollnn

Description

有 (n) 种商品，每种商品体积为 (v_i)，都有无限件，给定 (m)，对于 (sin [1,m])，回答用这些商品恰好装 (s) 体积的方案数

Solution

很自然地写成形式幂级数，然后进行一通推导，如下

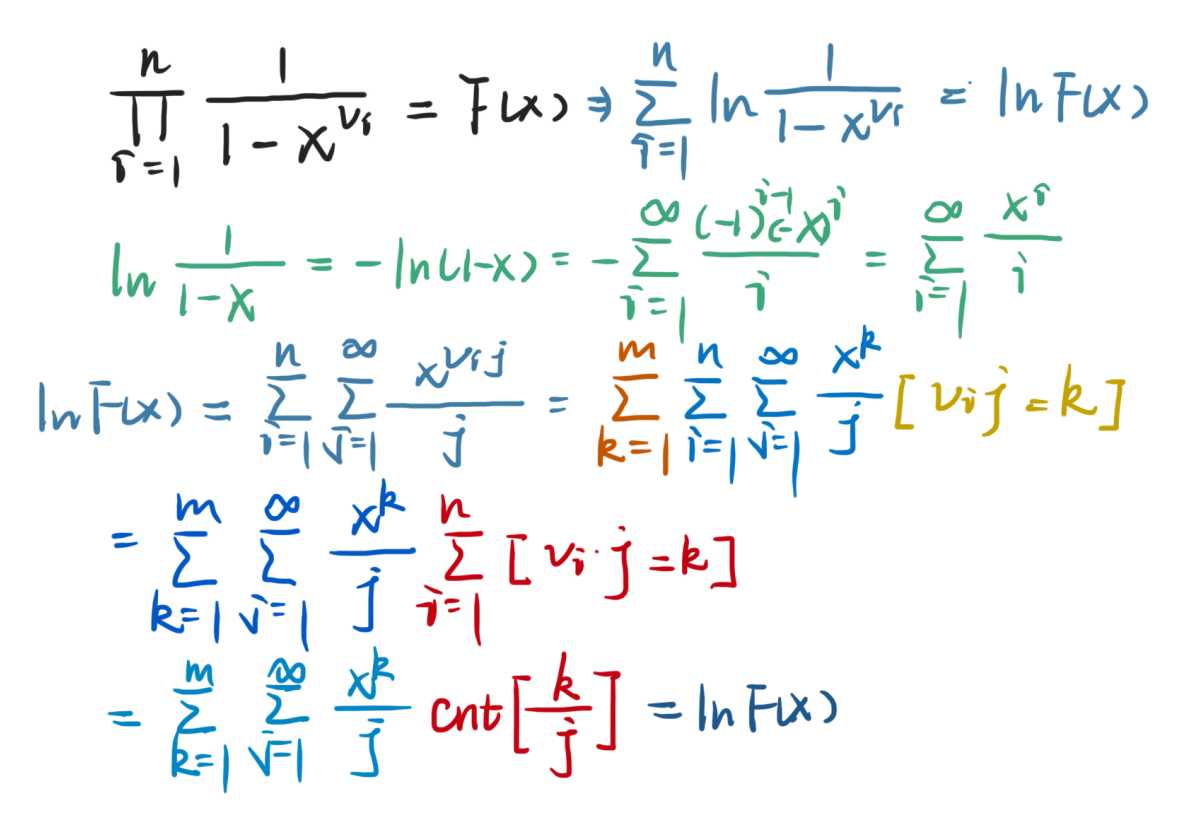
最后得到的左式可以在 (O(nsqrt n)) 时间内计算出，然后做一次多项式 exp 得到 (F)

#include <bits/stdc++.h>
using namespace std;

#define int long long
const int N = 262150;
const int mod = 998244353;

int qpow(int p,int q) {return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
int inv(int p) {return qpow(p,mod-2);}

namespace cipolla {
inline int le(int x) {return qpow(x,(mod-1)/2);}
int w;
struct comp {
    int x,y;
    comp(int a=0,int b=0) {x=a;y=b;}
};
comp operator + (comp a,comp b) {return comp((a.x+b.x)%mod,(a.y+b.y)%mod);}
comp operator - (comp a,comp b) {return comp((a.x-b.x+mod)%mod,(a.y-b.y+mod)%mod);}
comp operator * (comp a,comp b) {return comp((a.x*b.x+a.y*b.y%mod*w)%mod,(a.x*b.y+a.y*b.x)%mod);}
comp operator ^ (comp a,int b) {comp o(1,0); for(;b;a=a*a,b>>=1) if(b&1) o=o*a; return o;}
int calc(int x) {
    x%=mod;
    int a;
    while(true) {
        a=rand();
        w=(a*a-x+mod)%mod;
        if(le(w)==mod-1) break;
    }
    comp s=comp(a,1)^((mod+1)/2);
    return min(s.x,mod-s.x);
}
}

namespace po {
int rev[N],inv[N],w[N],sz;
void presolve(int l) {
    int len=1;
    sz=0;
    while(len<l) len<<=1, ++sz;
    for(int i=1;i<len;i++) {
        inv[i]=(i==1?1:inv[mod%i]*(mod-mod/i)%mod);
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(sz-1));
    }
    int wn=qpow(3,(mod-1)/len);
    w[len/2]=1;
    for(int i=len/2+1;i<len;i++) w[i]=w[i-1]*wn%mod;
    for(int i=len/2-1;i;i--) w[i]=w[i<<1];
}
int pre(int l) {int g; for(g=1;g<l;g<<=1); return g;}
void ntt(int *a,int o,int n) {
    static unsigned long long s[N];
    int t=sz-__builtin_ctz(n),x;
    for(int i=0;i<n;i++) s[rev[i]>>t]=a[i];
    for(int l=1;l<n;l<<=1) for(int i=0;i<n;i+=l<<1) for(int j=0;j<l;j++) {
        x=s[i+j+l]*w[j+l]%mod;
        s[i+j+l]=s[i+j]+mod-x;
        s[i+j]+=x;
    }
    for(int i=0;i<n;i++) a[i]=s[i]%mod;
    if(o) {
        x=qpow(n,mod-2);
        for(int i=0;i<n;i++) a[i]=a[i]*x%mod;
        reverse(a+1,a+n);
    }
}
void mult(int n,int *x,int *y,int *z) {
    static int a[N],b[N];
    int l=pre(n<<1);
    for(int i=0;i<l;i++) {
        a[i]=(i<n?x[i]:0);
        b[i]=(i<n?y[i]:0);
    }
    ntt(a,0,l); ntt(b,0,l);
    for(int i=0;i<l;i++) z[i]=a[i]*b[i]%mod;
    ntt(z,1,l);
    for(int i=n;i<l;i++) z[i]=0;
}
void inve(int len,int *a,int *b) {
    if(len==1) *b=qpow(*a,mod-2);
    else {
        inve((len+1)/2,a,b);
        static int c[N];
        int n=pre(len<<1);
        for(int i=0;i<n;i++) i<len?c[i]=a[i]:b[i]=c[i]=0;
        ntt(b,0,n);
        ntt(c,0,n);
        for(int i=0;i<n;i++) b[i]=((b[i]+b[i]-b[i]*b[i]%mod*c[i])%mod+mod)%mod;
        ntt(b,1,n);
        for(int i=len;i<n;i++) b[i]=0;
    }
}
void sqrt(int n,int *a,int *b) {
    if(n==1) *b=cipolla::calc(*a);
    else {
        sqrt((n+1)/2,a,b);
        static int c[N];
        inve(n,b,c);
        mult(n,a,c,c);
        for(int i=0;i<n;i++) b[i]=(b[i]+c[i])*inv[2]%mod;
    }
}
void deri(int n,int *a,int *b) {
    for(int i=0;i<n-1;i++) b[i]=a[i+1]*(i+1)%mod;
    b[n-1]=0;
}
void inte(int n,int *a,int *b) {
    for(int i=n-1;i>0;--i) b[i]=a[i-1]*inv[i]%mod;
    b[0]=0;
}
void loge(int n,int *a,int *b) {
    static int c[N];
    inve(n,a,b);
    deri(n,a,c);
    mult(n,b,c,b);
    inte(n,b,b);
}
void expr(int n,int *a,int *b) {
    if(n==1) *b=1;
    else {
        expr((n+1)/2,a,b);
        static int c[N];
        loge(n,b,c);
        for(int i=0;i<n;i++) c[i]=(a[i]-c[i]+mod)%mod;
        c[0]=(c[0]+1)%mod;
        mult(n,b,c,b);
    }
}
}

int n,m,a[N],b[N],c[N],cnt[N];

signed main() {
    ios::sync_with_stdio(false);
    cin>>n>>m;
    po::presolve((m+1)<<1);
    for(int i=1;i<=n;i++) {
        int tmp;
        cin>>tmp;
        cnt[tmp]++;
    }
    for(int k=1;k<=m;k++) {
        vector<int> fac;
        int i;
        for(i=1;i*i<k;i++) if(k%i==0) fac.push_back(i),fac.push_back(k/i);
        if(i*i==k) fac.push_back(i);

        for(int j:fac) {
            a[k]+=cnt[k/j]*inv(j)%mod;
            a[k]%=mod;
        }
    }
    po::expr(m+1,a,b);
    for(int i=1;i<=m;i++) cout<<b[i]<<endl;
}