工业机器人工具坐标系(TCF)标定的六点法原理
Posted beta-1999
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了工业机器人工具坐标系(TCF)标定的六点法原理相关的知识,希望对你有一定的参考价值。
一、基本步骤
(1)在机器人动作范围内找一个非常精确的固定点作为参考点;
(2)在工具上确定一个参考点(最好是工具中心点Tool Center Point, TCP);
(3)手动操纵机器人的方法移动TCP,以四种不同的工具姿态与固定点刚好碰上。
??前三个点任意姿态,第四点是用工具的参考点垂直于固定点,第五点是工具参考点从固定点向将要设定的TCP的x方向移动,第六点是工具参考点从固定点向将要设定的TCP的在z方向移动,如下图所示:
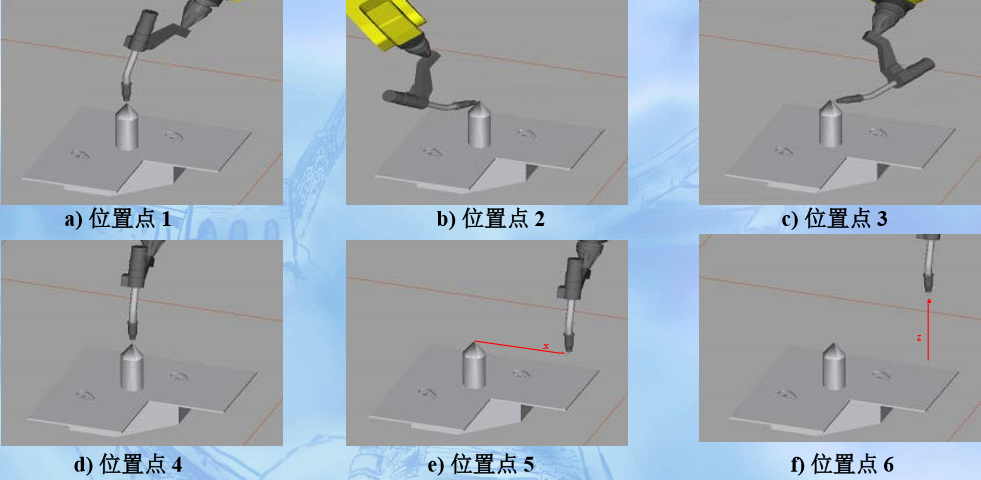
(4)通过前4个点的位置数据即可计算出TCP的位置,通过后2个点即可确定TCP的姿态
二、标定过程
1、TCP位置标定
??假设取1、2、3、4四个标定点之间相差90°且不在同一平面上,如下图所示:
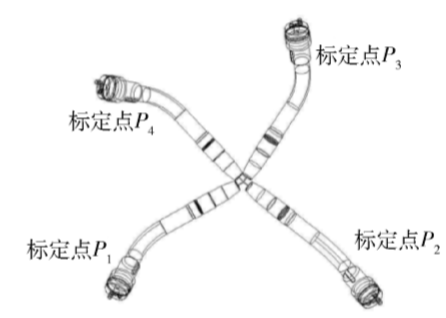
??给定如下坐标系定义:
【1】基坐标系(0坐标系):B
【2】末端坐标系:E
【3】工具坐标系:T
??给定如下变换矩阵定义:
【1】末端坐标系 E 相对于基坐标系 B的变换关系 :(^{B}_ {E}T)
【2】工具坐标系T 相对于末端坐标系 E的变换关系 :(^{E}_ {T}T)
【3】工具坐标系T 相对于基坐标系 B的变换关系 :(^{B}_ {T}T)
??显然可以知道:
$$^{B}_ {E}T · ^{E}_ {T}T = ^{B}_ {T}T ag{1}$$
??对于选定位置点 i = 1、2、3、4,有:
??【1】(^{B}_ {E}T)不等,设:
??【2】(^{E}_ {T}T)不等,但其位置(^{E}P_ {T})相等,设:
??【3】(^{B}_ {T}T) 不等,但其位置(^{E}P_ {T})相等,设:
??关注公式(2)、(3)、(4)中加粗符号,有:
??在实际中,(^{B}_ {E}T) 由机器人正解方程可以直接测得,因此,我们直接读取四个位置点的姿态(^{B}_ {E}R_ {i})和位置(^{B}P_ {Ei = 1, 2, 3, 4})。假设:
??则,(6) - (7)得:
??同理可得:
??由(8)、(9)、(10)可得:
??由于(^{E}P_ {T})为 3x1 列向量,而等式右边为 9x3的矩阵,因此方程(11)为不相容方程组,不可直接用非齐次线性方程组求解的方法或者solve求解。采用最小二乘法的矩阵形式,因其系数矩阵不是方阵,不可直接求逆, 因此使用广义逆。采用高斯消元法得到:
??则式(12)所求得的(^{E}P_ {T})即为TCP的位置向量。
2、TCF姿态标定
??在第1部分已经得到工具坐标系(TCF)的位置,而计算TCP姿态采用z/x方向标定。
??此过程中TCF的姿态保持不变(如第一节 -- 基本步骤中图所示)。取第一个姿态标定点为位置点4(下图记作标定点1);机器人从位置点4出发,沿+x方向移动一定距离得到位置点5(下图记作标定点2);机器人从位置点4出发,沿+z方向移动一定距离得到位置点6(下图记作标定点3)。如下图所示:
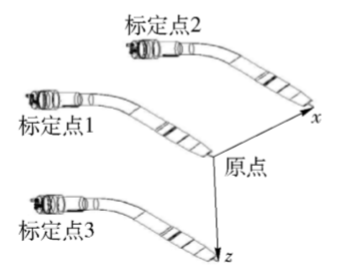
??由于3个标定点中的TCF姿态不变,故(^{B}_ {E}R_{i = 4,5,6})均相等,且由(12)得 (^{E}P_ {T}) 保持不变,故可得到工具坐标系 T 的 x 轴轴向向量 (X) ,且:
??同理,可得到工具坐标系 T 的 z 轴轴向向量 (Z) ,且:
??进而由右手定则得工具坐标系 T 的 y 轴轴向向量 (Y) :
??为进一步保证坐标系矢量的正交性,重新计算(Z) :
??将(13)、(15)、(16)单位化得到(X^{‘}, Y^{‘}, Z^{‘}),得到工具坐标 T 相对于基坐标 B 的姿态(^{B}_ {T}R),且
??又末端坐标系 E 旋转矩阵为(^{B}_ {E}R),且:
??故由(17)、(18)即可得到工具坐标系的旋转矩阵(^{E}_ {T}R),即:
3、TCF标定结果
??由(12)和(19),可得到工具坐标系 (^{E}_ {T}T) 标定为:
??显然,TCF六点法标定的最小条件是能够获取到6个位置点的位姿(^{B}_ {E}T_{i=1,2,3,4,5,6}),且为使式(12)能求解,应保证位置点1,2,3,4不在同一平面上。
三、参考文献
【1】康存锋,王红伟,张鹏飞等.焊接机器人工具坐标系标定的研究与实现[j].北京工业大学学报 2016, 42(1).
【2】兰虎等.《工业机器人技术及应用》.
以上是关于工业机器人工具坐标系(TCF)标定的六点法原理的主要内容,如果未能解决你的问题,请参考以下文章