种群计数------代码之美

Posted 2020-12-05 l2017

种群计数用于统计单位计算机字长所包含的1位的数量。

x是无符号整数，因此右移最高位填0

种群计数

基本方法1：

	int x = 4;//大概208条指令

	int pop = 0;
	for (int i = 0; i<32; i++) {
		if (x & 1)pop = pop + 1;
		x = x >> 1;
	}

基本方法2：

	int x = 6;//大概120~160条指令

	int pop = 0;
	while(x){
		pop = pop + (x & 1);
		x = x >> 1;
	}

基本方法3：

	int x = 6;

	int pop = 0;
	while(x){//循环体需要4或者5条指令，但循环次数等于x中包含的一位数的数目
		pop = pop + 1;
		x = x &(x-1);//x&(x-1)的作用是将x的最低1位清零
	}

查表法：

	int x = 6;//大概17条指令
	static char table[256] = { 0,1,1,2,1,2,2,3,...8 };
	int pop = table[x & 0xFF] + table[(x >> 8) & 0xff] + table[(x >> 16) & 0xFF] + table[x >> 24];

分治法：

 

 	int x = 7;
	x = (x & 0x55555555) + ((x >> 1) & 0x55555555);
	x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
	x = (x & 0x0f0f0f0f) + ((x >> 4) & 0x0f0f0f0f);
	x = (x & 0x00ff00ff) + ((x >> 8) & 0x00ff00ff);
	x = (x & 0x0000ffff) + ((x >> 16) & 0x0000ffff);

　

int pop(unsigned x) {//21条指令
	x = x-((x >> 1) & 0x55555555);
	x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
	x = (x + (x >> 4)) & 0x0f0f0f0f;
	x = x + (x >> 8);
	x = x + (x >> 16);
	return x & 0x0000003f;
}

另外一种方法：

int pop(unsigned x) {//最大适用于62位字长，无法只通过简单地扩展常数适用于64位字长
　　　　　　　　　　　　 //15条指令，但有一条无符号模指令，速度较慢
	unsigned n;
	n = (x >> 1) & 033333333333;//对每个三位字段进行1位计数
	x = x - n;
	n = (n >> 1) & 033333333333;
	x = x - n;
	x = (x + (x >> 3)) & 030707070707;//6位字段的1位数目和
	return x % 63;                   //将所以6位字段和相加
}

　　

两个字种群计数的和与差

pop(x)-pop(y)=pop(x)-(32-pop(~y))

　　　　　　=pop(x)+pop(~y)-32

int popDiff(unsigned x, unsigned y) {//使用32条指令，若使用上面的分治法进行两次运算和一次减法则需要43条指令
	x = x - ((x >> 1) & 0x55555555);
	x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
	y = ~y;
	y = y - ((y >> 1) & 0x555555555);
	y= (y & 0x33333333) + ((y >> 2) & 0x33333333);
	x = x + y;
	x = (x & 0x0f0f0f0f) + ((x >> 4) & 0x0f0f0f0f);
	x = x + (x >> 8);
	x = x + (x >> 16);
	return (x & 0x0000007f) - 32;
}

两个字的种群计数比较

程序返回负值表示pop(x)<pop(y),

返回0则表示pop(x)=pop(y),

返回正值表示pop(x)>pop(y)。

int popCmpr(unsigned xp, unsigned yp) {//对每个字中的单个比特位轮流清零，直到某个字的比特位全为0，那么剩下的非零种群计数值的字就是较大者。大概50条指令
	unsigned x, y;
	x = xp&~yp;//清除同是1的比特位
	y = yp&~xp;//是1的比特位
　　　　　while (1) {
		if (x == 0)return y | -int(y);
		if (y == 0)return 1;
		x = x&(x - 1);//每个字
		y = y&(y - 1);//清除一个1位
	}
}

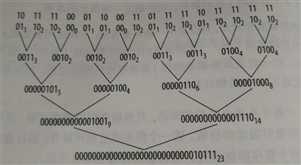
数组中的1位种群计数

//处理2个一组的元素
#define CSA(h,l,a,b,c)//处理进位
	{unsigned u=a^b;unsigned v=c;	h=(a&b)|(u&v);l=u^v;}
int pop(unsigned x) {//21条指令
	x = x - ((x >> 1) & 0x55555555);
	x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
	x = (x + (x >> 4)) & 0x0f0f0f0f;
	x = x + (x >> 8);
	x = x + (x >> 16);
	return x & 0x0000003f;
}
int popArray(unsigned A[], int n) {//平均每字10.5条指令
	int tot, i;
	unsigned ones, twos;
	tot = 0;//初始化
	ones = 0;
	for (i = 0; i <= n - 2; i = i + 2) {
		CSA(twos, ones, ones, A[i], A[i + 1]);
		tot = tot + pop(twos);
	}
	tot = 2 * tot + pop(ones);
	if (n & 1)//如果还剩最后一个字，则把它的种群计数也加上
		tot = tot + pop(A[i]);
	return tot;
}
//CSA操作展开为：
	u = ones^A[i];
	v = A[i + 1];
	twos = (ones&A[i]) | (u&v);
	ones = u^v;

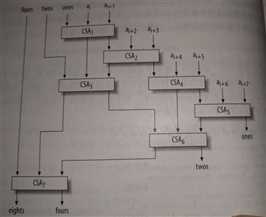
//处理8个一组的元素
#define CSA(h,l,a,b,c)	{unsigned u=a^b;unsigned v=c;	h=(a&b)|(u&v);l=u^v;}
int pop(unsigned x) {//21条指令
	x = x - ((x >> 1) & 0x55555555);
	x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
	x = (x + (x >> 4)) & 0x0f0f0f0f;
	x = x + (x >> 8);
	x = x + (x >> 16);
	return x & 0x0000003f;
}
int popArray(unsigned A[], int n) {//平均每字6.3条指令
	int tot, i;
	unsigned ones, twos, twosA, twosB,
		fours, foursA, foursB, eights;
	tot = 0;//初始化
	fours = twos = ones = 0;
	for (i = 0; i <= n - 8; i = i + 8) {
		CSA(twosA, ones, ones, A[i], A[i + 1]);
		CSA(twosB, ones, ones, A[i + 2], A[i + 3]);
		CSA(foursA, twos, twos, twosA, twosB);
		CSA(twosA, ones, ones, A[i + 4], A[i + 5]);
		CSA(twosB, ones, ones, A[i + 6], A[i + 7]);
		CSA(foursB, twos, twos, twosA, twosB);
		CSA(eights, fours, fours, foursA, foursB);
		tot = tot + pop(eights);
	}
	tot = 8 * tot + 4 * pop(fours) + 2 * pop(twos) + pop(ones);
	for(;i<n;i++)//n不一定能模8整除，所以简单的加上最后的0～7个元素。
		tot = tot + pop(A[i]);
	return tot;
}