第二十四篇 玩转数据结构——队列(Queue)
Posted xuezou
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第二十四篇 玩转数据结构——队列(Queue)相关的知识,希望对你有一定的参考价值。
1.. 队列基础
- 队列也是一种线性结构;
- 相比数组,队列所对应的操作数是队列的子集;
- 队列只允许从一端(队尾)添加元素,从另一端(队首)取出元素;
- 队列的形象化描述如下图:
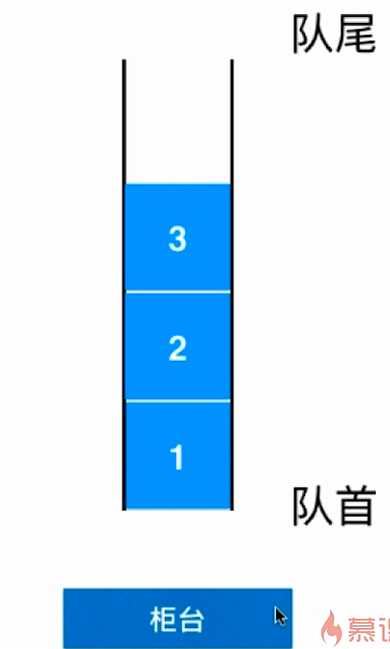
- 队列是一种先进先出(First In First Out)的数据结构;
2.. 队列的实现
- 任务目标如下:
-
Queue<E> ·void enqueue(E) //入队 ·E dequeue() //出队 ·E getFront() //查看队首元素 ·int getSize() //查看队列中元素的个数 ·boolean isEmpty() //查看队列是否为空
- 需要提一下,从用户的角度来看,只要实现上述操作就好,具体底层实现,用户并不关心,实际上,底层确实有多种实现方式。
- 我们准备在之前实现的动态数组基础上,来实现"队列"这种数据结构。
- 先定义一个接口Interface,如下:
-
public interface Queue<E> { int getSize(); boolean isEmpty(); void enqueue(E e); E dequeue(); E getFront(); }
- 实现基于Array类的ArrayQueue类,并进行测试:
-
public class ArrayQueue<E> implements Queue<E> { private Array<E> array; //构造函数 public ArrayQueue(int capacity) { array = new Array<>(capacity); } //无参数构造函数 public ArrayQueue() { array = new Array<>(); } //实现getSize()方法 @Override public int getSize() { return array.getSize(); } //实现isEmpty方法 @Override public boolean isEmpty() { return array.isEmpty(); } //实现getCapacity方法 public int getCapacity() { return array.getCapacity(); } //实现enqueue方法 @Override public void enqueue(E e) { array.addLast(e); } //实现dequeue方法 @Override public E dequeue() { return array.removeFirst(); } //实现getFront方法 @Override public E getFront() { return array.getFirst(); } //方便打印测试 @Override public String toString() { StringBuilder res = new StringBuilder(); res.append("Queue: "); res.append("front ["); for (int i = 0; i < array.getSize(); i++) { res.append(array.get(i)); if (i != array.getSize() - 1) { res.append(", "); } } res.append("] tail"); return res.toString(); } // 测试 public static void main(String[] args){ ArrayQueue<Integer> queue = new ArrayQueue<>(); // 测试入队 for(int i=0;i<5;i++){ queue.enqueue(i); } System.out.println(queue); // 测试出队 queue.dequeue(); System.out.println(queue); } }
- 输出结果:
-
Queue: front [0, 1, 2, 3, 4] tail Queue: front [1, 2, 3, 4] tail
3.. 数组队列的时间复杂度分析:
-
ArrayQueue<E> ·void enqueue(E) O(1) 均摊 ·E dequeue() O(n) ·E getFront() O(1) ·int getSize() O(1) ·boolean isEmpty() O(1)
4.. 循环队列
- 数组队列的出队操作的复杂度是O(n),性能很差,解决方法就是使用循环队列(Loop Queue)
- 循环队列的示意图如下:
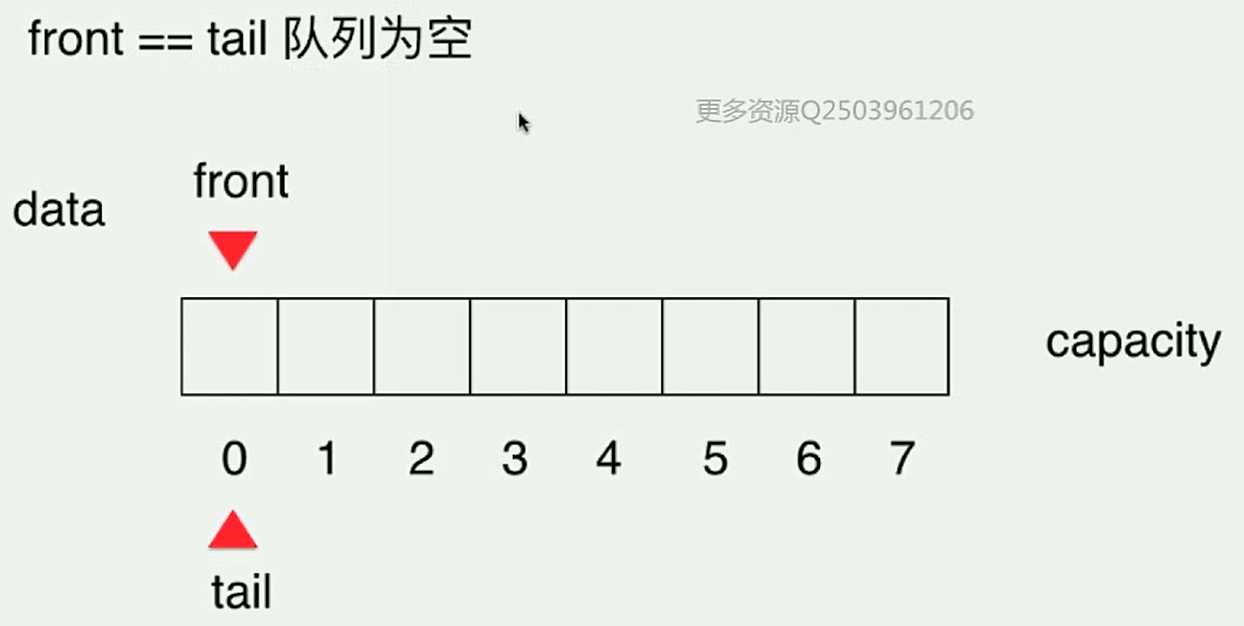
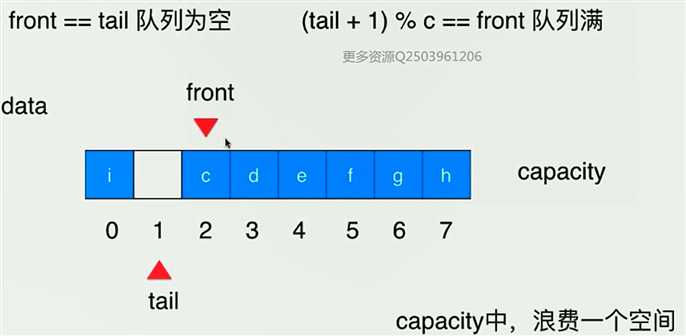
- 实现循环队列的业务逻辑,并进行测试:
-
public class LoopQueue<E> implements Queue<E> { private E[] data; private int front, tail; private int size; //构造函数 public LoopQueue(int capacity) { data = (E[]) new Object[capacity + 1]; front = 0; tail = 0; size = 0; } //无参数构造函数 public LoopQueue() { this(10); //直接调用有参数的构造函数,然后传入一个默认值 } //实现getCapacity方法 public int getCapacity() { return data.length - 1; } //实现isEmpty方法 @Override public boolean isEmpty() { return front == tail; } //实现getSize方法 @Override public int getSize() { return size; } //实现enqueue方法 @Override public void enqueue(E e) { //判断队列是否已满 if ((tail + 1) % data.length == front) { resize(getCapacity() * 2); } data[tail] = e; tail = (tail + 1) % data.length; size++; } //实现dequeue方法 @Override public E dequeue() { //判断队列是否为空 if (isEmpty()) { throw new IllegalArgumentException("Cannot dequeue from an empty queue."); } E ret = data[front]; data[front] = null; front = (front + 1) % data.length; size--; if (size == getCapacity() / 4 && getCapacity() / 2 != 0) { resize(getCapacity() / 2); } return ret; } //实现getFront方法 @Override public E getFront() { if (isEmpty()) { throw new IllegalArgumentException("Queue is empty."); } return data[front]; } //实现resize方法 private void resize(int newCapacity) { E[] newData = (E[]) new Object[newCapacity + 1]; for (int i = 0; i < size; i++) { newData[i] = data[(i + front) % data.length]; } data = newData; front = 0; tail = size; } //方便打印测试 @Override public String toString() { StringBuilder res = new StringBuilder(); res.append(String.format("Queue: size=%d, capacity=%d ", size, getCapacity())); res.append("front ["); for (int i = front; i != tail; i = (i + 1) % data.length) { res.append(data[i]); if ((i + 1) % data.length != tail) { res.append(", "); } } res.append("] tail"); return res.toString(); } //测试 public static void main(String[] args) { LoopQueue<Integer> queue = new LoopQueue<>(); // 测试入队 for (int i = 0; i < 5; i++) { queue.enqueue(i); } System.out.println(queue); // 测试出队 queue.dequeue(); System.out.println(queue); } }
- 输出结果:
-
Queue: size=5, capacity=10 front [0, 1, 2, 3, 4] tail Queue: size=4, capacity=10 front [1, 2, 3, 4] tail
5.. 循环队列的复杂度分析
-
LoopQueue<E> ·void enqueue(E) O(1) 均摊 ·E dequeue() O(1) 均摊 ·E getFront() O(1) ·int getSize() O(1) ·boolean isEmpty() O(1)
6.. 使用简单算例测试ArrayQueue与LoopQueue的性能差异
-
import java.util.Random; public class Main { // 测试使用q运行opCount个enqueue和dequeue操作所需要的时间,单位:秒 private static double testQueue(Queue<Integer> q, int opCount) { long startTime = System.nanoTime(); Random random = new Random(); for (int i = 0; i < opCount; i++) { q.enqueue(random.nextInt(Integer.MAX_VALUE)); } for (int i = 0; i < opCount; i++) { q.dequeue(); } long endTime = System.nanoTime(); return (endTime - startTime) / 1000000000.0; } public static void main(String[] args) { int opCount = 100000; ArrayQueue<Integer> arrayQueue = new ArrayQueue<>(); double time1 = testQueue(arrayQueue, opCount); System.out.println("ArrayQueue, time: " + time1 + " s"); LoopQueue<Integer> loopQueue = new LoopQueue<>(); double time2 = testQueue(loopQueue, opCount); System.out.println("LoopQueue, time: " + time2 + " s"); } }
- 输出结果
-
ArrayQueue, time: 2.88077896 s LoopQueue, time: 0.01140229 s
以上是关于第二十四篇 玩转数据结构——队列(Queue)的主要内容,如果未能解决你的问题,请参考以下文章
C++进阶第二十四篇——布隆过滤器(概念+实现+海量数据处理问题)