基于数据波动性的分割算法

Posted 2020-12-01 showtime20190824

我们常见的分割算法有很多种，比如能量法，包络线法之类的，但这些算法难以实现实时分割，今天我给大家分享一个原创的分割算法，是在以前项目中用过的，这两天加以优化，最中整理了一个MATLAB版本的,给大家分享一下。

算法的原理简单介绍一下：

这里给出了一段肌音信号（已经分割好了），是用加速度传感器在手上采集的，每次完成一次动作，就会产生一个数据波动，如果我们需要分析这样一段信号的特征，需要先将这些信号分割出来。

 

 

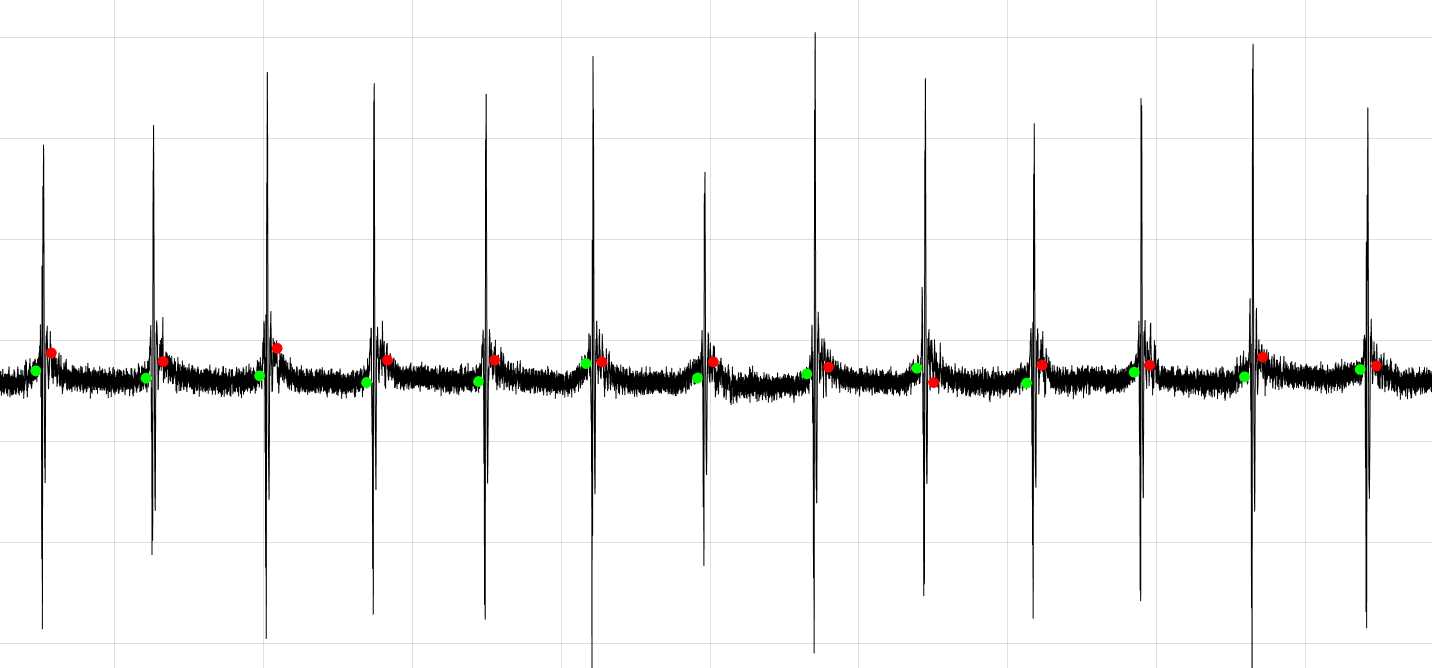
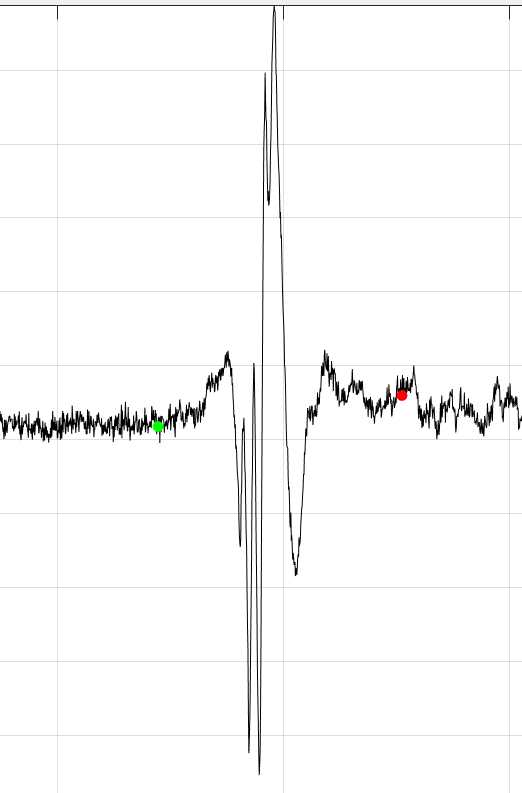
 我们在分析时，主要任务时提取出信号帧起始点对应的数据索引，这里我写了一个分割函数：

function [ST, EN] = SignalDivision(A)

%%宏定义
AF1 = 2;    %放大因子，计算ADD
AF2 = 16;    %放大因子，延申长度
AF3 = 3.5;    %放大因子，判断Frame
MAE = 0.95; %移动平均系数

%%中间变量
L = max(size(A));
AS = MeanAverSlope_3(A);
Sigma = std(A);
ADD = AF1 * (Sigma / AS);
JF = false;
FF = false;
Counter = 1;
Index = 1;
MA = 0;

st = zeros(1, L);
en = zeros(1, L);
ST = zeros(1, L);
EN = zeros(1, L);

DATA_P = zeros(1, L - 1);
DATA_A = zeros(1, L - 2);
DATA_P(1) = A(1);
for i = 2 : L - 1
    DATA_P(i) = DATA_P(i-1) * MAE + A(i) * (1 - MAE); %移动平均
    DATA_A(i-1) = abs(A(i) - DATA_P(i));
    if DATA_A(i-1) > Sigma && ~JF
        JF = true;
        st(Counter) = i - ADD * AF2;
        if ~FF
            ST(Index) = st(Counter);
            FF = true;
        end
    elseif abs(DATA_A(i-1) < Sigma) && JF
        JF = false;
        en(Counter) = i + ADD * AF2;
        sep = en(Counter) - st(Counter);
        Counter = Counter + 1;
    end
    if JF
        if DATA_A(i-1) > MA
            MA = DATA_A(i-1);
        end
    elseif FF
        if i - en(Counter - 1) >sep
            EN(Index) = en(Counter - 1);
            FF = false;
            if MA > Sigma * AF3
                Index = Index + 1;
            end
            MA = 0;
        end
    end
end

ST(ST==0)=[];
EN(EN==0)=[];

function [AS] = MeanAverSlope_3(A)

L = max(size(A));
ALS = zeros(L-1, 1);
for i = 2:L
    ALS(i-1) = abs((A(i) - A(i-1)));
end

AS = mean(ALS);

这个函数主要工作机制是：

1，计算整个波段的数据波动性，用一个“平均斜率”的参数表征，即MeanAverSlope_3 函数的功能，然后再利用公式计算数据的标准差（C/C++的朋友可以自己写一个计算标准差的函数），ADD是断点延伸长度，因为我们判定产生动作的位置比较靠近数据峰值，因此起点需要往前扩展一定距离，终点往后扩展，而ADD即为扩展的长度。

2，利用移动平均的思想消除低频噪音，这些无效的信号往往是由于手的缓慢移动等因素而产生的。我们可以对比消除前后的数据图形：

消除前：

 

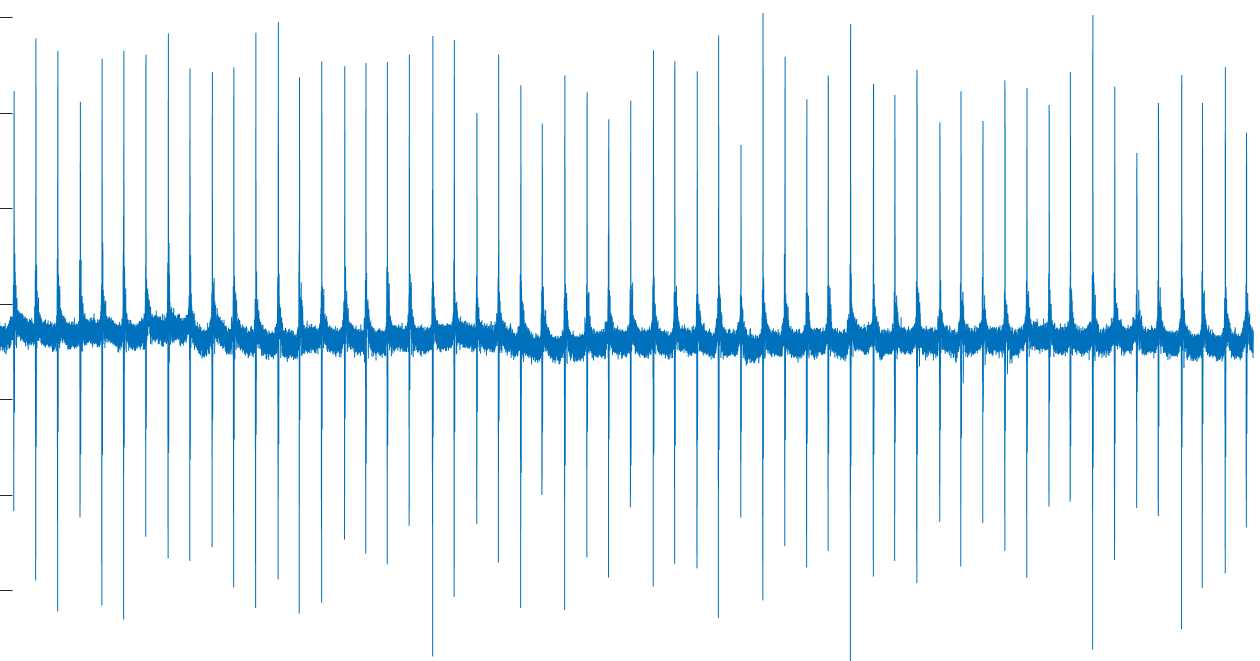
 消除后：

 

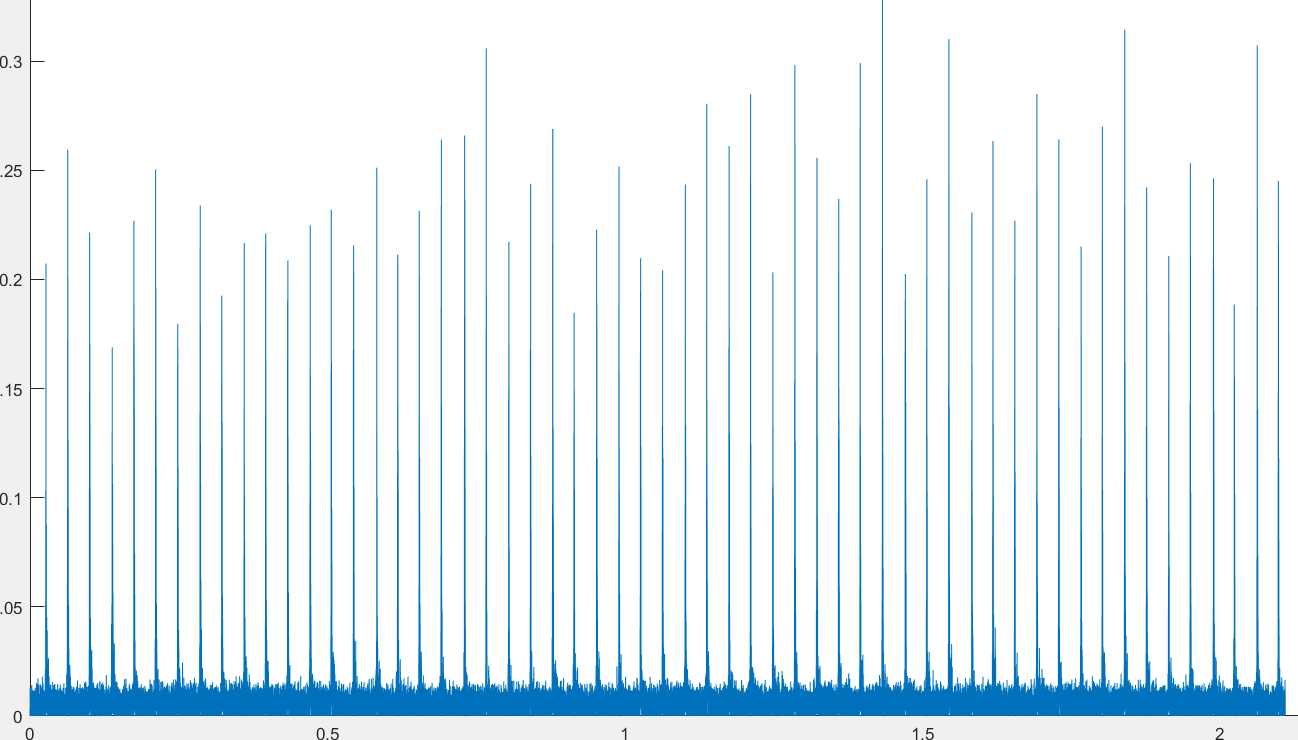
 对比过后，是不是就感觉这样一处理分割起来就简单多了

3，判断数据的跳动性，当数据跳动值大于Sigma时，判定数据有跳动，记录当前对应点的索引值，当一段时间之内还有其他值也大于Sigma时，刷新这个时间，如果没有，则判定该跳动结束，并记录结束位置的索引。然而该跳动是否由手的动作而产生还是环境噪音产生，我们还需要对其进行二次判定，当这段截取的信号中最大跳动值大于阈值 AF3*Sigma 时，才判定该动作有效，否则判定是环境因素产生的噪音。

4，整理数据帧的起始索引，存放于两个向量中，并删除其他数据值为0的点（一开始预分配了内存）

至此，我们的数据分割就完成了，接下来就是怎么用的问题了，由于我们对于数据是一个一个导入处理的（在一个大的for循环中），而不是一段一段或者整段处理，因此该算法具有实时性，非常适合在嵌入式设备中应用。

我们看一下对肌音信号的分割效果：

 

 

 

 

 

 

 

 

 

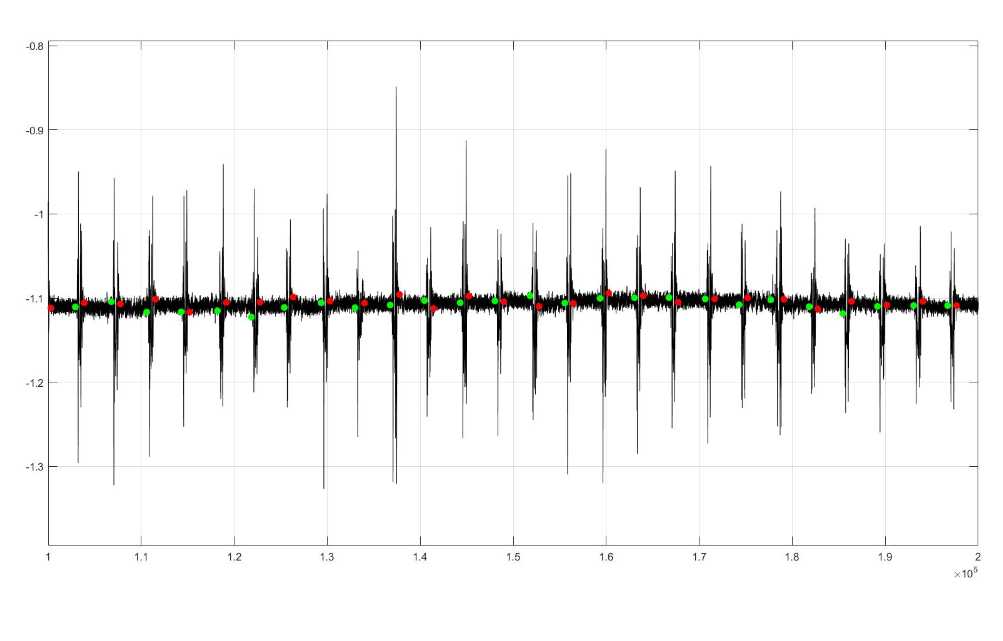
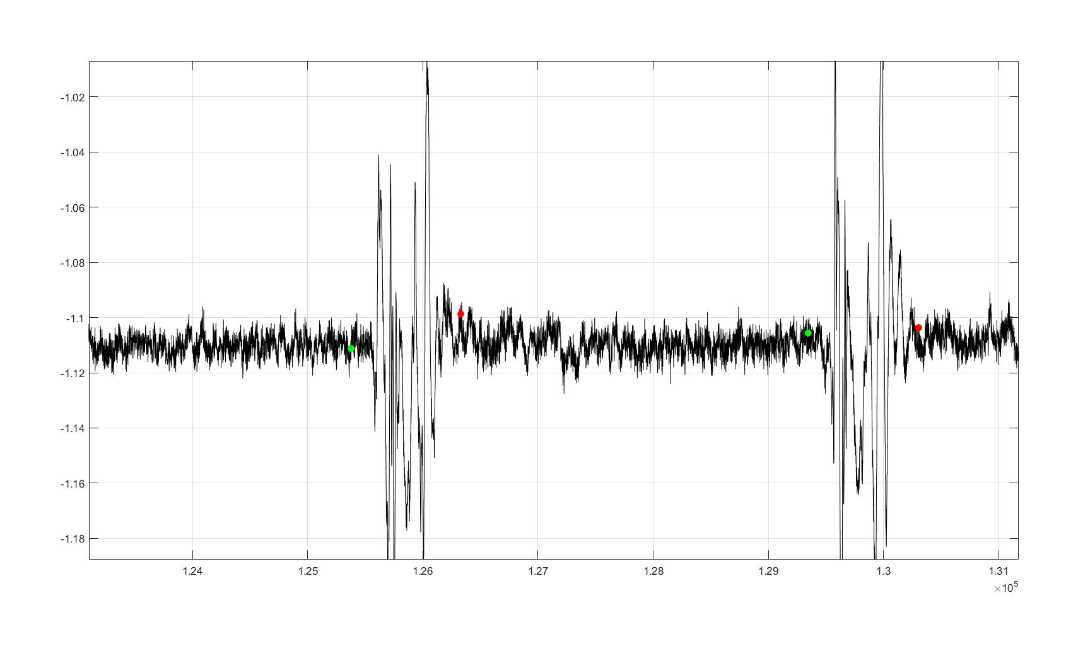
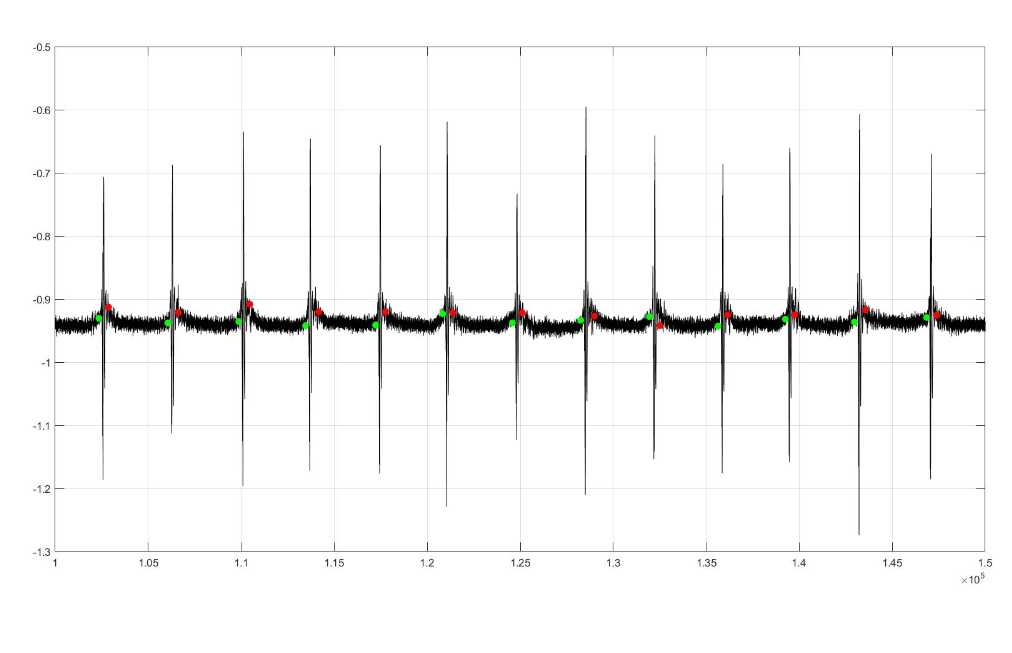
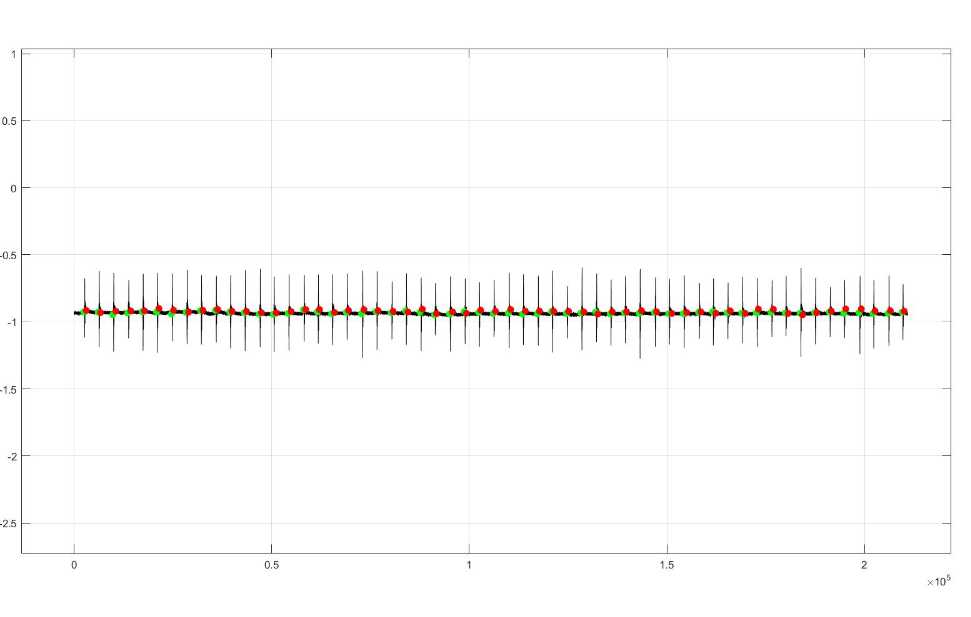
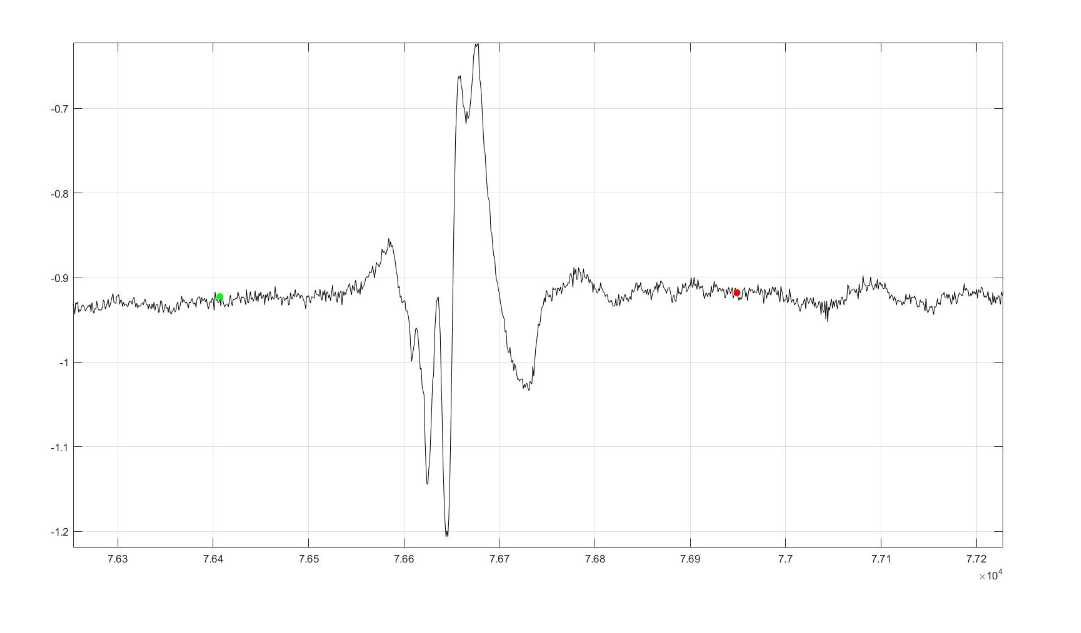
 最后，我要感谢吴荣耀同学，在研究这个算法的时候他帮助了我很多。

觉得有帮助的话记得点赞转发哦！