logistic regression与最大熵模型·逻辑斯蒂回归模型

Posted 2023-02-20 tina_ttl

第6章 logistic regression与最大熵模型（1）·逻辑斯蒂回归模型

标签（空格分隔）： 机器学习教程·李航统计学习方法

---

• 第6章 logistic regression与最大熵模型1逻辑斯蒂回归模型
• Logistic distribution
  • 1 一维逻辑斯蒂分布的数学定义
  • 2 logistic分布的均值和方差
  • 3 何时需要用到Logistic分布
• 二项逻辑斯蒂回归模型及其特点
  • 1 二项逻辑斯蒂回归模型
  • 2 二项逻辑斯蒂回归模型的特点
• 二项逻辑斯蒂回归模型参数的估计
• 多项逻辑斯蒂回归
• 二项逻辑斯蒂回归和多项逻辑斯蒂回归
• 参考文献

逻辑斯蒂：logistic
李航书中称之为：逻辑斯蒂回归模型
周志华书中称之为：对数几率回归模型
Andrew NG书中称之为：逻辑回归
……好吧！好多不同的名称，其实都是一种方法，晕了好久……

---

为了利用逻辑斯蒂分布去进行回归问题的分析，首先，必须知道什么是逻辑斯蒂分布，所以，本节主要讨论逻辑斯蒂分布，它是一个连续分布，与高斯分布非常像；

1 Logistic distribution

The Logistic distribution is a continuous probability density function that is symmetric
and uni-modal. It is similar in appearance to the Normal distribution and in practical
applications, the two distributions cannot be distinguished from one another.

1.1 一维逻辑斯蒂分布的数学定义

• 分布函数
  $$F(x)=\\frac11+e^-(x-\\mu)/\\sigma$$
  注1：也可以写成
  $$F(x)=\\frace^(x-\\mu)/\\sigmae^(x-\\mu)/\\sigma+1$$
  注2：分布函数（即概率累积函数）的导数
  $$F\'(x)=-\\frac(1+e^-(x-\\mu)/\\sigma)\'(1+e^-(x-\\mu)/\\sigma)^2= -\\left ( -\\frac1\\sigma \\right )\\frace^-(x-\\mu)/\\sigma(1+e^-(x-\\mu)/\\sigma)^2= \\frac1\\sigma\\frace^-(x-\\mu)/\\sigma(1+e^-(x-\\mu)/\\sigma)^2$$
• 概率密度函数
  $$f(x)=\\frac1\\sigma* \\frace^-(x-\\mu)/\\sigma(1+e^-(x-\\mu)/\\sigma)^2$$
  
• logistic涉及两个参数
  
  • $\\mu$：location，控制分布函数的中心位置，或者说是概率密度函数对称轴的位置
    
  • $\\sigma$：scale，该参数控制着$f(x)$的宽和高；其值越大，$f(x)$越矮越胖
    
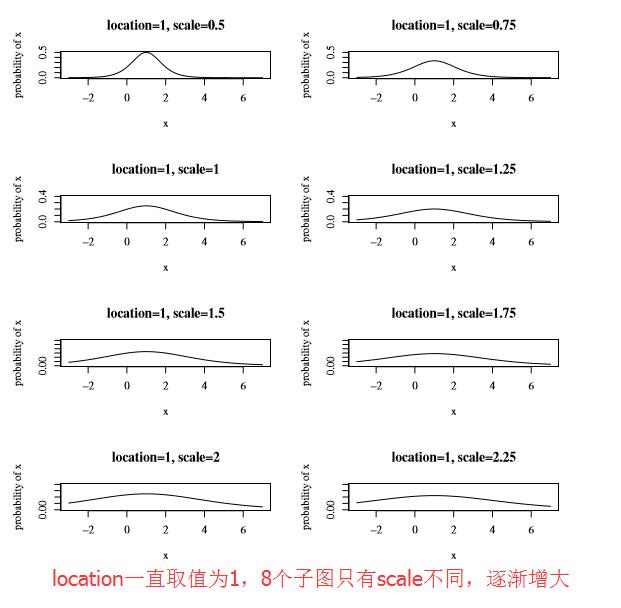
    注：其实该参数$\\sigma$与正态分布的$\\sigma$含义相同，只不过相差了一个系数$\\frac\\pi^23$（这个数字来自于logistic distribution的方差），

1.2 logistic分布的均值和方差

• 均值： $$E(x) = \\mu$$
• 方差： $$Var(x) = \\frac13(\\pi \\sigma)^2$$
• 考察高斯分布$N(\\mu,\\sigma^2)$，它的均值为$\\mu$，方差为$\\sigma^2$：
  
  • 可以看到，logistic分布的方差 σ<

    以上是关于logistic regression与最大熵模型·逻辑斯蒂回归模型的主要内容，如果未能解决你的问题，请参考以下文章

    logistic regression与最大熵模型·逻辑斯蒂回归模型

    logistic regression与最大熵模型·逻辑斯蒂回归模型

    Logistic Regression几问

    Logistic Regression几问

    逻辑斯谛回归与最大熵模型-《统计学习方法》学习笔记

    第六章 逻辑斯蒂回归与最大熵模型