C和Python实现快速排序-三数中值划分选择主元（非随机）

Posted 2023-02-09 LeonYi

一、快排基础

1.1 快排的流程

将数组A进行快速排序的基本步骤-quick_sort(A)：

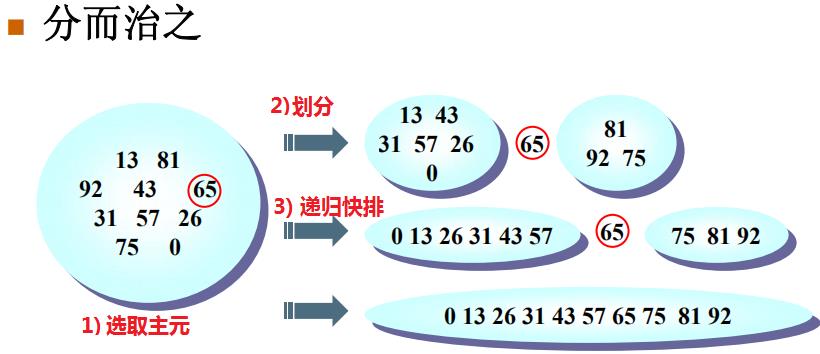
• 递归基础情况：如果A中的元素个数是1或0，则返回。
• 选取主元：取A中的任意一个元素v，作为主元(pivot)。
• 交换策略：将A-v即A中剩余元素，划分成两个不相交的集合（多重集）A1和A2，
• 递归处理：递归调用quick_sort(A1)，再调用quick_sort(A2)

伪代码

可视化快排

选取主元后，将原数组划分为：值小于等于主元的左子数组，值大于等于主元的右子数组。然后递归地对左右子数组进行上述操作，知道递归的基础情况直接返回子数组（递归调用的过程类似二叉树的前序遍历）。

比较基础的情况： 输入数组大小为3， 选取主元并划分后，左子数组和右子数组包含1个数，递归调用快排直接返回，此时已经是有序的。

1.2 主元选取

选取主元： 最优选取到输入数组的中位数，可以均衡进行递归处理。

1）如果直接选择输入数组的第一个元素，在输入数组是有序的情况下，那么将导致快排的最坏情况-平方复杂度。

左边每次取一个最小数，每次划分的复杂度和长度成线性递减，但需划分N-1次

2）随机选取主元： 代价不小

3）三数中值分割法：返回Left, Center, Right三个数中的中位数作为主元，避免最坏情况

• 先让Left<=Center, Left<=Right（若已满足不用管，不满足则交换元素）, 使Left是最小数；
• 那么只需要确定Center, Right的大小。直接通过交换，让Center<=Right, Center即中位数

这时，三数中的最小者被分配在A[Left]，其小于pivot; 最大者被分配在A[Right], 其大于pivot。

可以把pivot放在 A[Right - 1]并在分割阶段，将左右开始索引i=left, j=right-1（A[Right]已经划分好了）

Left和Right为输入数组的左右边界索引。

C语言实现主元选取

typedef int ElementType;
void Swap( int *a, int *b )

     int t = *a;
     *a = *b; 
     *b = t;


ElementType Median3( ElementType A[], int Left, int Right )
   
    int Center = ( Left + Right) / 2;
    if ( A[Left] > A[Center] )
        Swap( &A[Left], &A[Center] );  /* 如果左大于中则交换，保证A[Left] <= A[Center] */
     
    if ( A[Left] > A[Right] )
        Swap( &A[Left], &A[Right] );   /* 如果左大于右则交换，保证A[Left] <= A[Right] */
                
    if ( A[Center] > A[Right] )
        Swap( &A[Center], &A[Right] ); /* 如果中大于右则交换，保证A[Center] <= A[Right] */

    /* A[Left] <= A[Cetner] <= A[Right] */
   
    Swap( &A[Center], &A[Right-1] );  /* 将Pivot藏到右边Right-1作为哨兵*/
    return A[Right-1]; /* 返回实际主元值 */

1.3 交换策略

元素的交换策略：左边找大于等于主元，右边找小于等于主元；

刚刚越界时i>=j， i元素 >= 主元, j元素 <= 主元, 两边已经交换好; i和right-1交换，即把主元和大于等于它的值交换。

快排实现-C

void Q_sort( ElementType A[], int Left, int Right )

    if (Right - Left <= 0) 
        return;
     else 
        int i = Left;
        int j = Right - 1;
        ElementType pivot = Median3( A, Left, Right );

        if (Right - Left == 1) 
            return;

        for ( ; ; )     
            while( A[++i] < pivot );  /* 从左边找个大于等于pivot的数 */
            while( A[--j] > pivot );  /* 从右边找个小于等于pivot的数 */
            if ( i < j )  

                Swap( &A[i], &A[j] ); /* 未越界，则交换 */
            
else 
                break;
        
        Swap( &A[i], &A[Right - 1] ); /* restroe pivot*/
        Q_sort( A, Left, i - 1 ); /* from pivot to divid sort */
        Q_sort( A, i + 1, Right );
            


void Quick_sort( ElementType A[], int N )

    Q_sort( A, 0, N-1 );
 

二、Python版快排

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        def swap(nums, i, j):
            nums[i], nums[j] = nums[j], nums[i]

        def median3(nums, left, right):
            center = (left+right) // 2
            if nums[left] > nums[center]:
                swap(nums, left, center)

            if nums[left] > nums[right]:
                swap(nums, left, right)

            if nums[center] > nums[right]:
                swap(nums, center, right)

            swap(nums, center, right-1)
            return nums[right-1]

        def quick_sort(nums, left, right):
            if right-left > 0:
                pivot = median3(nums, left, right)
                if right-left == 1:
                    return
                i, j = left, right-1
                while True:
                    i += 1
                    while nums[i] < pivot: i += 1
                    j -= 1
                    while nums[j] > pivot: j -= 1

                    if i < j:
                        swap(nums, i, j)
                    else:
                        break
                swap(nums, i, right-1)
                quick_sort(nums, i+1, right)
                quick_sort(nums, left, i-1)

        quick_sort(nums, 0, len(nums)-1)
        return nums

arr_len = 输入数组arr长度 = right -left + 1, 需要处理好基准情况：

• Case1: arr_len 小于等1时，直接返回（不处理了）；
• Case2: arr_len =2时, 这时right - left =1，取到的pivot实际为arr[left]， left = center, = right-1, 不需要也不能进入划分子数组阶段（会越界），而且通过median3已经将长为2的数组排序，故可在调用median3后直接当前递归程序；
• Case3: arr_len == 3，上述快排程序已经可以处理， 并可以进一步通过Case1结束递归；
• Case4: arr_len > 3: 进行快排程序，并通过Case1到3结束递归；

处理基准情况，当输入数组较小时，right - left > 5，直接调用内置排序或插入排序处理，避免进一步递归调用。相当于把更下层的递归调用，直接实现而不用快排实现（快排更慢）。

点击查看代码

def quick_sort(arr, left, right):
    if right - left > 5:
        pivot = mcedian3(arr, left, right)
        i = left
        j = right-1
        while True:
            i += 1
            while arr[i] < pivot:
                i += 1
            j -= 1
            while arr[j] > pivot:
                j -= 1
            if i < j:
                swap(arr, i, j)
            else:
                break    
        
        swap(arr, i, right-1)    
        quick_sort(arr, left, i-1)
        quick_sort(arr, i+1, right)    
    else:
        arr[left:right+1] = sorted(arr[left:right+1])

快排的主元选取和划分操作，可以衍生出减治-快速选择。