Pytorch-geometric: Creating Message Passing Networks 构建消息传递网络教程

Posted 2023-01-19 LeonYi

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Pytorch-geometric: Creating Message Passing Networks 构建消息传递网络教程相关的知识，希望对你有一定的参考价值。

一、背景

将卷积运算推广到不规则域通常表示为邻局聚合(neighborhood aggregation)或消息传递(neighborhood aggregation)模式。

\$\\mathbfx^(k-1)_i \\in \\mathbbR^1 \\times D\$表示节点\$i\$在第\$(k-1)\$层的节点特征， \$\\mathbfe_j,i \\in \\mathbbR^1 \\times F\$表示节点\$j\$到节点的\$i\$边特征（可选的），消息传递图神经网络可以描述为：

\\[\\mathbfx_i^(k) = \\gamma^(k) \\left( \\mathbfx_i^(k-1), \\square_j \\in \\mathcalN(i) \\, \\phi^(k)\\left(\\mathbfx_i^(k-1), \\mathbfx_j^(k-1),\\mathbfe_j,i\\right) \\right), \\]

其中, \$\\square\$表示可微且置换不变的聚合函数(aggregation function)，例如, sum、mean或max，消息函数(message function) \$\\phi\$ 和更新函数(update function)\$\\gamma\$均为可微函数，例如MLP。

值得注意的是，一般GNN论文中通常给出的是聚合邻居信息的Aggregator和更新节点表示Updator，其Aggregator对应pytorch-geometric(PyG)中的消息函数和聚合函数。GNN本质上还是在做特征传播。

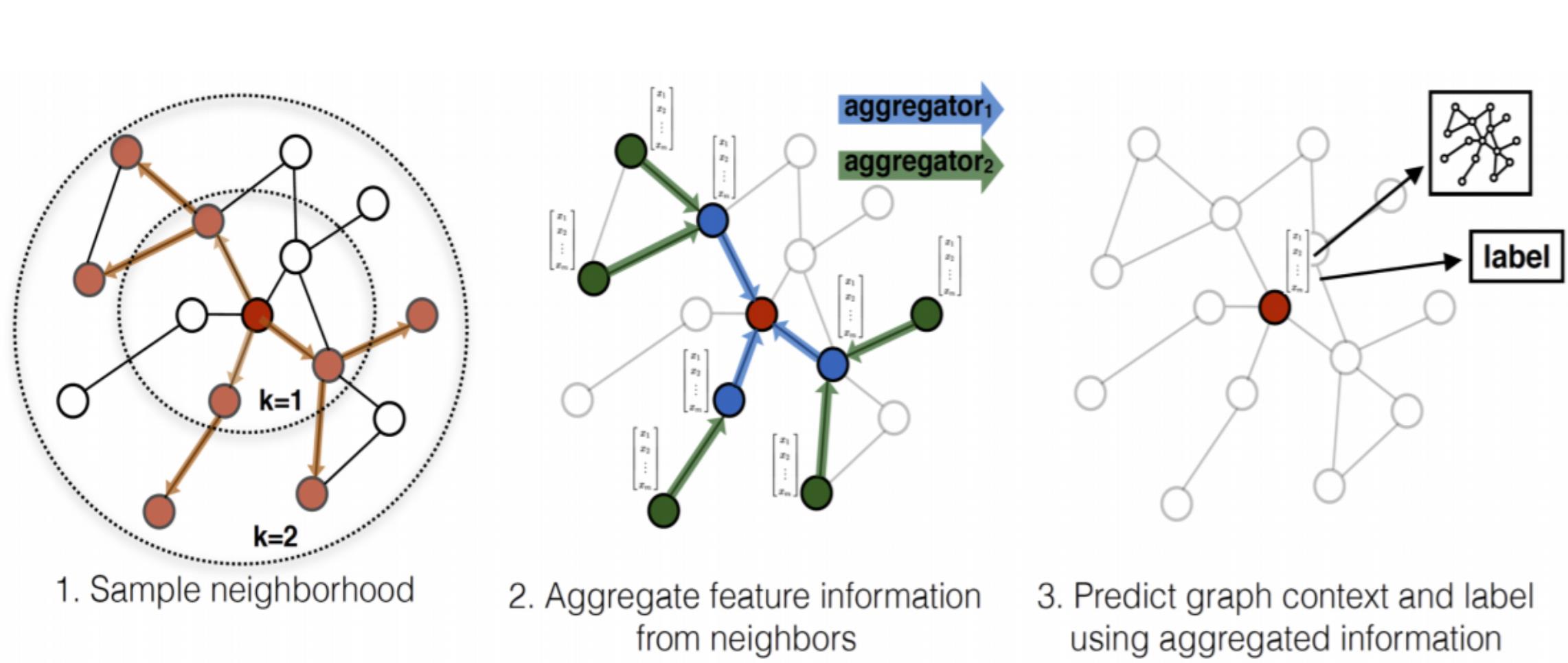
\\[\\mathbfx_\\mathcalN_i^(k)=\\text AGGREGATE _(k)\\left(\\left\\\\mathbfx_j^(k-1), \\forall j \\in \\mathcalN_i\\right\\\\right) \\]

\\[\\mathbfx_i^(k)=\\sigma\\left(\\mathbfW^(k) \\cdot\\left[\\mathbfx_i^(k-1) \\| \\mathbfx_\\mathcalN_i^(k)\\right]\\right) \\]

例如，在GraphSage中，消息函数直接获取邻居节点\$j \\in \\mathcalN_i\$在第\$k-1\$层的嵌入，然后使用mean、max或LSTM作为聚合函数，更新函数将邻居中间嵌入和目标节点\$i\$自身嵌入拼接后做线性变化。

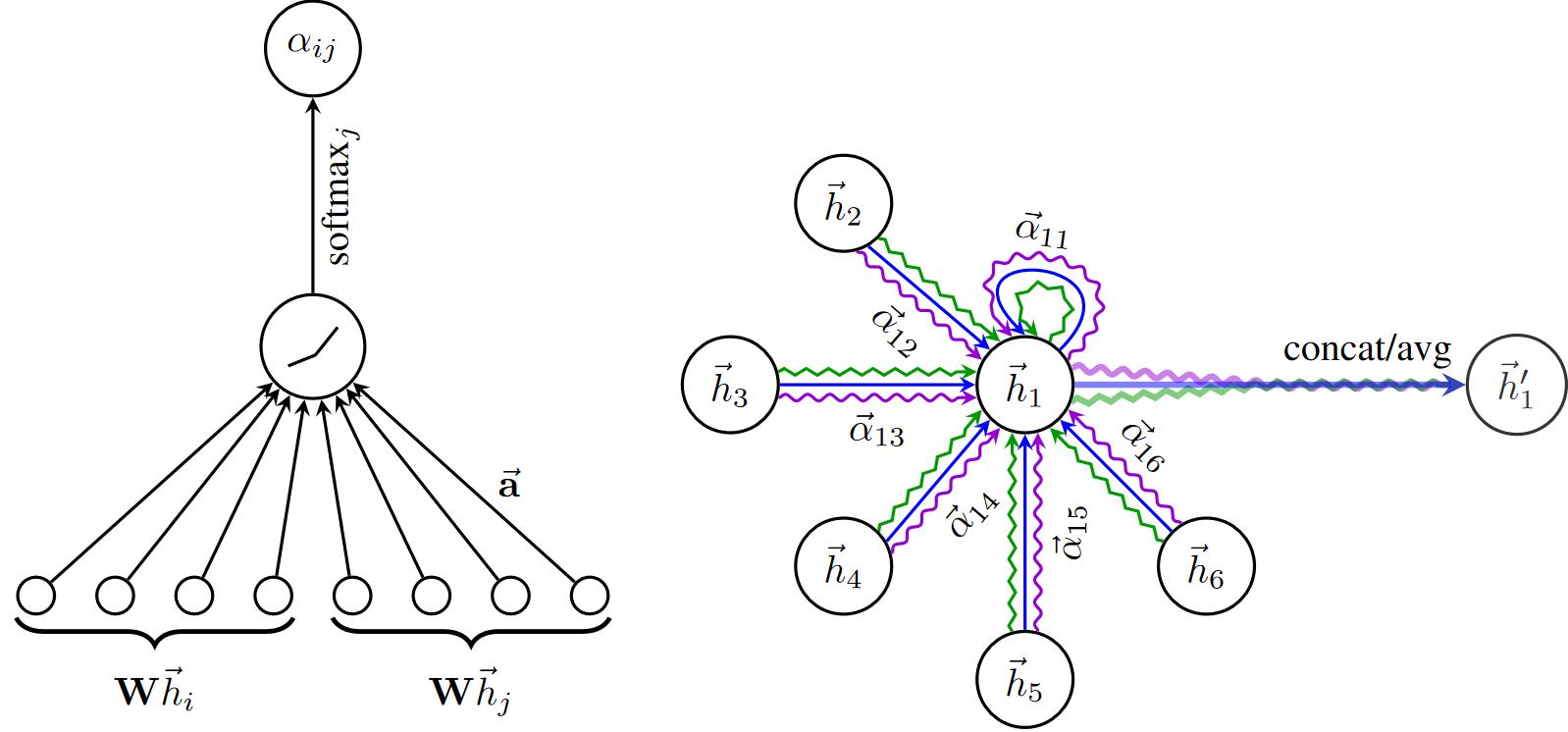
\\[\\alpha_i j=\\frac\\exp \\left(\\text Leaky ReLU \\left(\\mathbfa^T\\left[\\mathbfW \\mathbfx_i \\| \\mathbfW \\mathbfx_j\\right]\\right)\\right)\\sum_k \\in \\mathcalN_i \\exp \\left(\\text Leaky ReLU \\left(\\mathbfa^T\\left[\\mathbfW \\mathbfx_i \\| \\mathbfW \\mathbfx_k\\right]\\right)\\right) \\]

\\[\\mathbfx_i^\\prime=\\|_k=1^K \\sigma\\left(\\sum_j \\in \\mathcalN_i \\alpha_i j^k \\mathbfW^k \\mathbfx_j\\right) \\]

又例如，在GAT中，消息函数根据注意力系数对节点嵌入进行归一化，然后使用"add"作为聚合函数。

二、MessagePassing基类

PyG的torch_geometric.nn中提供了MessagePassing基类，它通过自动处理消息传播来帮助创建此类消息传递图神经网络。用户只需重新定义\$\\phi\$message()和\$\\gamma\$update()及aggregation聚合方式（函数），例如aggr="add", aggr="mean" or aggr="max"，就可以实现自己GNN模型。

借助以下4个方法可实现上述目的：
MessagePassing(aggr="add", flow="source_to_target", node_dim=-2)：定义要使用的聚合方案（"add"，"mean"或"max"）和消息传递的流向（"source_to_target"或"target_to_source"）。此外，node_dim属性指明沿哪个轴传播。

MessagePassing.propagate(edge_index, size=None, **kwargs): 开始传播消息的初始调用。它接收边索引edge_index和构造消息所需的所有其他数据，来更新节点嵌入。propagate()不仅可以在[N, N]的方矩中交换消息，还可通过传入size=(N, M)作为附加参数传递来交换形如[N, M]的稀疏分配矩阵（例如，推荐系统中的二部图）中的消息。如果size设为None，则矩阵为方阵。

MessagePassing.message(...)：类似\$\\phi\$，构造每条边到节点\$i\$的消息。若 flow="source_to_target"则\$(j,i) \\in \\mathcalE\$和flow="target_to_source"则 \$(i,j) \\in \\mathcalE\$。它可接受最初传递给propagate()的任何参数。此外，传递给propagate()的tensors可通过添加后缀_i和_j到变量名（例如，x_i和x_j）映射到对应的节点\$i\$和\$j\$。根据习惯，通常用\$i\$表示聚合信息的中心节点（目标target），并用\$j\$表示邻居节点（源source）。

MessagePassing.update(aggr_out, ...)：类似\$\\gamma\$，更新每个节点\$i \\in \\mathcalV\$的嵌入。聚合操作的输出aggr_out作为其第一个参数，以及最初传递给propagate() 的任何参数。

三、例子

接下来，将通过MessagePassing实现GCN和EdgeConv来作进一步介绍。为便于表示，将节点特征表示为行向量。

3.1 实现GCN层

矩阵形式的GCN层：

\\[\\mathbfX^(k) =\\sigma\\left(\\hat\\mathbfA \\mathbfX^(k-1) \\mathbfW^(k) \\right) \\]

其中，\$\\hat\\mathbfA=\\tilde\\mathbfD^-\\frac12 \\tilde\\mathbfA \\tilde\\mathbfD^-\\frac12 \\in \\mathbbR^N \\times N\$为自环归一化邻接矩阵，\$\\tilde\\mathbfA=\\mathbfA+\\mathbfI\$在原始邻接矩阵上加自环连接, \$\\tilde\\mathbfD=\\mathbfD+\\mathbfI\$，\$\\mathbfX^(k-1)\\in \\mathbbR^N \\times D\$，\$\\mathbfW^(k)\\in \\mathbbR^D\\times D\$。

将\$\\hat\\mathbfA\$在节点层面展开:

\$\\tilde\\mathbfA\$先左乘\$\\tilde\\mathbfD^-\\frac12\$做行变化，即对\$\\tilde\\mathbfA\$的每一行\$\\tilde\\mathbfA_i:\$按节点\$i\$的度\$deg(i)^-\\frac12\$进行归一化（假设\$\\tilde\\mathbfA\$为指示矩阵，除自己之外，只有节点\$i\$的一阶邻居\$j \\in \\mathcalN(i)\$的值\$\\tilde\\mathbfA_ij\$为1)。
\$\\tilde\\mathbfD^-\\frac12 \\tilde\\mathbfA\$再右乘\$\\tilde\\mathbfD^-\\frac12\$做列变化，即对每一列\$(\\tilde\\mathbfD^-\\frac12 \\tilde\\mathbfA)_:j\$按节点\$j\$的度\$deg(j)^-\\frac12\$再做归一化。

此时，\$\\hat\\mathbfA_ij=\\tilde\\mathbfA_ij deg(i)^-\\frac12 deg(j)^-\\frac12\$，即将满足\$\\tilde\\mathbfA_ij \\neq 1\$的边 $ e_ij$ 对应的节点对 \$<i，j>\$的度来进行归一化。

\$\\hat\\mathbfA\$的行或列之和并不为一，它不同于可视为概率转移矩阵的简单行归一化\$\\tilde\\mathbfD^-1 \\tilde\\mathbfA\$或列归一化$\\tilde\\mathbfA \\tilde\\mathbfD^-1 $。

\$\\hat\\mathbfA\$ 右乘 \$\\mathbfX^(k-1)\$，相当于用\$\\hat\\mathbfA\$的每一行的系数对节点的行向量矩阵做线性组合。其中，节点\$i\$在第\$k\$层的表示\$\\mathbfx^(k) \\in \\mathbbR^1 \\times D\$是由 \$\\hat\\mathbfA_i: \\in \\mathbbR^1 \\times N\$乘以\$\\mathbfX^(k-1) \\in \\mathbbR^N \\times D\$，等价于直接以加权系数\$\\hat\\mathbfA_i:\$对节点\$i\$的一阶邻居\$\\mathcalN(i)\$以及\$i\$自己的节点表示做线性组合（加权求和）。

由此，可得到空域视角的GCN层的定义：

\\[\\mathbfx_i^(k) = \\sum_j \\in \\mathcalN(i) \\cup \\ i \\ \\frac1\\sqrt\\deg(i) \\cdot \\sqrt\\deg(j) \\cdot \\left( \\mathbfx_j^(k-1) \\mathbfW^(k) \\right) + \\mathbfb, \\]

其中, 邻居节点的特征先经权重矩阵$\\mathbfW^(k) $做变换，再按它们的度做归一化，最后求和。最后，将偏置向量应用于聚合输出。

GCN公式可分为以下步骤：

将自环连接加到邻接矩阵上
线性变换节点特征矩阵
计算归一化系数
归一化节点特征（制作message的过程）
使用"add"方法聚合节点特征（先汇聚邻居节点特征，再和目标节点特征合并）
加上偏置向量（bias为可选项）。

第1-3步通常在消息传递前计算，4-5步可用MessagePassing基类轻松实现。完整实现如下所示：

点击查看代码

import torch
from torch.nn import Linear, Parameter
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        # in_channels为输入节点特征维度, out_channels为输出节点特征维度
        # 初始化GCN层中的线性变换权重矩阵和bias向量
        super().__init__(aggr=\'add\')  # "Add" aggregation (Step 5).
        self.lin = Linear(in_channels, out_channels, bias=False)
        self.bias = Parameter(torch.Tensor(out_channels))
        self.reset_parameters()

    def reset_parameters(self):
        # 参数初始化
        self.lin.reset_parameters()
        self.bias.data.zero_()

    def forward(self, x, edge_index):
        # 节点特征矩阵x的shape为[N, in_channels]
        # 边索引edge_index的shape为[2, E]

        # Step 1: 将自环连接加到邻接矩阵上
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

        # Step 2: 对节点特征矩阵做线性变换
        x = self.lin(x)

        # Step 3: 计算归一化系数
        row, col = edge_index # 分别取出边索引的两部分
        # 由于GCN一般将图视为无向，row或col中分别包含所有节点的索引，故可根据col统计节点的度
        deg = degree(col, x.size(0), dtype=x.dtype) # 度对角矩阵
        deg_inv_sqrt = deg.pow(-0.5) # 对角元素开负根号
        deg_inv_sqrt[deg_inv_sqrt == float(\'inf\')] = 0
        # 归一化系数实际对应每条边，直接用边索引取度相乘即可
        # norm的shape为[E, 1], E为边数量
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]

        # Step 4-5:开始传播消息
        out = self.propagate(edge_index, x=x, norm=norm)

        # Step 6: 加偏置向量
        out += self.bias

        return out

    def message(self, x_j, norm):
        # x_j的shape为[E, out_channels]
        # Step 4: 归一化节点特征(先将norm系数变为列向量，再和x_j做点乘)
        return norm.view(-1, 1) * x_j

GCNConv继承了使用"add"聚合操作的MessagePass。GCN层的所有计算逻辑都包含在其forward方法中。

在计算好归一化系数norm后(在GCN中norm固定)，将调用propagate()，该函数内部会调用message()、update()和aggregate() 。除了edge_index, 节点嵌入x和归一化系数norm将作为GCN消息传播的附加参数。

在message()函数中，需通过norm对邻居节点特征进行归一化。这里，x_j表示一个 a lifted tensor，它包含每个边的source源节点特征，即每个节点的邻居。

以上就是创建一个简单的消息传递层所需的全部内容。此层可用作深层GNN的基础模块。初始化和调用它很简单：

点击查看代码

conv = GCNConv(16, 32)
x = conv(x, edge_index)

3.2 实现EdgeConv层

边卷积层可以处理处理图或点云，它在数学上定义为：

\\[\\mathbfx_i^(k) = \\max_j \\in \\mathcalN(i) h_\\mathbf\\Theta \\left( \\mathbfx_i^(k-1), \\mathbfx_j^(k-1) - \\mathbfx_i^(k-1) \\right), \\]

其中，\$h_\\mathbf\\Theta\$表示MLP。与GCN层类似，可使用MessagePassing类来实现它，聚合方式将使用"max"：

点击查看代码

import torch
from torch.nn import Sequential as Seq, Linear, ReLU
from torch_geometric.nn import MessagePassing

class EdgeConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super().__init__(aggr=\'max\') #  "Max" aggregation.
        self.mlp = Seq(Linear(2 * in_channels, out_channels),
                       ReLU(),
                       Linear(out_channels, out_channels))

    def forward(self, x, edge_index):
        # x has shape [N, in_channels]
        # edge_index has shape [2, E]

        return self.propagate(edge_index, x=x)

    def message(self, x_i, x_j):
        # x_i has shape [E, in_channels]
        # x_j has shape [E, in_channels]

        tmp = torch.cat([x_i, x_j - x_i], dim=1)  # tmp has shape [E, 2 * in_channels]
        return self.mlp(tmp)

在message()函数内部，self.mlp用于变换目标节点的特征x_i和每条边 \$(j,i) \\in \\mathcalE\$的相对源节点特征 x_j - x_i。边卷积实际为是动态卷积，对GNN的每一层都在特征空间使用knn最近邻来重新计算图结构。

参考文献

[1] Pytorch-geometric官方文档-Creating Message Passing Networks
[2] https://blog.csdn.net/morgan777/article/details/121183287
[3] https://zhuanlan.zhihu.com/p/130796040
[4] https://blog.csdn.net/weixin_39925939/article/details/121360884

以上是关于Pytorch-geometric: Creating Message Passing Networks 构建消息传递网络教程的主要内容，如果未能解决你的问题，请参考以下文章

Pytorch-geometric: Creating Message Passing Networks 构建消息传递网络教程

pytorch-geometric 从入门到不放弃 day3