[概率论与数理统计]笔记：3.3 随机向量的函数的分布与数学期望

Posted 2023-01-12 feixianxing

这篇笔记记录了随机向量的函数的分布，在离散型随机向量函数的内容中简单介绍了解题思路，在连续型随机向量内容中推导了卷积公式，最后简单地记录了一些公式。

3.3 随机向量的函数的分布与数学期望

离散型随机向量的函数的分布

定义

• 离散型随机向量\\((X,Y)\\)的分布为

  \\[P\\X=x_i,Y=y_j\\=p_ij,\\quad i,j=1,2,\\cdots, \\]

• 随机向量的函数为\\(Z=g(X,Y)\\)，记其所有可能取值为\\(z_k(k=1,2,\\cdots)\\)

• \\(Z\\)的概率分布为

  \\[P\\Z=z_k\\=P\\g(X,Y)=z_k\\=\\sum\\limits_g(x_i,y_j)=z_kP\\X=x_i,Y=y_j\\ \\]

解题步骤

1. 绘制随机向量\\((X,Y)\\)的概率分布表。
2. 计算出\\(Z\\)的所有可能取值。
3. 将概率分布表中\\(z_k=g(x_i,y_j)\\)的值相同的项合并相加，即得\\(Z\\)的概率分布。

泊松分布的再生性

如果\\(X,Y\\)相互独立且\\(X\\sim P(\\lambda_1),Y\\sim P(\\lambda_2)\\)，则对于\\(Z=X+Y\\)，有\\(Z\\sim P(\\lambda_1+\\lambda_2)\\).

---

连续型随机向量的函数的分布

定义

设\\((X,Y)\\)是二维连续型随机向量，其概率密度函数为\\(f(x,y)\\)，函数\\(Z=g(X,Y)\\)，则分布函数

\\[\\beginalign* F_Z(z) &= P\\Z\\le z\\=P\\g(X,Y)\\le z\\=P\\(X,Y)\\in D_z\\ \\\\ &= \\iint\\limits_D_zf(x,y)\\mathrmdx\\mathrmdy \\endalign* \\]

其中\\(D_z=\\(x,y)|g(x,y)\\le z\\\\).

而密度函数\\(f_Z(z)=F\'_Z(z)\\).

计算分布函数和密度函数的关键在于：

1. 找出区域\\(D_z\\).
2. 计算二重积分\\(\\iint\\limits_D_zf(x,y)\\mathrmdx\\mathrmdy\\)

卷积公式

公式

如果\\(X,Y\\)相互独立且\\(Z=X+Y\\)，则\\(Z\\)的密度函数为

\\[f_Z(z)=\\int_-\\infty^+\\inftyf_X(x)f_Y(z-x)\\mathrmdx=\\int_-\\infty^+\\inftyf_X(z-y)f_Y(y)\\mathrmdy \\]

这里的积分运算称为函数\\(f_X(x)\\)与\\(f_Y(y)\\)的卷积，记作\\(f_X*f_Y(z)\\).

上述公式可以记为：

\\[f_Z(z)=f_X*f_Y(z)=f_Y*f_X(z) \\]

说明

卷积是一种应用很广泛的运算，这里的卷积公式是两个函数卷积生成一个新函数的一种运算。

关于卷积的相关视频：【官方双语】那么……什么是卷积？

公式推导过程

引例题目

设\\((X,Y)\\)的联合密度函数为\\(f(x,y)\\)，\\(X,Y\\)相互独立，求\\(Z=X+Y\\)的密度函数。

推导过程

首先

\\[F_Z(z)=P\\Z\\le z\\=P\\X+Y\\le z\\=\\iint\\limits_X+Y\\le zf(x,y)\\mathrmdx\\mathrmdy \\]

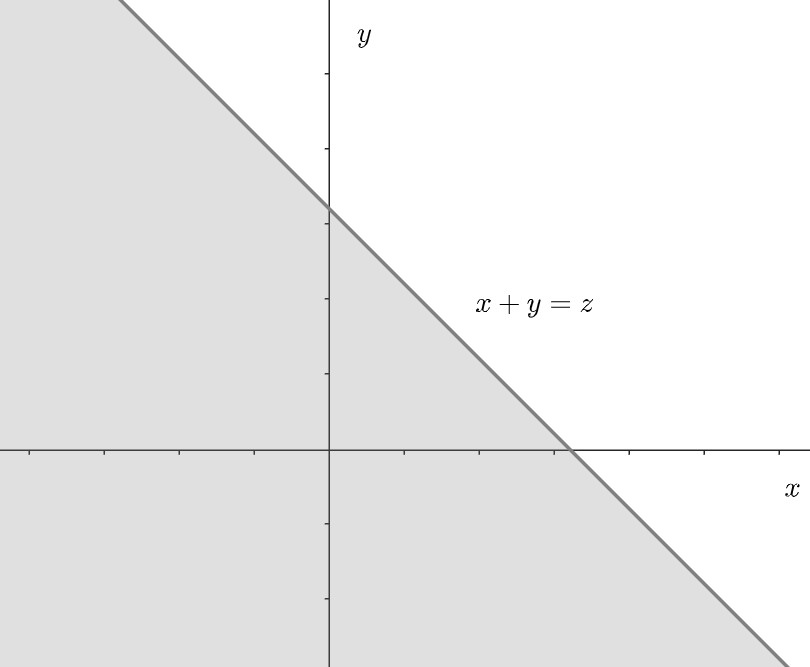
二重积分相关知识点：

• 计算二重积分可以化为两次积分运算。
• 在直角坐标系中，有X型和Y型两种，区别是对于区域的扫描方式。

分界线\\(x+y=z\\)化为\\(y=z-x\\).

对于上述二重积分采用X型，区域的\\(x\\)从\\(-\\infty\\)到\\(+\\infty\\)，\\(y\\)从\\(-\\infty\\)到直线\\(y=z-x\\)，所以

\\[上式=\\int_-\\infty^+\\infty\\mathrmdx\\int_-\\infty^z-xf(x,y)\\mathrmdy \\]

为了使区域更加规范，这里采用换元法，令\\(t=x+y\\)，将\\(y\\)替换为\\(t\\)，上述积分的\\(x\\)部分不变，\\(y\\)部分内：\\(y\\)为变量，\\(x\\)为常量，\\(t=x+y\\)为变量。

积分换元时，需要注意3个部分：

1. 积分上下限的改变
2. 被积函数的改变
3. 积分变量的改变

• 当\\(y\\to-\\infty\\)时，\\(t\\to-\\infty\\)；当\\(y= z-x\\)时，\\(t=x+y=x+(z-x)=z\\).

• 因为\\(y=t-x\\)，所以\\(f(x,y)=f(x,t-x)\\).

• \\(\\mathrmdy=\\mathrmd(t-x)=\\mathrmdt\\).（这里的 \\(x\\) 是常数，可以直接去掉）

因此

\\[上式=\\int_-\\infty^+\\infty\\mathrmdx\\int_-\\infty^zf(x,t-x)\\mathrmdt \\]

注意：此时是二重积分的\\(X\\)型表示。

换元后的区域为\\(t\\le z\\).

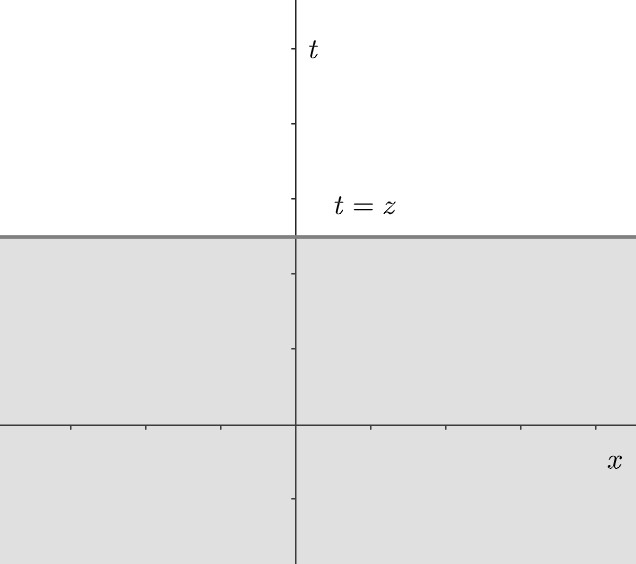
此时，将上述二重积分的\\(X\\)型表示转换为\\(Y\\)型表示。

\\[上式=\\int_-\\infty^+\\infty\\mathrmdx\\int_-\\infty^zf(x,t-x)\\mathrmdt =\\int_-\\infty^z \\left[ \\int_-\\infty^+\\inftyf(x,t-x)\\mathrmdx \\right] \\mathrmdt \\]

一般来说，二重积分\\(X\\)型\\(Y\\)型的互相转换是会导致积分上下限发生改变的，这里因为之前进行了换元，将积分区域转换为了简单的“矩形”，因此积分上下限与原来一样，只是积分次序发生改变。事实上，只要积分区域是“矩形”，就可以随便改变积分次序而不用修改积分上下限。

推导到这里，有：

\\[F_Z(z)=\\int_-\\infty^z \\left[ \\int_-\\infty^+\\inftyf(x,t-x)\\mathrmdx \\right] \\mathrmdt \\]

又因为\\(f_Z(z)=F_Z\'(z)\\)，根据变上限积分求导公式，有：

\\[f_Z(z)=\\int_-\\infty^+\\inftyf(x,z-x)\\mathrmdx \\]

这里的\\(f\\)是\\(X,Y\\)的密度函数，根据上述前提条件：\\(X,Y\\)相互独立，有：

\\[f_Z(z)=\\int_-\\infty^+\\inftyf_X(x)f_Y(z-x)\\mathrmdx \\]

根据对称性，同样的思路可以推导出\\(f_Z(z)=\\int_-\\infty^+\\inftyf_X(z-y)f_Y(y)\\mathrmdy\\).

推导完毕.

正态分布的再生性

若\\(X,Y\\)相互独立且分别服从正态分布\\(N(\\mu_1,\\sigma_1^2)\\)和\\(N(\\mu_2,\\sigma_2^2)\\)，则其任意非零线性组合仍服从正态分布，且

\\[aX+bY\\sim N(a\\mu_1+b\\mu_2,a^2\\sigma_1^2+b^2\\sigma_2^2) \\]

其中\\(a,b\\)不全为0。

这一结论可以推广到\\(n\\)个随机变量的情形。

最大值与最小值

\\(X,Y\\)相互独立，令\\(M=\\max\\X,Y\\\\)，\\(N=\\min\\X,Y\\\\)，则

• \\(M\\)的分布函数为：\\(F_M(z)=F_X(z)F_Y(z)\\).
• \\(M\\)的密度函数为：\\(f_M(z)=f_X(z)F_Y(z)+F_X(z)f_Y(z)\\).
• \\(N\\)的分布函数为：\\(F_N(z)=1-\\left[1-F_X(z)\\right]\\left[1-F_Y(z)\\right]\\).
• \\(N\\)的密度函数为：\\(f_N(z)=f_X(z)\\left[1-F_Y(z)\\right]+f_Y(z)\\left[1-F_X(z)\\right]\\)

---

随机向量的函数的数学期望

设\\(Z=g(X,Y)\\)，

• 对于离散型，有\\(EZ=\\sum\\limits_i\\sum\\limits_jg(x_i,y_j)p_ij\\)

• 对于连续型，有\\(EZ=\\int_-\\infty^+\\infty\\int_-\\infty^+\\inftyg(x,y)f(x,y)\\mathrmdx\\mathrmdy\\)

---

数学期望的进一步性质

1. 如果随机变量\\(X,Y\\)的数学期望都存在，则\\(E(X+Y)\\)存在，且\\(E(X+Y)=EX+EY\\).
2. 如果\\(X,Y\\)相互独立且数学期望均存在，则\\(E(XY)\\)存在，且\\(E(XY)=EX\\cdot EY\\).

使用教材：
《概率论与数理统计》第四版 中国人民大学 龙永红 主编 高等教育出版社