最小生成树MST算法(PrimKruskal)
Posted .SegmentFault
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最小生成树MST算法(PrimKruskal)相关的知识,希望对你有一定的参考价值。
最小生成树MST(Minimum Spanning Tree)
(1)概念
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边,所谓一个 带权图 的最小生成树,就是原图中边的权值最小的生成树 ,所谓最小是指边的权值之和小于或者等于其它生成树的边的权值之和。
(2)性质
-
一个连通图可以有多个生成树;
-
一个连通图的所有生成树都包含相同的顶点个数和边数;
-
生成树当中不存在环;
-
移除生成树中的任意一条边都会导致图的不连通, 生成树的边最少特性;
-
在生成树中添加一条边会构成环。
-
对于包含n个顶点的连通图,生成树包含n个顶点和n-1条边;
-
对于包含n个顶点的无向完全图最多包含
颗生成树。
(3)应用
例如:要在n个城市之间铺设光缆,主要目标是要使这 n 个城市的任意两个之间都可以通信,但铺设光缆的费用很高,且各个城市之间铺设光缆的费用不同,因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树
MST算法之Prim
算法参考地址:Prim的最小生成树(MST)|贪婪的算法-5 - 极客 (geeksforgeeks.org)
Prim算法的流程
1) 创建一组 mstSet,用于跟踪 MST 中已包含的顶点。 2) 为输入图中的所有顶点分配一个键值。将所有键值初始化为 INFINITE。为第一个顶点分配键值为 0,以便首先选取它。 3) 虽然 mstSet 不包括所有顶点 ....a) 选择一个在 mstSet 中不存在且具有最小键值的顶点 u。 ....b) 将 u 包含在 mstSet 中。 ....c) 更新 u 的所有相邻顶点的键值。要更新键值,请循环访问所有相邻的顶点。对于每个相邻的顶点 v,如果边 u-v 的权重小于 v 的前一个键值,则将键值更新为 u-v 的权重使用键值的想法是从剪切中选取最小权重边。键值仅用于尚未包含在 MST 中的折点,这些折点的键值表示将它们连接到 MST 中包含的折点集的最小权重边。
让我们通过以下示例来理解:
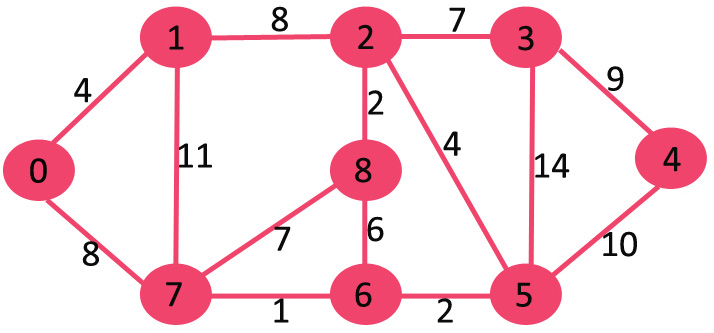
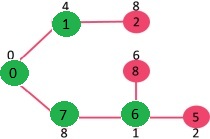
设置的 mstSet 最初是空的,分配给顶点的键是 0, INF, INF, INF, INF, INF, INF, INF,其中 INF 表示无限。现在选取具有最小键值的顶点。选取顶点 0,将其包含在 mstSet 中。因此,mstSet 变得0。包含到 mstSet 后,更新相邻顶点的键值。相邻顶点 0 为 1 和 7。1 和 7 的键值将更新为 4 和 8。下图显示顶点及其键值,仅显示具有有限键值的顶点。MST 中包含的顶点以绿色显示。
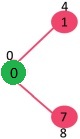
选取具有最小键值且尚未包含在 MST 中(不在 mstSET 中)的顶点。选取顶点 1 并将其添加到 mstSet。所以 mstSet 现在变成 0, 1。更新相邻顶点 1 的键值。顶点 2 的键值变为 8。
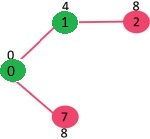
选取具有最小键值且尚未包含在 MST 中(不在 mstSET 中)的顶点。我们可以选择顶点7或顶点2,让顶点7被选中。所以 mstSet 现在变成 0, 1, 7。更新相邻顶点 7 的键值。顶点 6 和 8 的键值变为有限(分别为 1 和 7)。
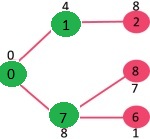
选取具有最小键值且尚未包含在 MST 中(不在 mstSET 中)的顶点。选取顶点 6。所以 mstSet 现在变成 0, 1, 7, 6。更新相邻顶点 6 的键值。顶点 5 和 8 的键值将更新。
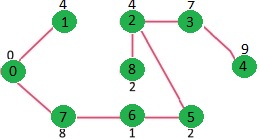
我们重复上述步骤,直到 mstSet 包含给定图形的所有顶点。最后,我们得到下图。
Prim算法的实现(golang)
prim算法的思想和Dijkstra很相似,在理解Dijkstra算法的前提下,理解Prim算法及其实现都会变得非常容易
//graph 中值为math.MaxInt的值为不可达
func prim(graph [][]int, randomVertex int) int
n := len(graph)
//图中已经遍历到的顶点到未遍历的顶点的最短的距离
dist := make([]int, n)
//图中的顶点是否被访问过
visit := make([]bool, n)
//最小生成书的路径和
res := 0
curIdx := randomVertex
//标记初始访问节点
visit[curIdx] = true
//初始化当前节点到未访问节点的距离
for i := 0; i < n; i++
dist[i] = graph[curIdx][i]
//由于已经初始化一个节点,所以只需便利n-1次
for i := 1; i < n; i++
minor := math.MaxInt
for j := 0; j < n; j++
//寻找与已存在节点相接的最短距离的节点
if !visit[j] && dist[j] < minor
minor = dist[j]
curIdx = j
//标记到最短距离的节点为已访问
visit[curIdx] = true
//最短路径值求和
res += minor
//重新初始化已访问节点到未访问节点的距离
for j := 0; j < n; j++
/**
仅更新没有访问过的节点且节点小于当前距离的节点
(因为如果graph[curIdx][j]> dist[j]的话,说明当前已经有节点到节点j的距离更小,
所以此边(graph[curIdx][j])永远也不会被用到)
*/
if !visit[j] && graph[curIdx][j] < dist[j]
dist[j] = graph[curIdx][j]
return res
堆优化版的Prim算法
// Edge 最小生成树prim算法(寻找已知节点到位置节点的最小路径用堆优化)
//graph 中值为math.MaxInt的值为不可达
type Edge struct
startVertex int
endVertex int
weight int
type EdgeHeap []Edge
func (h EdgeHeap) Len() int return len(h)
func (h EdgeHeap) Less(i, j int) bool return h[i].weight < h[j].weight
func (h EdgeHeap) Swap(i, j int) h[i], h[j] = h[j], h[i]
func (h *EdgeHeap) Push(x interface)
*h = append(*h, x.(Edge))
func (h *EdgeHeap) Pop() interface
n := len(*h)
res := (*h)[n-1]
*h = (*h)[:n-1]
return res
func primHeap(graph [][]int, randomVertex int) int
//F代表两点之间不可达
const F = math.MaxInt
n := len(graph)
//图中已经遍历到的顶点到未遍历的顶点的最短的距离
distHeap := make(EdgeHeap, n)
//图中的顶点是否被访问过
visit := make([]bool, n)
//最小生成书的路径和
res := 0
//节点访问数
count := 1
curIdx := randomVertex
//标记初始访问节点
visit[curIdx] = true
//初始化当前节点到未访问节点的距离
for i := 0; i < n; i++
if graph[curIdx][i] != F
distHeap[i] = EdgecurIdx, i, graph[curIdx][i]
heap.Init(&distHeap)
for len(distHeap) > 0 && count < n
edge := heap.Pop(&