关于KMP算法中模式串的移动不会产生漏解的证明

Posted 2021-12-03 onlyblues

　　在KMP算法中我们都知道，当主串与模式串发生失配时，主串的指针不用回溯，而模式串根据最大公共前后缀移动到相应的位置，重新进行匹配，如下图：

　　由于红色的部分是直接被跳过的，因此有个疑问是，这样子移动会不会跳过恰好与模式串匹配的的位置呢？也就是说在红色的这些部分中，是否存在与模式串完全匹配的某个起始位置，如下图：

　　事实上，这种情况是不会成立的。这是因为我们是根据最大公共前后缀来移动模式串，所以保证了这种情况是不会发生的。

　　下面我们用反证法来证这个这个结论是成立的。也就是：如果我们根据最大公共前后缀这一法则来移动模式串，那么在跳过的位置中，不会存在以某一个位置为起点，使得主串与模式串完全匹配。

　　我们先考虑最简单的情况，也就是最大公共前后缀的长度为1的情况：

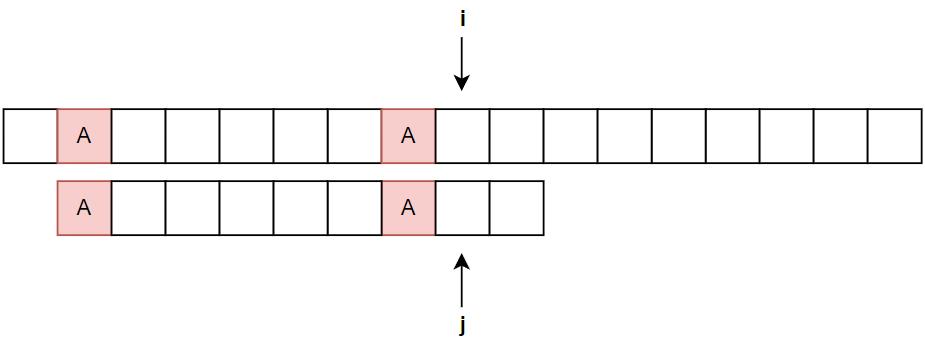
　　然后呢，我们假设存在某一个跳过的位置，以这个位置为起点使得使得主串与模式串完全匹配。

　　然后根据上面的这个匹配结果，我们可以推出下面的结论：

　　也许你现在还发现不了什么，现在让我们把这个模式串再次移动到它之前发生失配的位置：

　　你发现了吗，根据推理的结果，现在模式串中最大公共前后缀是“ABCA”，也就是说最大公共前后缀的长度为4，这与我们一开始的条件“最大公共前后缀长度为1”矛盾了。

　　虽然我们是以最大公共前后缀长度为1进行反证的，但事实上，无论最大公共前后缀的长度为多少，都可以用同样的方法得到相同的结论。比如可以用归纳法。或是对于任意长度的最大公共前后缀，把整个最大公共前后缀等价看作为长度为1，然后用上面的方法同样得证。

　　所以，我们就可以得出一开始的结论了：如果我们根据最大公共前后缀这一法则来移动模式串，那么在跳过的位置中，不会存在以某一个位置为起点，使得主串与模式串完全匹配。

 

参考资料

　　反证法证明：为什么KMP算法不会跳过（漏掉）正确的答案：https://blog.csdn.net/qq_21989927/article/details/109520767