深度学习之梯度下降法

Posted 2021-12-02 ML李嘉图

目录

• 代价函数
• 梯度下降法
• 奇怪的结果

科学家是如何把一个棘手的问题（图像分类）转换成了一个自己熟悉的好量化的问题（优化）。而在深度学习上，我们就是用梯度下降法建立了一个可量化的评判标准——利用“代价”这个标准去判断当前网络模型的参数到底有多好/差，并且给出了往更好的方向前进的一步。

代价函数

在一开始，我们会完全随机地初始化所有的权重和偏置值。可想而知，这个网络对于给定的训练示例，会表现得非常糟糕。例如，输入一个3的图像，理想状态应该是输出层3这个点最亮，

可是实际情况并不是这样。这时就需要定义一个代价函数。

梯度下降法

还得告诉它，怎么改变这些权重和偏置值，才能有进步。

为了简化问题，我们先不去想一个有13000个变量的函数，而考虑简单的一元函数，只有一个输入变量，只输出一个数字。学过微积分的都知道，有时你可以直接算出这个最小值，不过函数很复杂的话就不一定能写出来，而我们这个超复杂13000元的代价函数，就更加是不可能做到的了。

这里我主要关注了两点：

1. 神经网络的代价函数其实是非凸函数
2. 非凸优化问题被认为是非常难求解的，因为可行域集合可能存在无数个局部最优点，通常求解全局最优的算法复杂度是指数级的。

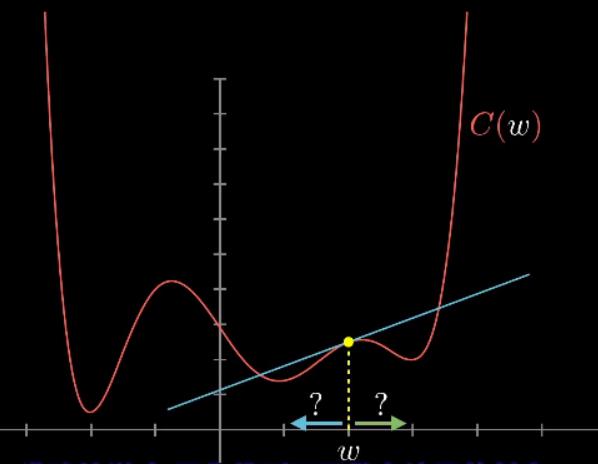
一个更灵活的技巧是：以下图为例，先随便挑一个输入值，找到函数在这里的斜率，斜率为正就向左走，斜率为负则向右走，你就会逼近函数的某个局部最小值。（其实是沿着负梯度方向，函数减小的最快。）

但由于不知道一开始输入值在哪里，最后你可能会落到许多不同的坑里，而且无法保证你落到的局部最小值就是代价函数的全局最小值。

值得一提的是，如果每步的大小和斜率成比例，那么在最小值附近斜率会越来越平缓，每步会越来越小，这样可以防止调过头。

当我们提到让网络学习，实质上就是让代价函数的值最小。代价函数有必要是平滑的，这样我们才能挪动以找到局部最小值，这也就是为什么人工神经元的激活值是连续的。

奇怪的结果

当输入是一个噪声图片时，网络却仍然很自信的把它识别成一个数字。换句话来说，即使网络学会了如何识别数字，但是它却不会自己写数字。

究其原因，因为网络的训练被限制在很小的框架内，在网络的世界里，整个宇宙都是由小网格内清晰的静止的手写数字构成的。

最后，作者给出了上期问题的答案：神经元根本就没有去识别图案和短边！

推荐的资源

1. Chris Olah的博客，特别是讲RNN和LSTM的那篇
2. 视频中提到的 神经网络和深度学习 书的中译本~

引言 | 神经网络与深度学习（不全）

英文链接

Neural networks and deep learning

推荐博客：

深度学习-https://www.cnblogs.com/yeluzi/category/1064181.html

神经网络和深度学习总结-https://blog.csdn.net/myarrow/article/details/51322433