机器学习之逻辑回归以及梯度下降法求解
Posted Icy Hunter
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习之逻辑回归以及梯度下降法求解相关的知识,希望对你有一定的参考价值。
文章目录
前言
逻辑回归,其实不是回归任务,而是分类任务,逻辑回归模型对二分类问题效果较好。
梯度下降法
梯度

import numpy as np
def function_2(x):
return x[0]**2 + x[1]**2
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 生成和x形状相同,所有元素都为0的数组。
print(x.size)
for idx in range(x.size):#0,1
tmp_val = x[idx]
# f(x+h)的计算
x[idx] = tmp_val + h
fxh1 = f(x)#x[0]=x[0]+h,x[1]=x[1]
# f(x-h)的计算
x[idx] = tmp_val - h
fxh2 = f(x)#x[0]=x[0]-h,x[1]=x[1]
grad[idx] = (fxh1 - fxh2) / (2*h)#2*x[0]刚好与h无关,如果f(x)=x[0]**2 + x[1]**2+x[0]就与h相关
x[idx] = tmp_val # 还原值
return grad
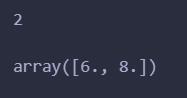
# 求出(3,4)处的梯度
numerical_gradient(function_2, np.array([3.0, 4.0]))
输出:

import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D
#为函数f=function_2(x)在数组x处的梯度,shape=(324,)
def _numerical_gradient_no_batch(f, x):#x.shape=(324,)
h = 1e-4 # 0.0001
grad = np.zeros_like(x)#(324,)
for idx in range(x.size):#从0到323
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
#print(idx)
return grad##(324,)
#f=function_2(x)
def numerical_gradient(f, XX):#参数XX=np.array([X, Y])
if XX.ndim == 1:
return _numerical_gradient_no_batch(f, XX)
else:
grad = np.zeros_like(XX)#(2,324)
for idx, xx in enumerate(XX):#idx=0和1,
#当idx=0时,参数xx=XX[0]=X(324,)
#当idx=1时,参数xx=XX[1]=Y(324,)
#grad[0]为函数F=function_2(x)在数组X处的梯度,shape=(324,)
##grad[1]为函F=数function_2(x)在数组Y处的梯度,shape=(324,)
grad[idx] = _numerical_gradient_no_batch(f, xx)#
#print(idx)
#print(xx)
return grad
def function_2(x):
if x.ndim == 1:
return np.sum(x**2)#对数组每个元素先求平方,再求所有元素的平方的和
else:
##对(2行324列)数组的每个元素先求平方,再求每一行的所有元素的平方的和(沿着行的方向).
#第一行是X的元素,第二行是Y的元素
return np.sum(x**2, axis=1)
if __name__ == '__main__':
x0 = np.arange(-2, 2.5, 0.25)
#print(x0)
#print(x0.shape)#(18,)
x1 = np.arange(-2, 2.5, 0.25)
X, Y = np.meshgrid(x0, x1)
#print(X.shape)#(18, 18)
#print(X)
#print(Y)
X = X.flatten()
Y = Y.flatten()
#print(X.shape)#(324,)
#print(X)
#print(Y)
grad = numerical_gradient(function_2, np.array([X, Y]) )
#print(np.array([X, Y]))
#print(np.array([X, Y]).shape)#(2, 324) 第一行是X的元素,第二行是Y的元素
#print(np.array([X, Y]).ndim)#2
plt.figure()
##参数X,Y:箭头位置的x坐标和y坐标
#-grad[0], -grad[1]:箭头的方向,箭头在x轴,y轴的分量大小
plt.quiver(X, Y, -grad[0], -grad[1], color="#666666")#,headwidth=10,scale=40,color="#444444")
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.xlabel('x0')
plt.ylabel('x1')
plt.grid()
plt.title("fig4-9")
plt.draw()
plt.show()

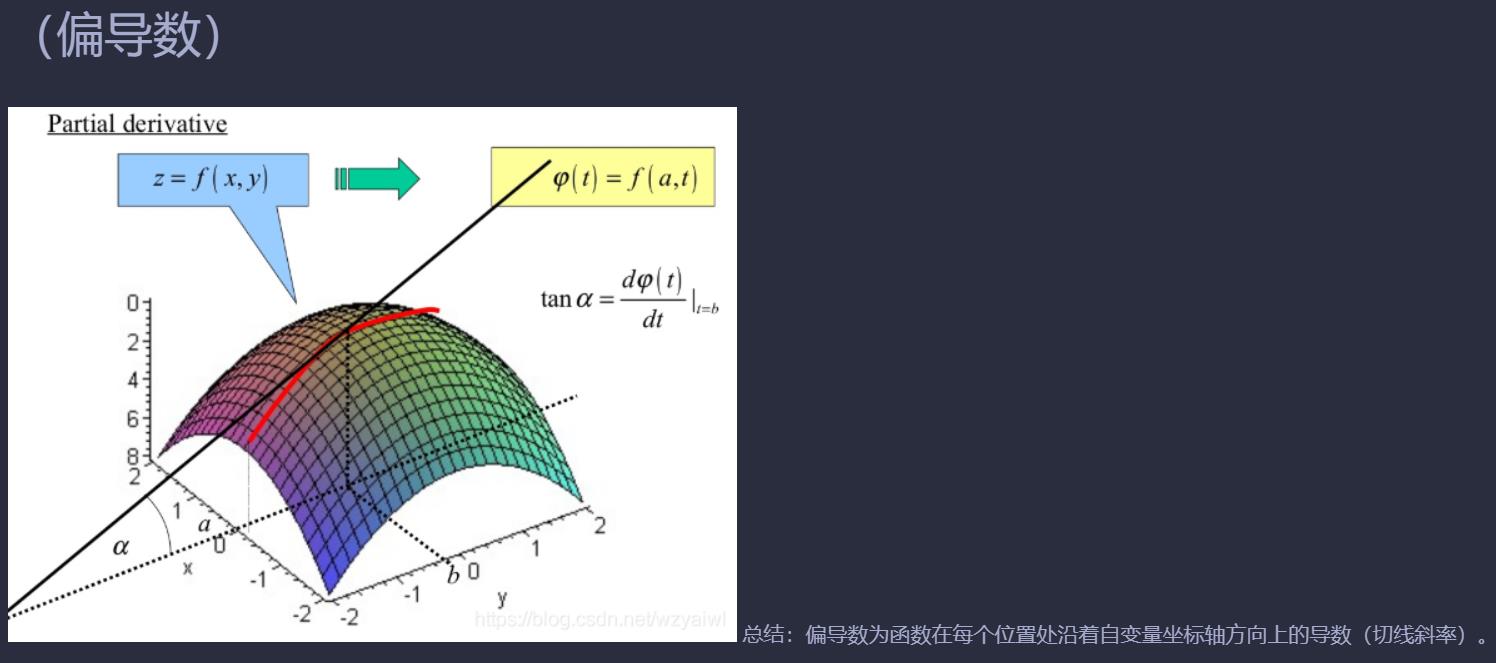

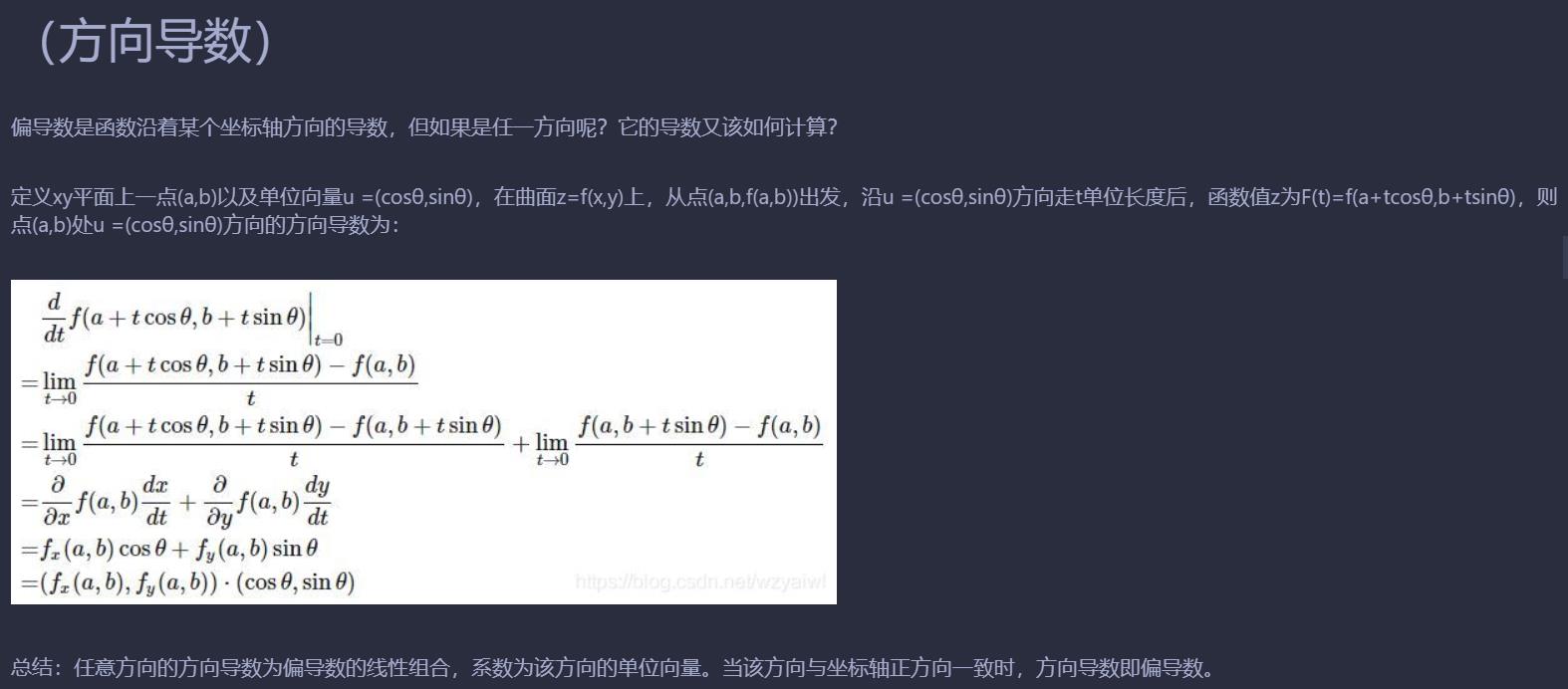


梯度法


def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 生成和x形状相同,所有元素都为0的数组。
for idx in range(x.size):#0,1
tmp_val = x[idx]
# f(x+h)的计算
x[idx] = tmp_val + h
fxh1 = f(x)#x[0]=x[0]+h,x[1]=x[1]
# f(x-h)的计算
x[idx] = tmp_val - h
fxh2 = f(x)#x[0]=x[0]-h,x[1]=x[1]
grad[idx] = (fxh1 - fxh2) / (2*h)#2*x[0]刚好与h无关,如果f(x)=x[0]**2 + x[1]**2+x[0]就与h相关
x[idx] = tmp_val # 还原值
return grad
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
print(grad)
x -= lr * grad
return x
def function_2(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100)
输出:
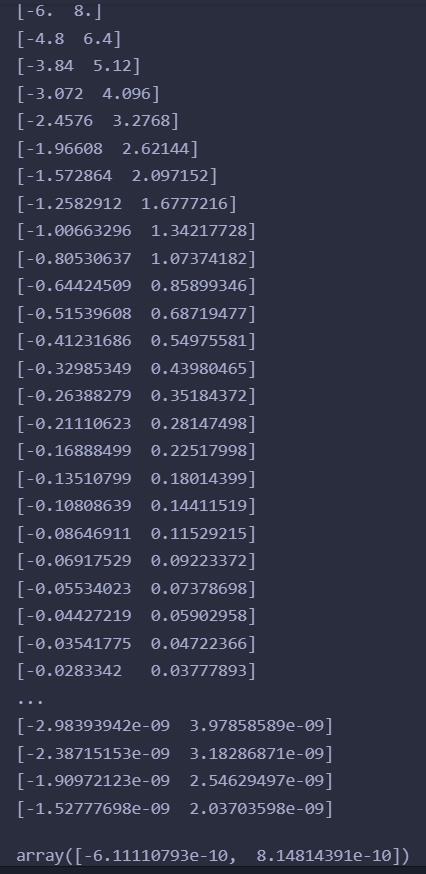
可以看到,函数x1^2 + x2^2的最小值接近(0,0),事实上就是(0,0)梯度下降法得到了近似解。
逻辑回归思路公式推导
我们可以使用线性模型进行回归学习,但若要做的是分类任务,那应该怎么办呢?答案很简单只需要找一个单调可微的函数将
分类任务的真实标记与线性回归模型的预测值联系起来就可以了。

但是,单位阶跃函数并不是连续的。


看得出来,这其实就是一个Sigmoid激活函数,在深度学习中广泛运用。因此,其实可以理解为,二分类就是线性模型的输出进入激活函数,进行非线性变换,得到最终的分类结果(概率)。
因此这个替代函数也可以是别的函数,不过需要满足一些条件,例如任意阶导数都可导,连续等等。

就是将线性模型代入,形成一个复合函数。
里面的未知数就是w向量和b
我们可以变形一下,将线性模型表示在右边(因为分母不可能为0,取倒数再取个对数化一化就化出来了)
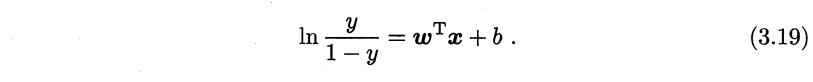

此时我们需要用概率论的知识转换一下表达式。
将y看作正样本的概率,因为是二分类,只有两种情况,那么1-y就是为负样本的概率了。
那么可以用条件概率的知识转换一下表达式。

p(y=1 | x)表示,在x(特征)的情况下,样本为正样本(y=1)的概率
p(y=0 | x)表示,在x(特征)的情况下,样本为负样本(y=0)的概率
此时,又可以变换一下,把左边的ln去掉,即两边同时放在e的指数上:

那么正负样本概率表达式的就能够表示出来了。
如果将正样本的概率表达式记为p1,将负样本的概率表达式即为p0
那么将两个表达式整合成一个表达式:
P(yi|xi) = p01-yip1yi=(1-p1)1-yip1yi
理解起来比较简单,当yi=1(正样本的时候)就为正样本的概率,yi=0(负样本的时候)就为负样本的概率。
那么此时,我们就可以使用极大似然法来估计w向量和b参数了。
极大似然法其实就是求一组参数,使得当前样本出现的概率最大,得出的参数就是极大似然法求出的解。

其中p1就是p(y=1|x)
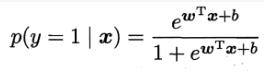
极大似然法就是要求l(w,b)最大值时的w向量和b则是我们需要的模型参数的最终结果。
但是通过观察,我们可以发现,-l(w, b)就类似交叉熵函数
那么现在其实就是求交叉熵损失函数的最小值。
交叉熵损失函数如下:
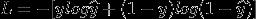
那么可以用梯度下降法进行求解

θ其实就是权重w向量(b并入,特征列加一列1作为偏置项)α就是学习率
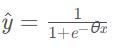
x就是样本特征,y就是样本标签。
具体推导可以看这篇博客:python机器学习手写算法系列——逻辑回归
通过梯度下降法,我们就能够近似求出逻辑回归模型的最优解,从而完成二分类逻辑回归模型的计算。
代码实现
西瓜数据集
data.csv:
色泽_乌黑,色泽_浅白,色泽_青绿,根蒂_硬挺,根蒂_稍蜷,根蒂_蜷缩,敲击_沉闷,敲击_浊响,敲击_清脆,纹理_模糊,纹理_清晰,纹理_稍糊,脐部_凹陷,脐部_平坦,脐部_稍凹,触感_硬滑,触感_软粘,label
0,0,1,0,0,1,0,1,0,0,1,0,1,0,0,1,0,1
1,0,0,0,0,1,1,0,0,0,1,0,1,0,0,1,0,1
1,0,0,0,0,1,0,1,0,0,1,0,1,0,0,1,0,1
0,0,1,0,0,1,1,0,0,0,1,0,1,0,0,1,0,1
0,1,0,0,0,1,0,1,0,0,1,0,1,0,0,1,0,1
0,0,1,0,1,0,0,1,0,0,1,0,0,0,1,0,1,1
1,0,0,0,1,0,0,1,0,0,0,1,0,0,1,0,1,1
1,0,0,0,1,0,0,1,0,0,1,0,0,0,1,1,0,1
1,0,0,0,1,0,1,0,0,0,0,1,0,0,1,1,0,0
0,0,1,1,0,0,0,0,1,0,1,0,0,1,0,0,1,0
0,1,0,1,0,0,0,0,1,1,0,0,0,1,0,1,0,0
0,1,0,0,0,1,0,1,0,1,0,0,0,1,0,0,1,0
0,0,1,0,1,0,0,1,0,0,0,1,1,0,0,1,0,0
0,1,0,0,1,0,1,0,0,0,0,1,1,0,0,1,0,0
1,0,0,0,1,0,0,1,0,0,1,0,0,0,1,0,1,0
0,1,0,0,0,1,0,1,0,1,0,0,0,1,0,1,0,0
0,0,1,0,0,1,1,0,0,0,0,1,0,0,1,1,0,0
划分数据集
def get_data(data):
label = data["label"]
data_ = data.drop(columns=["label"])
return np.array(data_), np.array(label)
data = pd.read_csv("data.csv")
data = shuffle(data)
train_rate = 0.8
num = int(train_rate * len(data))
train_data = data[:num]
test_data = data[num:]
train_x, train_y = get_data(train_data)
test_x, test_y = get_data(test_data)
手写梯度下降法求解二分类逻辑回归模型
import math
##估价函数
def sigmoid(z):
return(1 / (1.0 + math.exp(-z)))
# 逻辑回归模型
def hypothesis(x, theta, feature_number):
'''
x: 一个样本的特征数组
theta:模型参数w向量+bias
feature_number:特征的数量
'''
h = 0.0
# 偏置吸入看作一个特征,方便计算
for i in range(feature_number+1):
h += x[i] * theta[i]
# 模型的输出
return(sigmoid(h))
## 计算偏导数
def compute_gradient(x, y, theta, feature_number, feature_pos, sample_number):
'''
x:样本特征
y:样本标签
theta:模型参数w向量+bias
feature_number:特征的数量
feature_pos:计算第几个特征
sample_number:样本数量
'''
sum = 0.0
for i in range(sample_number):
h = hypothesis(x[i], theta, feature_number)
sum += (h - y[i]) * x[i][feature_pos]
## 平均梯度
return(sum / sample_number)
## 计算损失
def compute_cost(x, y, theta, feature_number, sample_number):
sum = 0.0
for i in range(sample_number):
h = hypothesis(x[i], theta, feature_number)
sum += -y[i] * math.log(h) - (1 - y[i]) * math.log(1 - h)
return(sum / sample_number)
## 梯度下降
def gradient_descent(x, y, theta, feature_number, sample_number, alpha, count):
for i in range(count):
tmp = []
for j in range(feature_number + 1):
tmp.append(0) 机器学习之回归算法