同态加密及其在隐私计算中应用（李增鹏）

Posted 2021-11-22 Pam

视频：链接

同态加密的历史

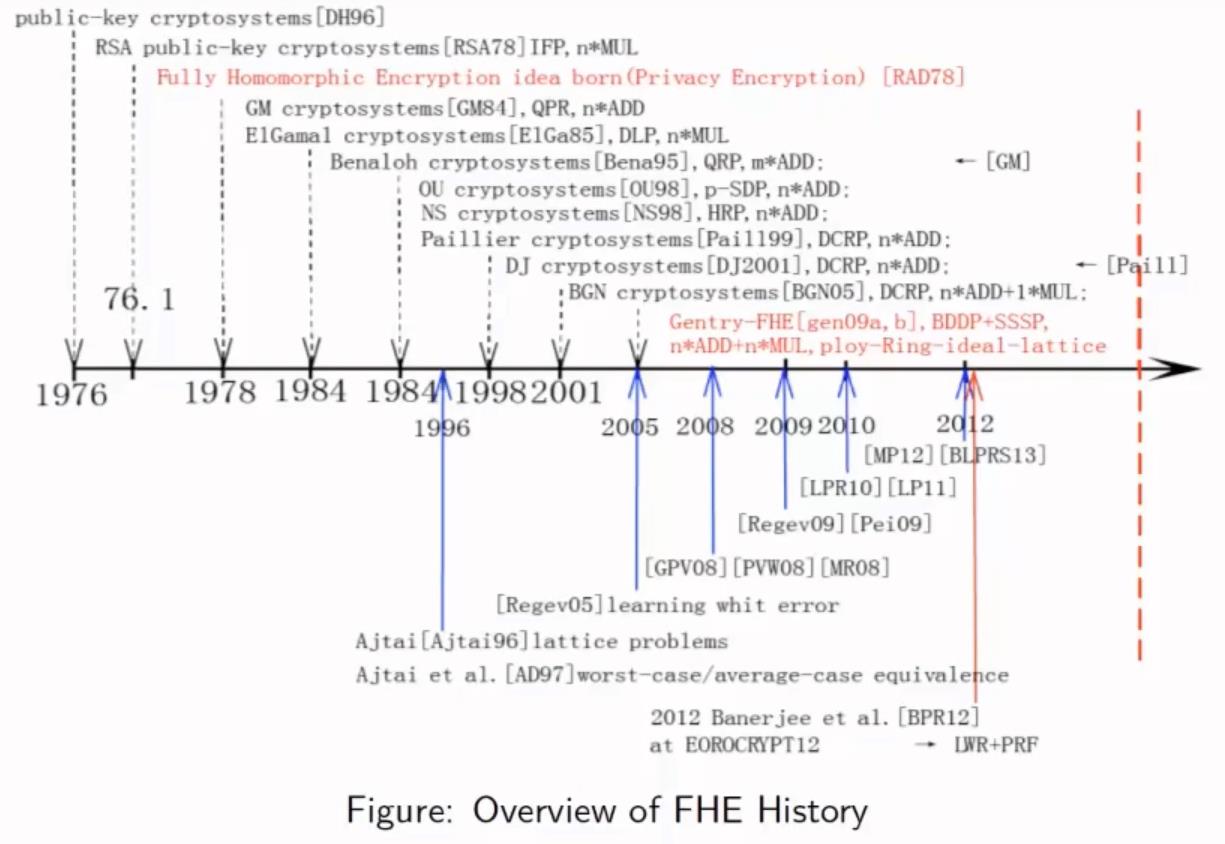
基于格上的加密

格

1、后量子密码候选

2、简单、快速、方便的并行

3、应用广泛（在同态加密、属性加密等使用）

基于格上的加密：

1、可以实现很好的线性操作

2、支持 “循环安全”：加密算法不依赖于密钥

LWE

利用“高斯消元法”在有限时间内可以解这个方程组（函数）：

加入噪声后，再使用高斯消元法就不能解：

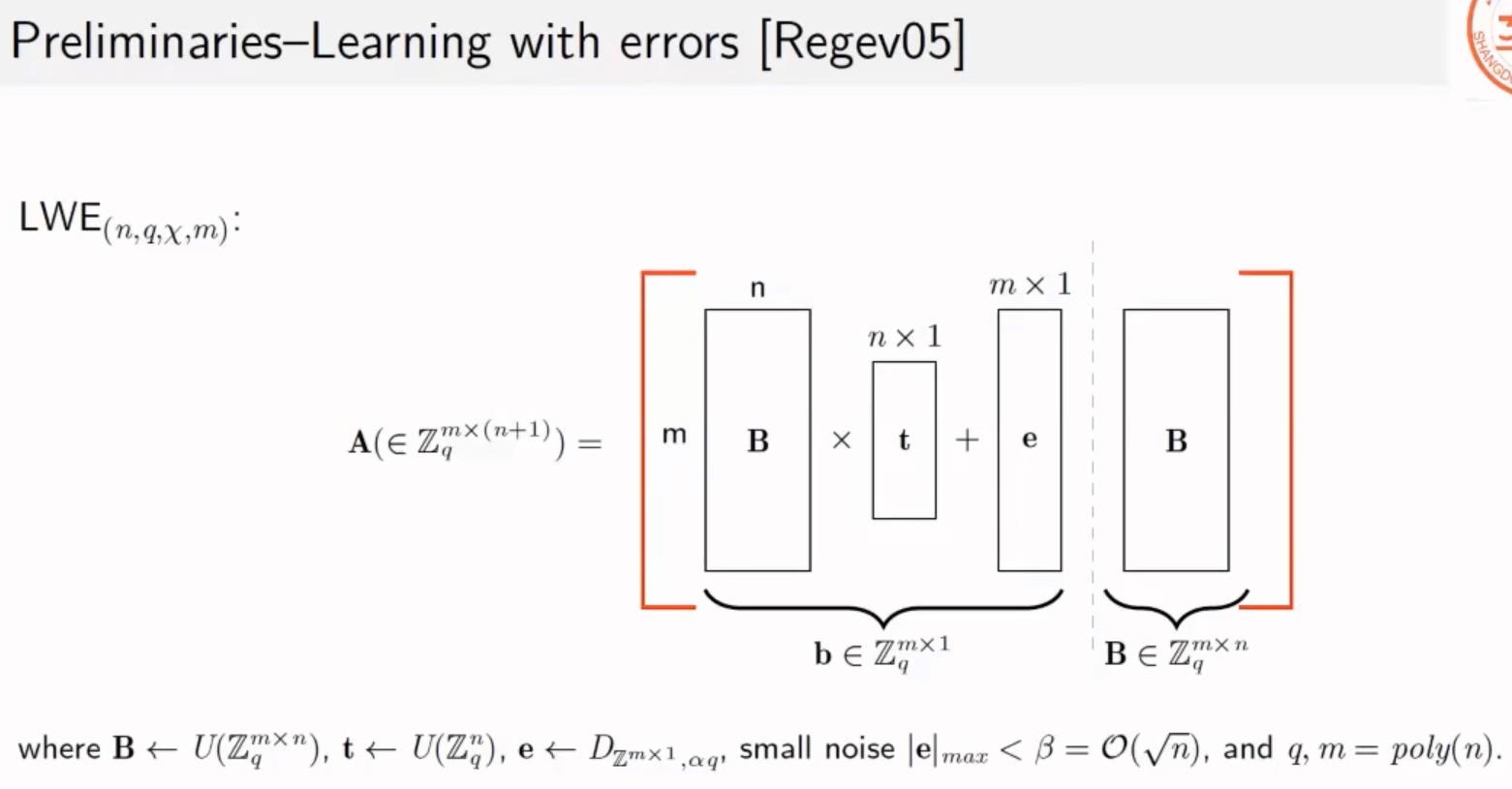
LWE可以分为两个版本：

1、SLWE：搜索问题（给出B、b、e难以计算出t）

2、DLWE：判定问题（给出B，b=Bt+e，难以区分b和一个随机取的一个向量）

RLWE

将运算从整数上转到环上，其他的没怎么变换

基于格上的公钥加密

Regev方案

不正式的表述：

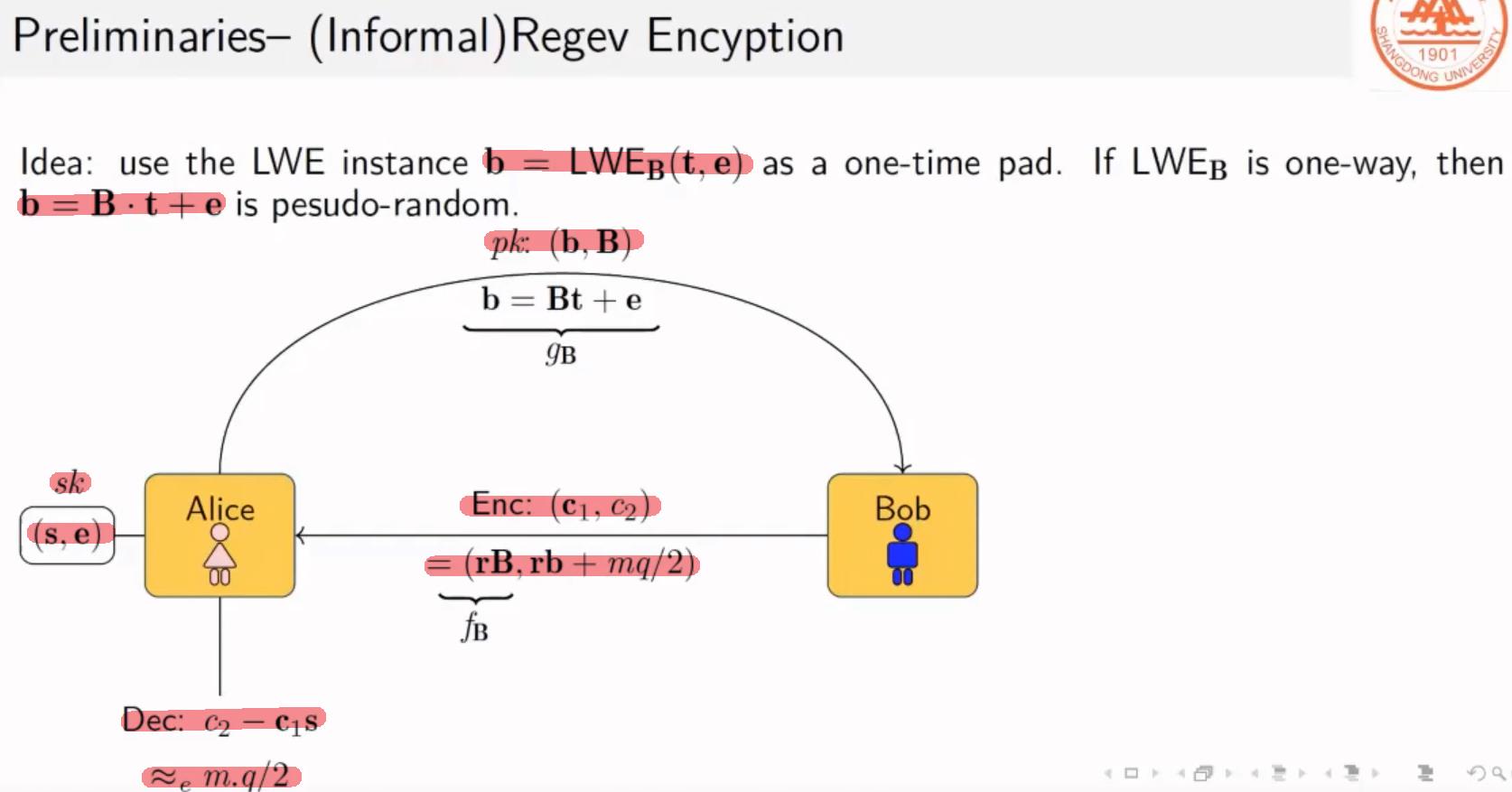
正式的表述：

对偶的Regev方案

和之前方案的不同之处就是：噪声出现的位置不同（噪音不是在公钥中，而是在密文上）

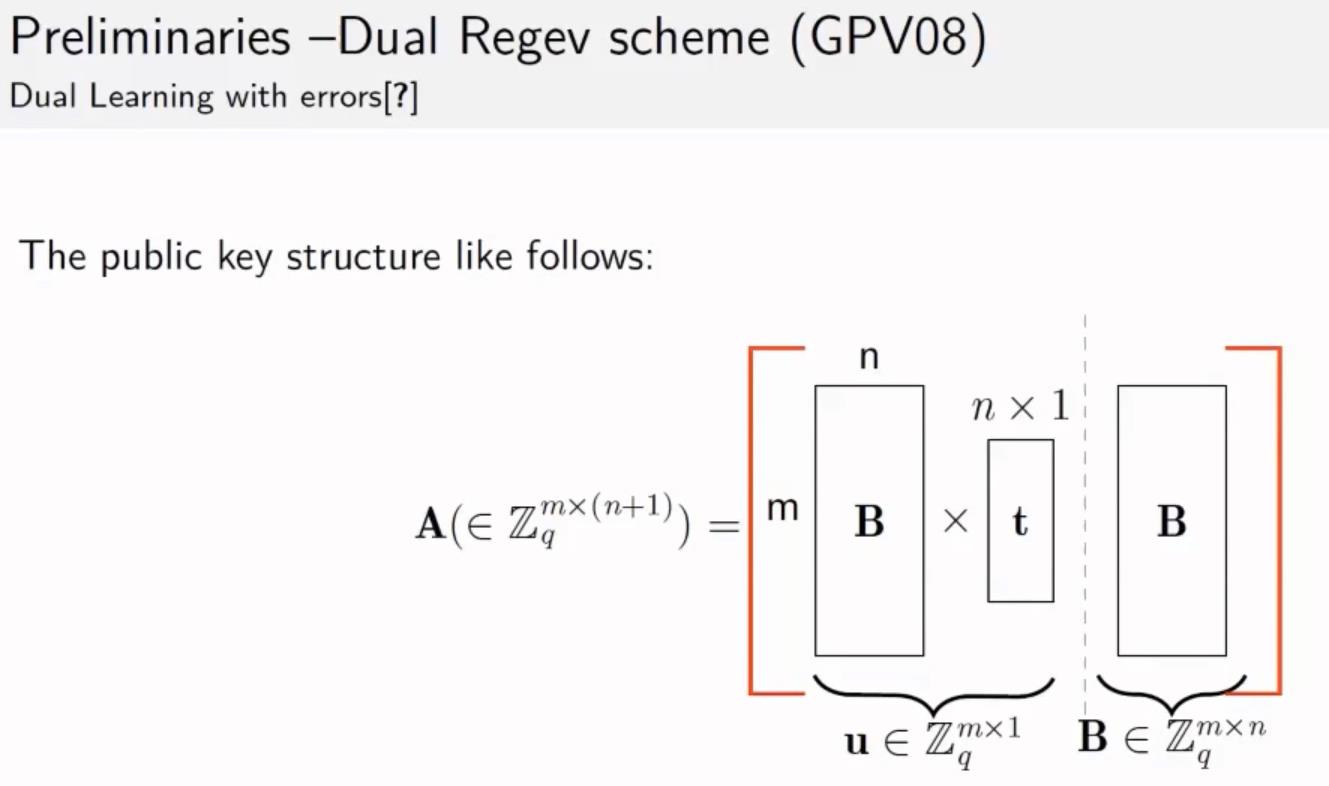
非正式表述：

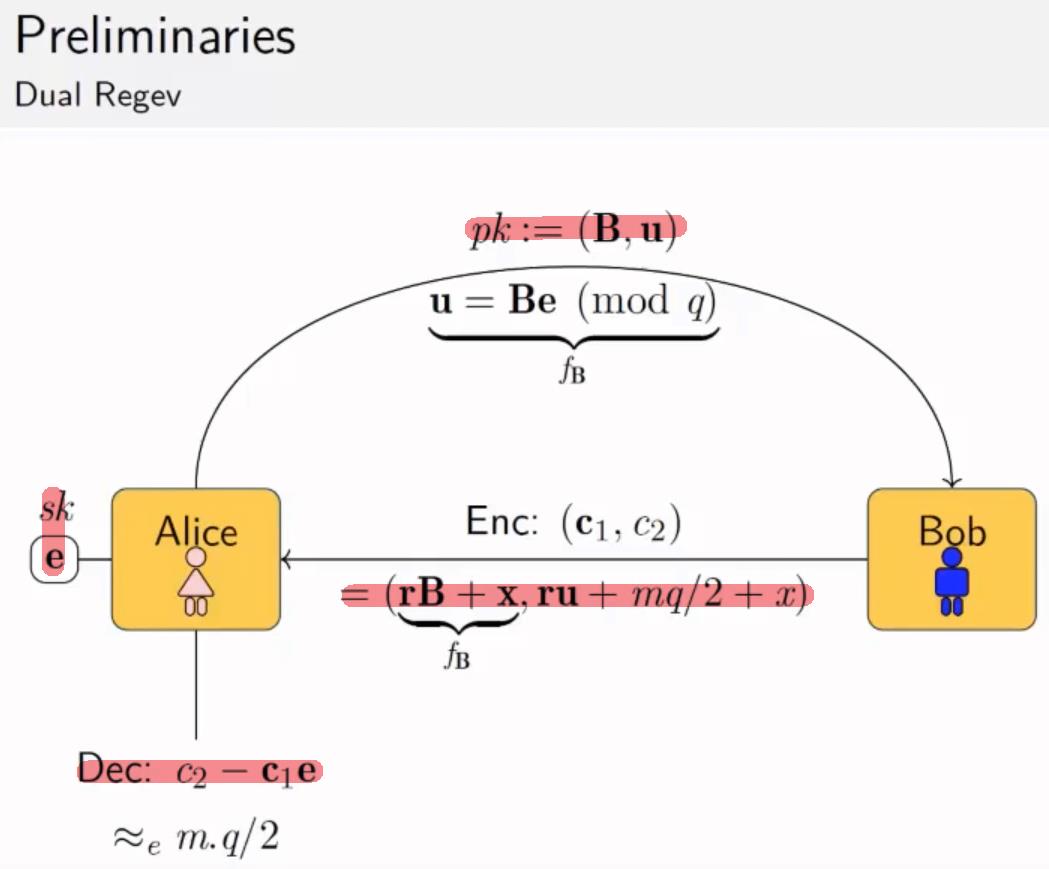
正式表述：

RLWE加密

基于RLWE加密方案，加密的消息mm可以是多比特，而基于LWE上的假设m只能是单比特：

全同态加密

既支持加法又支持乘法 

时间线

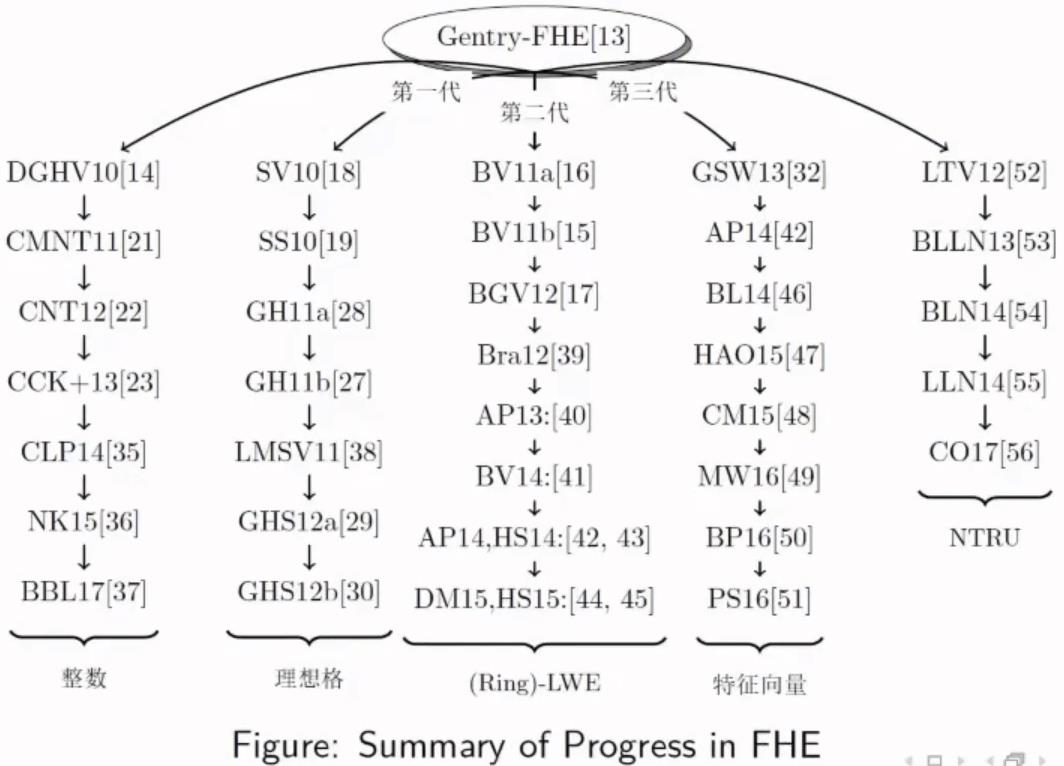
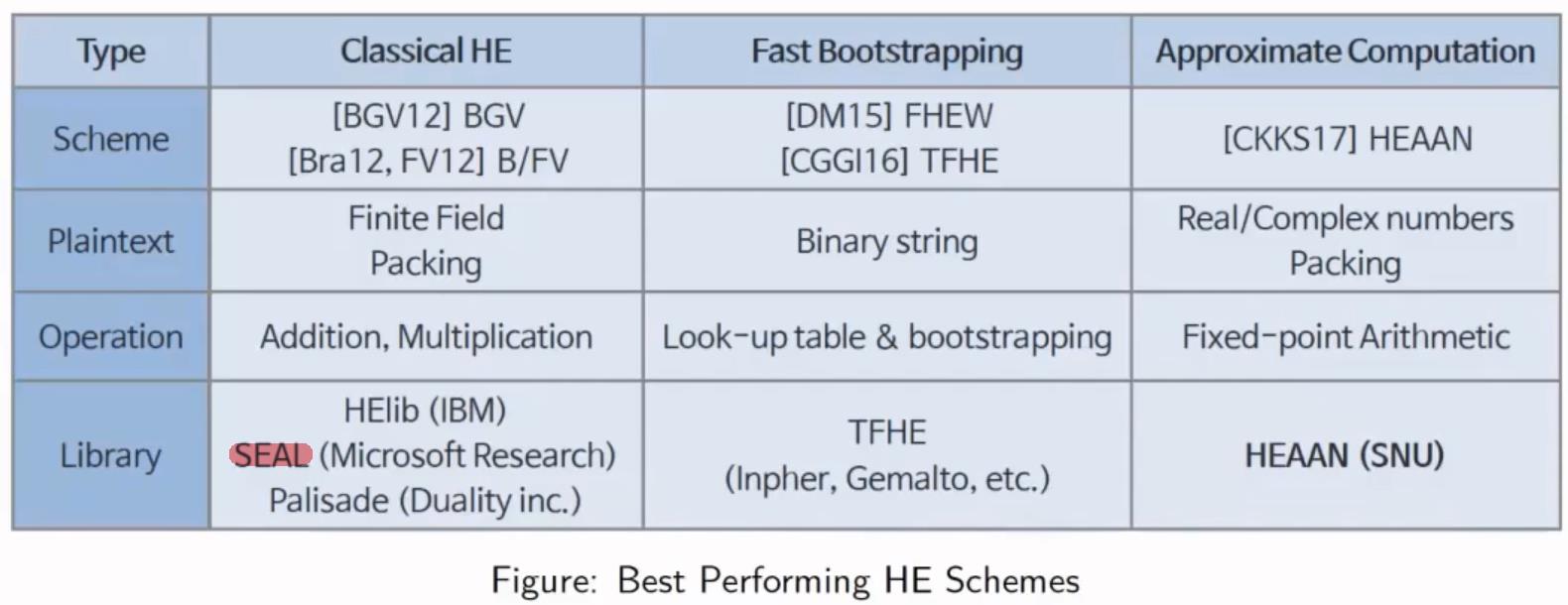
SEAL库：

1、实现了隐私计算求交协议

2、实现Bootstrapping

 三代FHE：

1、基于Gentry提出的基于理想格，使用自举（Bootstrapping）、重加密技术实现的FHE

2、基于LWE和RLWE，使用重线性化（relinearization）、模交换（module switch）、密钥交换（Key Switch）约减噪音、降维，例如：BV11、BGV、BFV，Bra等

3、运算不是向量之间运算，而是矩阵之间运算，不使用密钥交换技术降维，例如：GSW，CKKS等

BV11

基于LWE的方案：

其中密文乘法运算出现密文维数膨胀问题，这里使用密钥交换（Key Switch）技术降维：

密钥交换技术是较为成熟的降维技术

基于RLWE的方案：

举个栗子：

GSW

具体参考：GSW13

FHE的应用

1、不可区分性混淆

一个程序混淆后，仍然可以计算

2、相关难解问题

给出R(x,H(x))难以求x

3、同态加密的机器学习

4、安全多方计算

基于门限的全同态加密：结合秘密共享技术

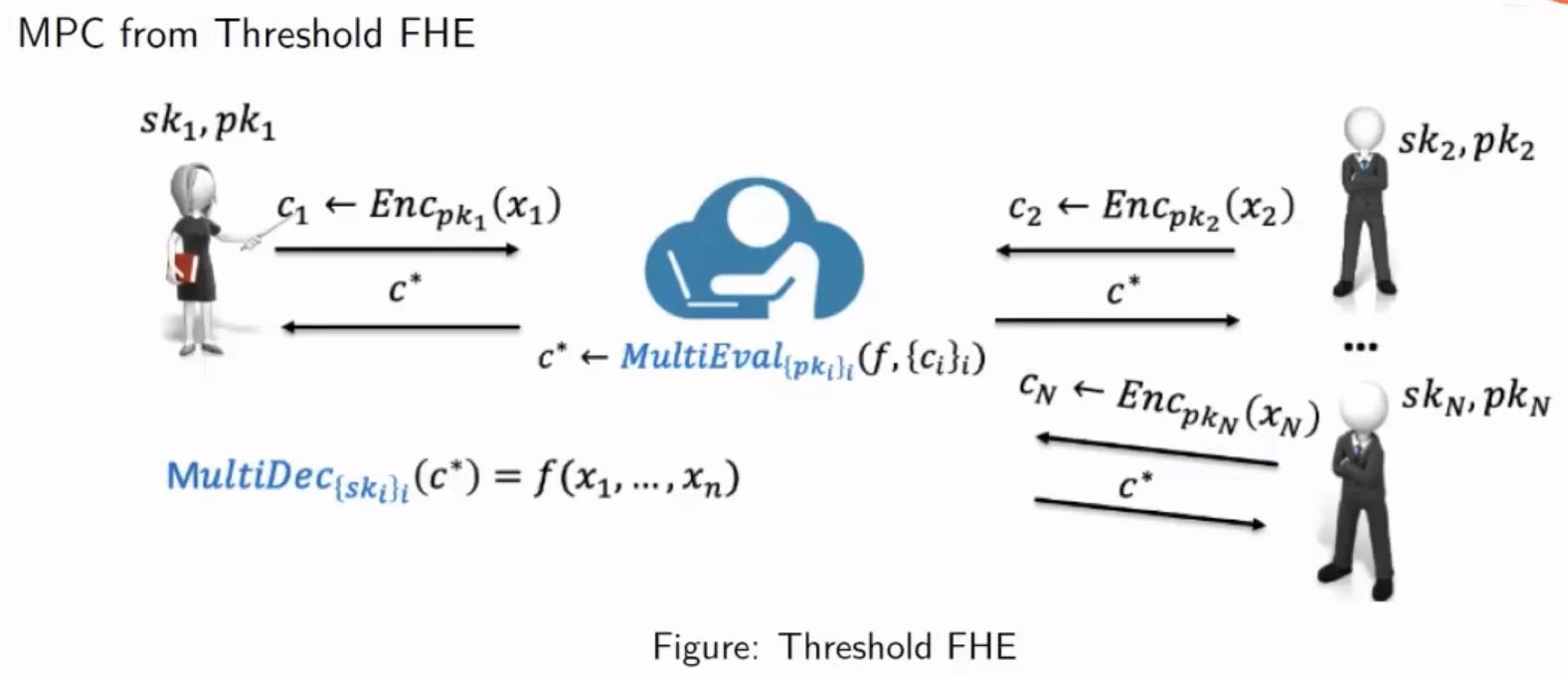
1、参与方通过秘密共享的方式将自己的私钥切分，  然后将相应的切分后份额广播出去；对方收到别人广播的私钥信息后，就会重构自己的私钥

2、参与方用自己的公钥加密加密信息，并将密文发送给第三方，第三方将所有的密文做同态运算，将求得的结果返回给各个参与方

3、参与方收到第三方的密文，只能使用自己重构的私钥去解密（拉格朗日多项式恢复明文）

Mutikey FHE方案：

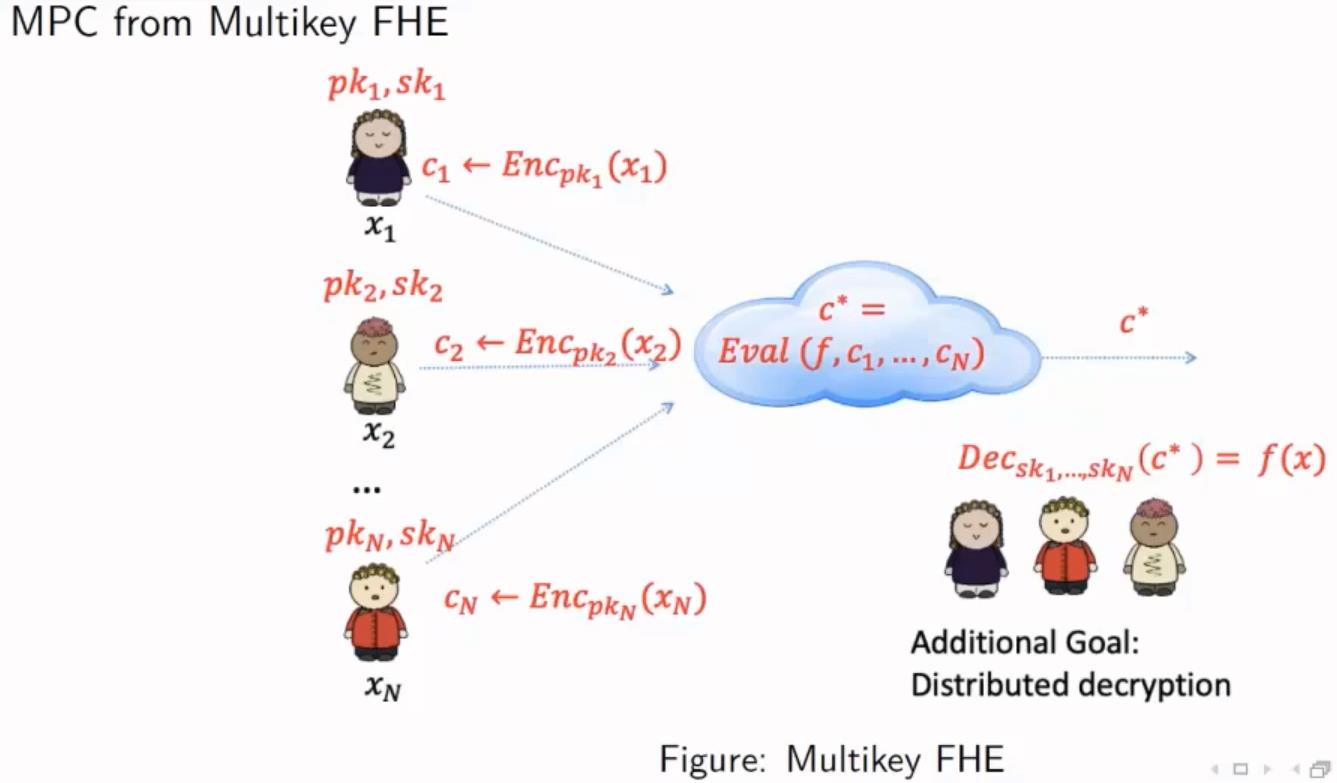
各个参与方都拥有各自的公私钥对，对第三方发来的密文，使用各自的私钥解密，只是其中明文的一部分，最后还需将所有参与方解密的明文部分重构，才能得到最终的明文

5、隐私计算集合求交

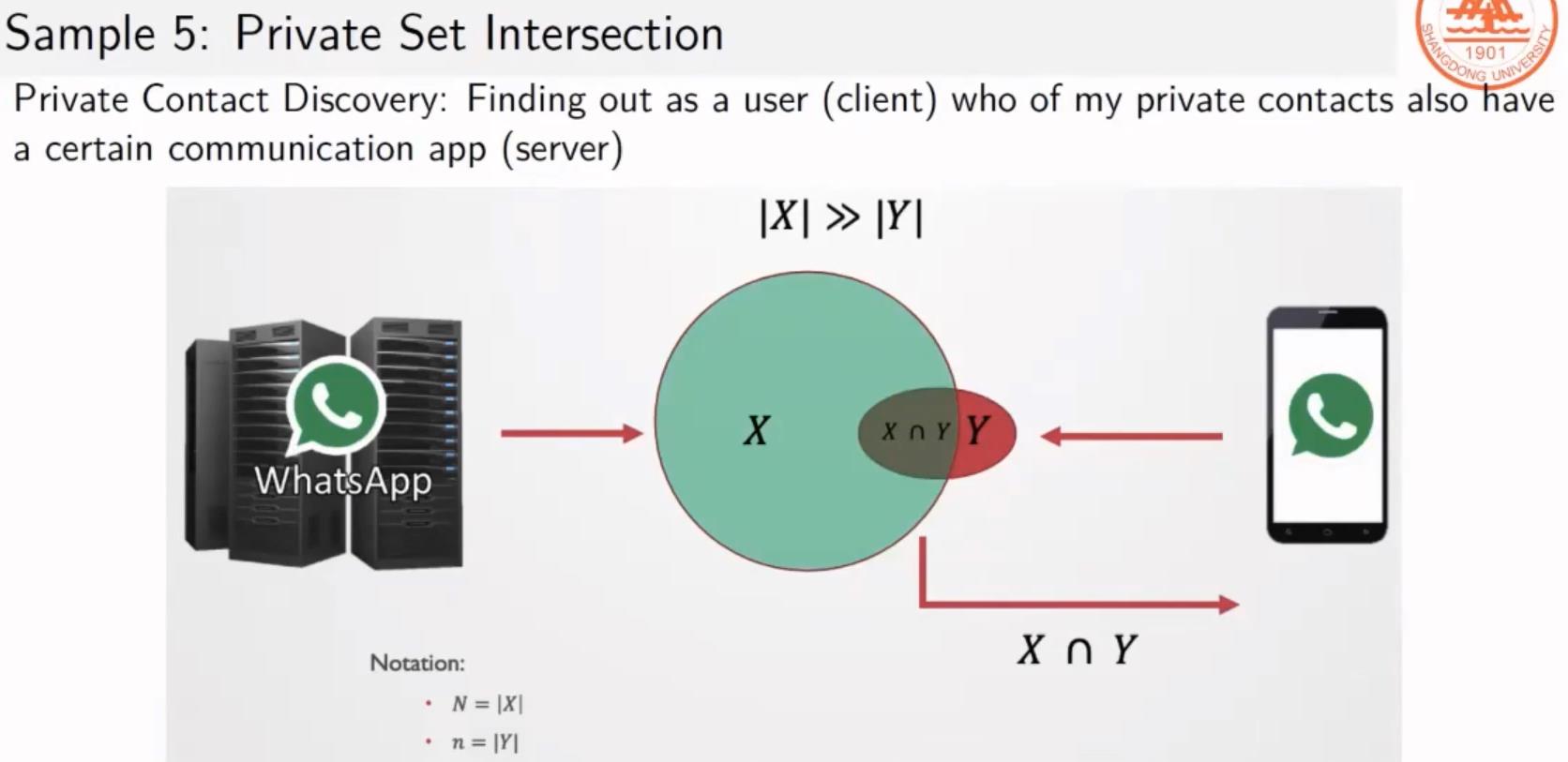
相容性检测：

明文和密文计算

 

总的来说，同态加密可与秘密共享、签名结合构造出新的应用

作者： Pam

出处： https://www.cnblogs.com/pam-sh/>

关于作者：网安在读

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出, 原文链接 如有问题， 可邮件（[e-mail]）咨询.