模板01背包问题

Posted 2023-05-27 MT默哥的博客

一个在旅途中的长者有一个最多能用\\(M\\)公斤的背包，现在有\\(n\\)件物品，它们的重量分别是\\(W1，W2，...,Wn\\),它们的价值分别为\\(C1,C2,...,Cn\\).求旅行者能获得最大总价值。

输入

• 第1行：两个整数，\\(M\\)（背包容量，\\(M\\le200\\)）和\\(n\\)（物品数量，\\(n\\le30\\)）；

• 第\\(2\\)至\\(n+1\\)行：每行两个整数\\(Wi\\),\\(Ci\\)，表示每个物品的重量和价值。

输出

• 仅一行，一个数，表示最大总价值。

样例

样例输入1

10 4
2 1
3 3
4 5
7 9

样例输出1

12

解析

好了，这是一个经典的01背包问题

做01背包问题只要记住一个公式：

d[j]=max(d[j],d[j-w[i]]+c[i])；

其中 d 数组表示当前容量可以装的最大价值，w[i] 是重量，c[i] 是价值。

在公式中，我们在装和不装中选一种：

1. 不装：就是当前的最大重量 d[j]

2. 装：先在当前容量 j 中给 当前重量 w[i] 预留一个位置 （d[j-w[i]]），然后在加上当前价值 c[i]

最后，用max函数在它们当中选大的那个就可以了

公式中有 i 有 j ，那么这是一个双重循环。

Code

#include <bits/stdc++.h>                 
using namespace std;
int v,n,d[2000],c[50],w[50];     //d数组的下标表示容量
int main()

	cin >> v >> n;      //v表示容量，n表示数量 
	for(int i=1;i<=n;i++)
		cin >>w[i] >>c[i];
	for(int i=1;i<=n;i++) 
		for(int j=v;j>=w[i];j--)
			//01背包中，第二重循环要倒序，从v到w[i]
		
			d[j]=max(d[j],d[j-w[i]]+c[i]);  //公式 
		
	cout << d[v]; //注意不是d[n] 
	return 0;

本文来自小默的博客，转载请注明原文链接：https://www.cnblogs.com/momotrace/p/01backpack-problem.html

模板背包

（死亡）

本文部分参照背包九讲（链接点这里）

先看三道题：

01背包，完全背包，混合背包

请记住这个题面：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

有相似题面的一系列一种组合优化的NP完全问题（附百度百科）就是背包问题。

背包的种类很多，大概（我会的）有01背包，完全背包，多重背包，分组背包。

从最基础的完全背包讲起。

完全背包

题面：

有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是ci，价值是wi。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

思路：

有F[u][v]用来存装了u种物品的背包里的最大价值。

对加入x个物品k的决策，有f[k][v]=f[k-1][v-c[k]*x]+w[k]*x

状态转移方程：f[k][v]=max{ f[k-1][v-c[k]*x]+w[k]*x (0<=k<=v/c[k]) }

时间复杂度O(VΣ(V/c))

空间复杂度O(NV)

 还有改进空间。。

先简单优化下：

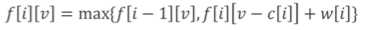
拿两个的状态可以从拿一个的转移而来，后面以此类推

（仔细观察还可以再优化的亚子？？）

优化代码大概长这样：

for(int i=1;i<=n;i++)
    {
        for(int j=w[i];j<=m;j++)
        f[j]=max(f[j-w[i]]+v[i],f[j]);
    }

完全背包就差不多了。。

画图来说就是这样的：
（二维）

 

 

再转成一维看一下：

 

这样就解释了为什么第二重循环要从小到大。 

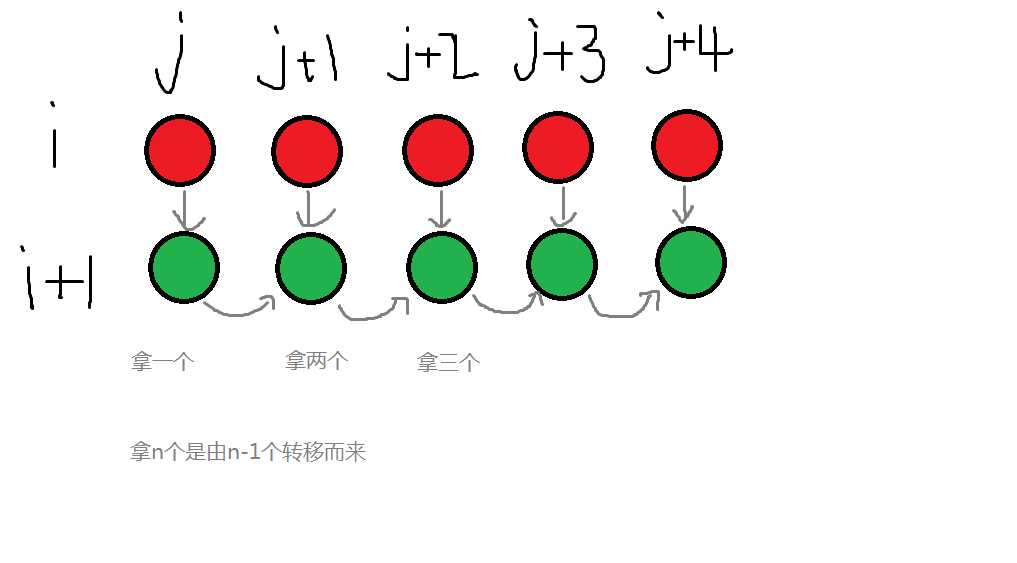
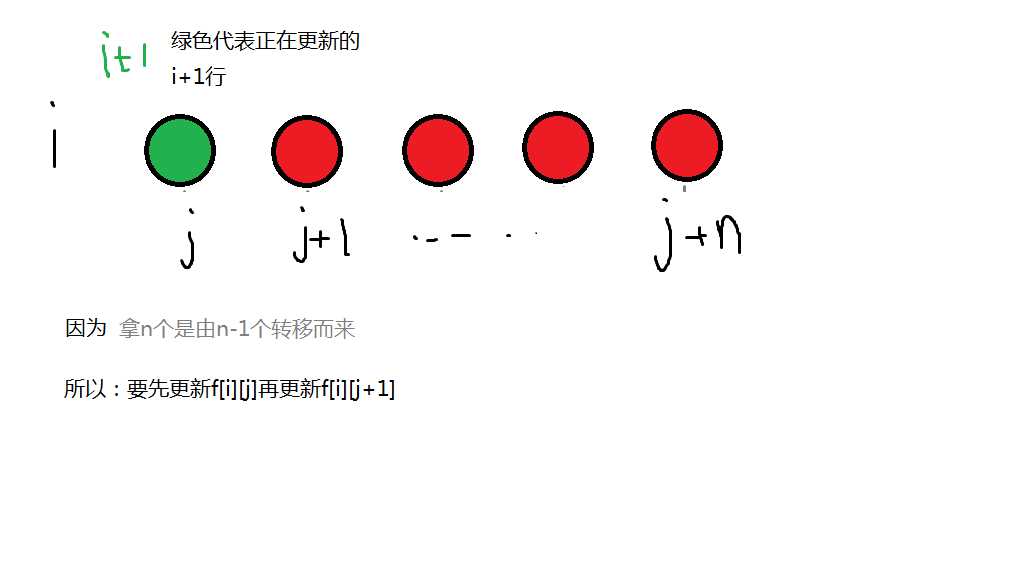
01背包

题面：

有N种物品和一个容量为V的背包，每种物品都只有1件可用。第i种物品的费用是ci，价值是wi。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

思路：

跟完全背包差不多，完全背包看懂了这个也就自然OK

连代码都差不多的亚子，但是还是有一点不一样

先看代码找不同：

 for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=w[i];j--)
        f[j]=max(f[j-w[i]]+v[i],f[j]);
    }

为什么内循环是从大到小？

画图解释一下：

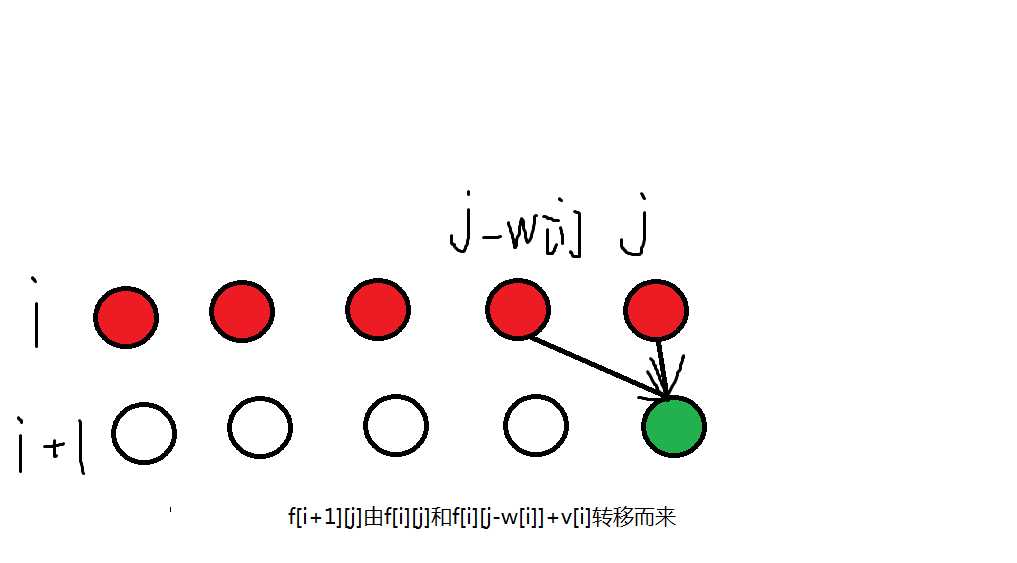
由此图可知：01背包依赖于已知前置位置

再改成一维的看看：

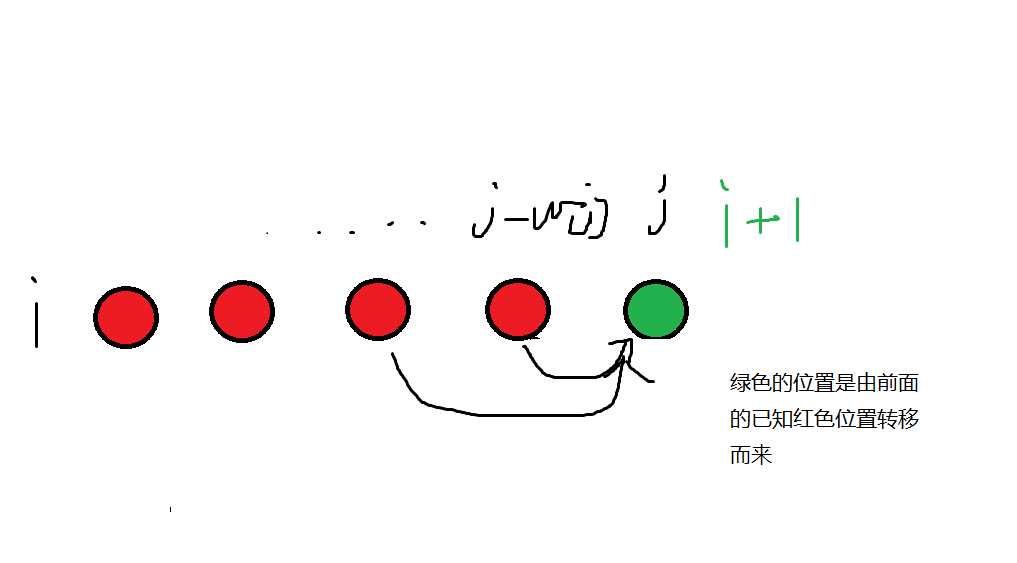
所以循环是从大到小

多重背包

题面：

有N种物品和一个容量为V的背包，每种物品都有n件可用。第i种物品的费用是ci，价值是wi。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

思路：

先介绍“二进制分组”

将一个自然数n分成m个数相加的形式，且1-n间的每一个数都可以被分成的m个数表示

例：

n=m1+m2+m3;

1-n中的所有数都可以用m1,m2,m3的和来表示

怎么实现就要用到万能的二进制了

将一个自然数n分成

n=a1*2¹+a2*2²+a3*2³+……+an*2ⁿ

这是会发现，这样并不能把所有自然数分完，特别是奇数，总会再剩一点。

所以设m=a1*2¹+a2*2²+a3*2³+……+an*2ⁿ

那么n就可以被表示成

n=a1*2¹+a2*2²+a3*2³+……+an*2ⁿ+(n-m)

而多重背包就是把n个物品二进制分组再重新处理它们的体积和价值，再用01背包即可。

代码：

for(int i=1;i<=n;i++)
    {
        int t=1;
        if(p[i]>1)
        {
            while(p[i]>t)
            {
                k++;
                w[n+k]=w[i]*t;
                v[n+k]=v[i]*t;
                p[n+k]=1;
                p[i]-=t;
                t*=2;
            }
            w[i]*=p[i];
            v[i]*=p[i];
            p[i]=1;
        }
    }
     
    for(int i=1;i<=n+k;i++)
    {
        if(p[i]==1)
        {
            for(int j=m;j>=w[i];j--)
            {
            f[j]=max(f[j],f[j-w[i]]+v[i]);
            }
        }

看一道例题：（点击收获RP++）

就很简单。。01背包就可以解决

AC代码：

#include<iostream>
#include<cstdio>
using namespace std;
int v,c,n;
int w[10001],f[10001],p[10001];//
bool vis[10001];
int main()
{
    scanf("%d%d%d",&v,&n,&c);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&w[i],&p[i]);
    }
//    f[0]=-0x7ffffff;
    for(int i=1;i<=n;i++)
    {
        for(int j=c;j>=p[i];j--)
        {
        
            f[j]=max(f[j],f[j-p[i]]+w[i]); 
        }
    }
    for(int i=1;i<=c;i++)
    {
        if(f[i]>=v)
        {
        printf("%d",c-i);
        return 0;
        }
        
    }
    printf("Impossible");
    return 0;
}

（RP++!）