图的相关知识
Posted qjwxlj
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图的相关知识相关的知识,希望对你有一定的参考价值。
图与之前学习的数据结构不同的地方在于他更加注重数据与数据之间的关系,他又顶点和边构成.图的最经常应用应该是人与人的好感度社交关系的应用.每个人是一个定点,每条边是人与人之间的亲密度.
图分为有向图和无向图,无向图是相互之间的关系,有向图是单方面之间的关系.完全图指图中任意两个顶点都至少有一条边相连.
连通图:有一个顶点出发可以访问所有顶点的图被叫做连通图,强连通图:如果对于每一对vi、vj,vi≠vj,从vi到vj和从vj到vi都存在路径,则称G是强连通图.
图的存储结构有很多种最常用的是邻接矩阵和邻接表........
数据结构学习笔记——图的基本知识
目录
一、图的结构
- 树和图一样,也是一种
非线性结构,线性结构中的数据元素之间是“一对一”的关系,树形结构中的数据元素之间是“一对多”的关系,而图中的数据元素之间是“多对多”的关系,每个数据元素可以有多个直接前驱和多个直接后继,即图的结构是网状结构。
注:图与线性表、树不一样,线性表、树可以为空表、空树,但图不能为空图。
二、图的定义
- 图是由一个非空的顶点集合V(
顶点集)和一个描述顶点之间关系——边的有限非空集合E(边集)所组成的一种数据结构,记为G=(V,E),其中图的顶点集V不一定为空,而图的边集E可以为空。
(一)有向图和无向图
按照图中的边是否有方向性,可以分为有向图和无向图。
1、无向图和无向完全图
无向图中每条边都没有方向,一般用圆括号“()”表示两个顶点之间的边,若边中带有数据信息,则称为权,(vi,vj)表示顶点vi和顶点vj之间的无向边。【带权的无向图称为无向网】

上图可表示为:
G=(V,E)
V= V1,V2,V3,V4
E= (V1,V2),(V1,V3),(V2,V1),(V2,V3),(V2,V4),(V3,V4)
若一个无向图中,若每个顶点都有一条边连接,则称为无向完全图,可知:
- ✨在一个含有n个顶点的无向完全图中,共有
n(n-1)/2条边。
例如,下面就是一个无向完全图,n=4,含有6条边:

2、有向图和有向完全图
有向图中每条边都有方向,一般用尖括号“<>”表示两个顶点之间的首尾关系,<vi,vj>表示从顶点vi到顶点vj的弧,同样,若弧中带有数据信息,也称为权。<vi,vj>其中第一项vi称为弧尾,第二项vj称为弧头,也称为顶点vi邻接到顶点vj。【带权的有向图称为有向网】

上图可表示为:
G=(V,E)
V= V1,V2,V3,V4
E= <V2,V1>,<V2,V3>,<V2,V4>,<V3,V1>,<V4,V3>
若一个有向图中,若每个顶点都有互相相反的两条弧连接,则称为有向完全图,可知:
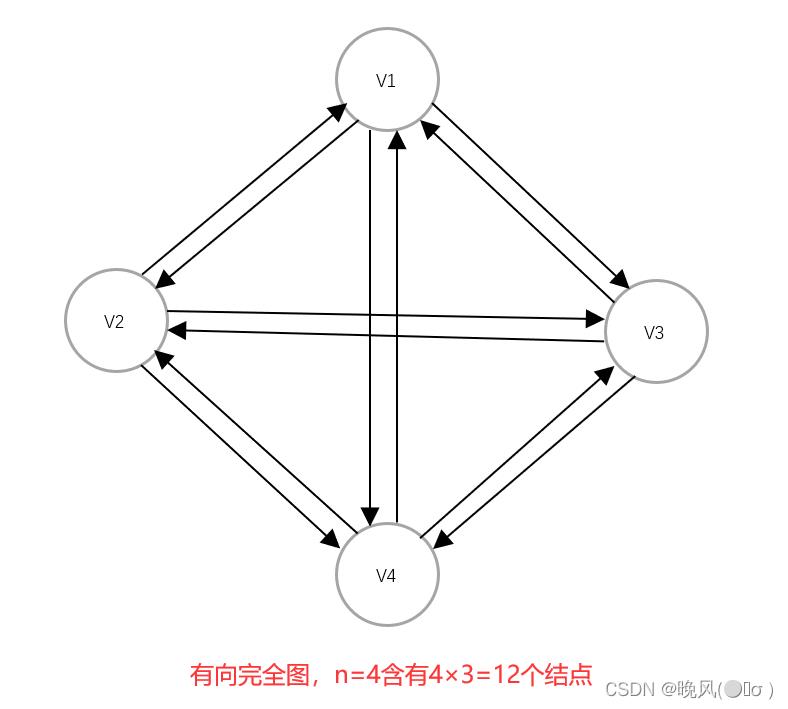
- ✨在一个含有n个顶点的有向完全图中,共有
n(n-1)条弧。
例如,下面就是一个有向完全图,n=4,含有12条弧,每个顶点都有相互的弧连接:
(二)度的概念
1、无向图的度
在无向图中,对于一个顶点,其边的个数称为该顶点的度,记为TD(v),例如,下面这个无向图中:
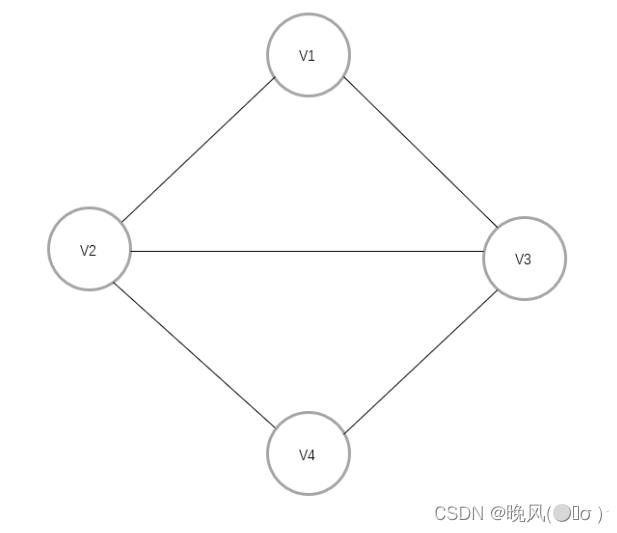
各结点的度为:
TD(V1)=2
TD(V2)=3
TD(V3)=3
TD(V4)=2
- ✨在一个无向图中,所有顶点的度之和等于所有边数的两倍。
例如,对于上面这个图,其顶点度之和为2+3+3+2=10,该图边的个数为5,故10=2×5。
2、有向图的度
在有向图中,对于一个顶点,该结点的度等于顶点的入度+顶点的出度,
该结点的弧头数目称为入度,记为ID(v);结点的弧尾数目称为出度,记为OD(v),即TD(v)=ID(v)+OD(v):

例如,下面这个有向图中:

各结点的度为:
ID(V1)=2,OD(V1)=0
ID(V2)=0,OD(V2)=3
ID(V3)=2,OD(V3)=1
ID(V4)=1,OD(V4)=1
TD(V1)=ID(V1)+OD(V1)=2+0=2
TD(V2)=ID(V2)+OD(V2)=0+3=3
TD(V3)=ID(V3)+OD(V3)=2+1=3
TD(V4)=ID(V4)+OD(V4)=1+1=2
- ✨对于一个含有n个顶点有向图,每个顶点的度最大可达
2(n-1),另外所有顶点的入度之和等于所有顶点出度之和。
例如,对于上面这个有向图,其所有的顶点的入度之和为2+0+2+1=5,所有的顶点出度之和为0+3+1+1=5,它们是相等的。
- ✨对于一个有n个结点,e条边的图,顶点vi的度与顶点的个数以及边的数目满足以下关系:
∑ i = 1 n T D ( v i ) = 2 e \\sum_i=1^n TD(v_i)=2e i=1∑nTD(vi)=2e
例、若无向图G有23条边,度为4的顶点有5个,度为3的顶点有4个,剩下都是度为2的顶点,求图G中顶点数目。
解: 由 ∑ i = 1 n T D ( v i ) = 2 e ,可知, e = 23 ,即 由\\sum_i=1^n TD(v_i)=2e,可知,e=23,即 由i=1∑nTD(vi)=2e,可知,e=23,即
设剩下度为2的结点数目为x,则,4×5+3×4+2x=2×23=46,
所以得到x=7,故5+4+7=16,共16个结点。
例、已知无向图G含有16条边,其中度为4的顶点个数为3,度为3的顶点个数为4,其他顶点的度均小于3,求图G所含的顶点个数至少为____________。
解:由于其他顶点的度均小于3,当剩余顶点的度为2时,此时顶点的个数最少,
可设剩下度为2的结点数目为x,则4×3+3×4+2x=16×2=32,
得到x=4,故3+4+4=11,图G所含的顶点个数至少为11。
(三)路径、路径长度和简单路径
路径,即一个顶点到另一个顶点经过的顶点序列,路径上边或弧的数目称为路径长度;若顶点序列中的各顶点不同,则称这样的路径称为简单路径。

这个无向图中,顶点V2到顶点V3的路径有:
V2→V1→V3,路径长度为2
V2→V4→V3,路径长度为2
V1→V3,路径长度为1
另外,例如V2→V1→V3就是一个简单路径,其顶点序列中的各顶点不同。
(四)回路和简单回路
在一个路径中,若起始结点与结束结点相同,则称该路径为一个回路或环;另外,除了第一个结点和最后一个结点外,若顶点序列中的各顶点不同,则称这样的路径称为简单回路
例如,上面这个无向图中,V2→V1→V3→V2是一个回路,V2→V3→V4→V2也是一个回路,同样,V2→V1→V3→V4→V2也是一个回路,这些回路中,除了第一个结点和最后一个结点外,若顶点序列中的各顶点不同,它们也都是简单回路。
- ✨若一个图有n个顶点,且有大于n-1条边,则该图一定有回路。

(五)距离
若从一个顶点到另一个顶点之间的最短路径存在,这称该路径的长度为该结点到另一个结点的距离,若两个结点之间不存在路径,则记距离为无穷(∞ )。
三、图的相关知识
(一)简单图、多重图
若一个图满足以下条件,则称为简单图:
1、没有重复的边;
2、不存在顶点到其自身的边;
反之,则为多重图。
例如,以下都是简单图:

(二)子图
对于两个图G1=(V1,E2)和G2=(V1,E2),若V2是V1的子集,且E2是E1的子集,则称G2是G1的子图,另外若有V(G2)=V(G1)的子图G2,则称其为G1的生成子图。

例如上面,G2是G1的子图。
(三)连通图和强连通图
连通图指的是无向图,强连通图指的是有向图:
- ✨一个含有n个顶点的图,它最少有1个连通分量,最多有n个连通分量。
1、无向图——连通图、连通分量
在无向图中,若一个顶点到另一个顶点存在路径,则称这两个结点是连通的。若无向图中任意两个结点都是连通的(任意两个结点之间有路径),则称该图为连通图,否则为非连通图;无向图的极大连通子图称为连通分量。
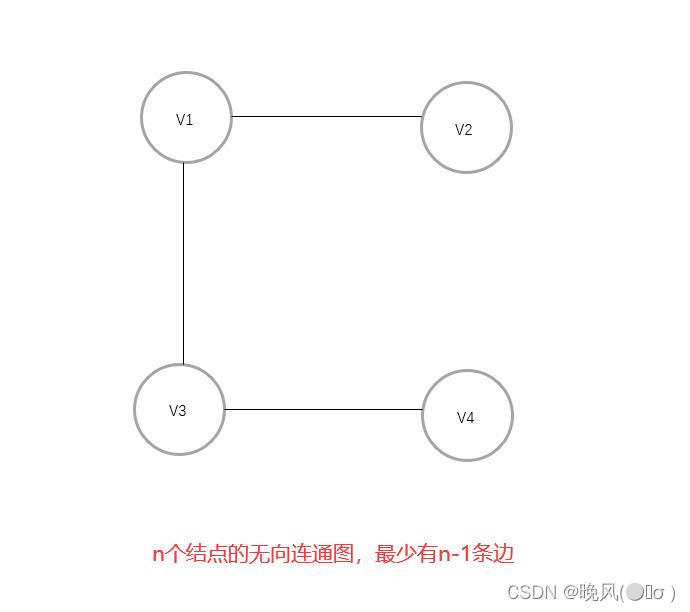
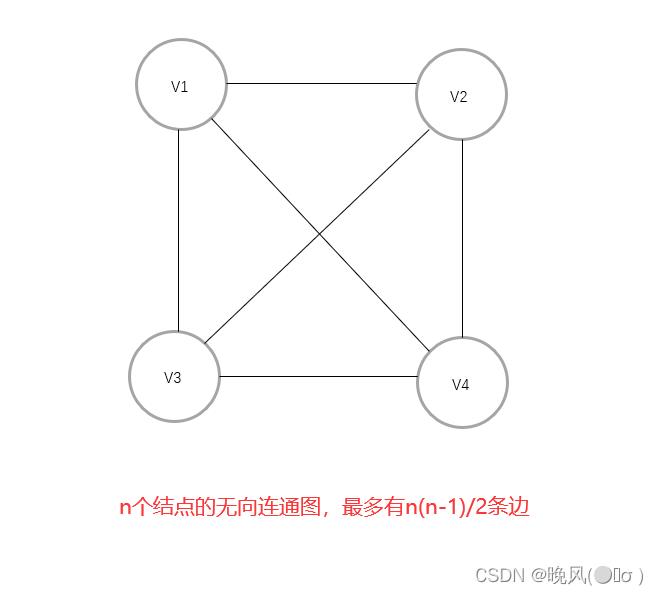
- ✨若一个含有n个顶点的无向连通图,构成一棵树时图中边数最少,有
n-1条边;当无向完全图时图中边数最多,有n(n-1)/2条边。
例、具有6个顶点的无向图中,当至少有_________条边时能确保是一个连通图。
解:可知,由于求的是至少而不是最少,如果是最少,即为一棵树时边最少,即n-1=5。
先考虑5个结点,5个结点构成一个无向完全图,需要5×4/2=10条边,此时是连通的,
再加上一个顶点,只需加上1条边,即可与该无向完全图连通,即需要10+1=11条边。
例、一个具有28条边的非连通无向图至少有________个顶点。
解:考虑为由一个含有n个顶点的无向完全图和一个单独的顶点构成非连通无向图,
无向完全图中共n(n-1)/2条边,n(n-1)/2=28,
即为n=8最大边数,这样结点数最少,再加上单独的一个顶点故至少有8+1=9个顶点。
- ✨若一个无向图为连通图,则其连通分量只有一个,为该图自身,而非连通的无向图可以有多个连通分量。
例如下面,这是一个非连通的无向图G,并不是任意两个结点都是连通的:

可知该无向图有两个连通分量G1、G2:

2、有向图——强连通图、强连通分量
在一个有向图中,任意两个不同的顶点都存在相互之间的路径,则称为强连通图,其中任意顶点到其他顶点都有路径,但不一定有弧;同样,有向图的极大强连通子图称为强连通分量。
另外,有向完全图一定是强连通图,但强连通图不一定是有向完全图,因为有向完全图中每个顶点都有互相相反的两条弧连接。

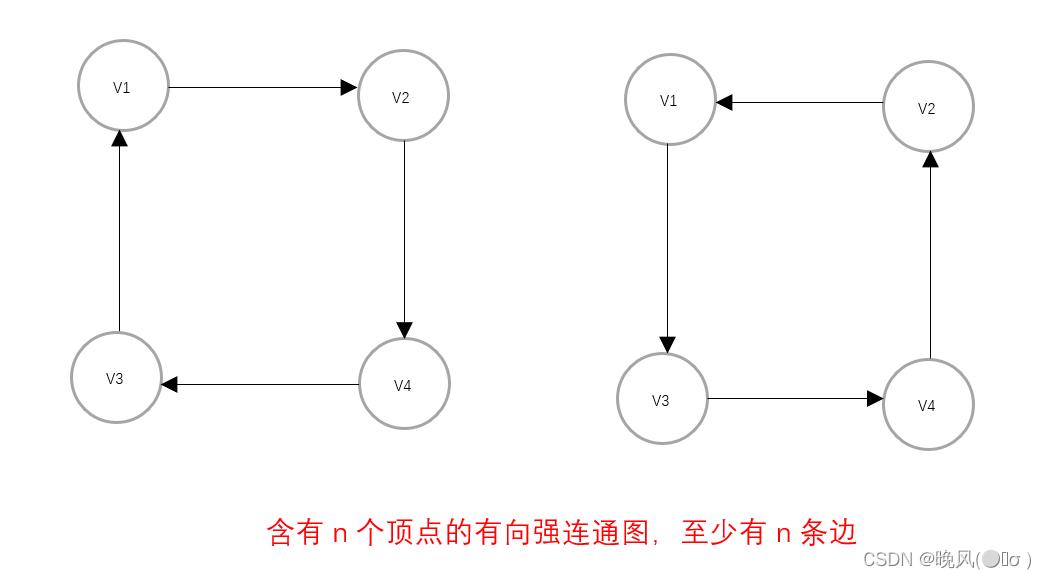
- ✨一个含有n个顶点的有向强连通图,当构成一个回路时图中边数最少,有
n条边(如下);当为有向完全图时图中边数最多,有n(n-1)条边(如上)。
- ✨若一个有向图为强连通图,则其强连通分量只有一个,为该图自身,而非强连通的有向图可以有多个强连通分量。
例如下面,这是一个非强连通的有向图G,并不是任意两个结点都是连通的:

可知该有向图有两个连通分量G1、G2:

(四)稀疏图、稠密图
- 一个图G=(V,E),边的个数为e,n为顶点数,则当e<nlog2n,则称为稀疏图,反之则为稠密图。
四、生成树、生成森林
在一个连通图中,若该图的一个子图是一棵包含该图所有顶点的树,则称为该图的生成树,即包含图中所有结点的一个极小连通子图,若该图含有n个顶点,则生成树含有n-1条边。
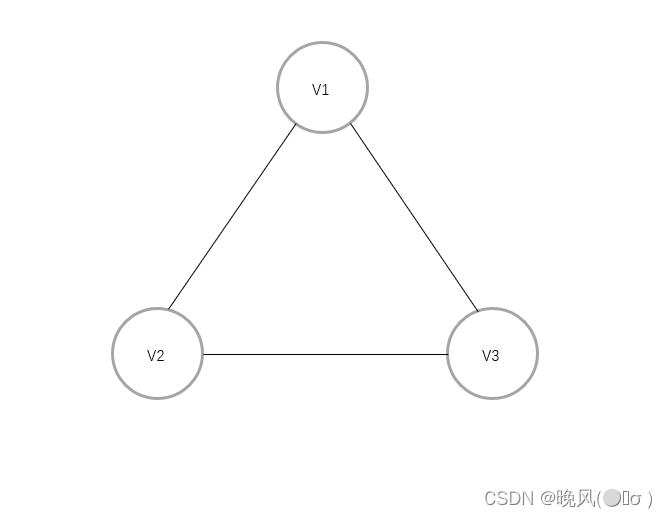
- ✨若由n个顶点构成一个回路(环)的图,由于它的生成树只要去掉一条边即可形成一棵生成树,故其生成树的数目为n。
例如,下面这个由3个顶点构成的图,它形成了一个回路:

其生成树的数目为3,如下:

在非连通图中,由于非连通的无向图可以有多个连通分量,连通分量的生成树可以构成一个该非连通图的生成森林。
以上是关于图的相关知识的主要内容,如果未能解决你的问题,请参考以下文章